Hoe Bereken Je De Inhoud Van Een Cilinder

Ken je dat? Je staat in de winkel, twee blikken soep in je hand. De ene is hoger en smaller, de andere lager en breder. Welke bevat nu daadwerkelijk meer soep? Of misschien moet je een nieuwe watertank installeren en wil je precies weten welke capaciteit je nodig hebt. In beide gevallen is het handig om de inhoud van een cilinder te kunnen berekenen! Gelukkig is het makkelijker dan je denkt. Deze gids loodst je door de formule en laat je zien hoe je het in de praktijk toepast.

Wat is een Cilinder?

Laten we beginnen met de basis. Een cilinder is een driedimensionale vorm met twee identieke, parallelle cirkelvormige vlakken (de 'bodem' en het 'deksel') die met elkaar verbonden zijn door een gebogen oppervlak. Denk aan een blikje frisdrank, een rol keukenpapier, of een pijp. Allemaal cilinders!

Het is belangrijk om de componenten van een cilinder te begrijpen:

Radius (r): De straal van de cirkelvormige basis. Het is de afstand van het middelpunt van de cirkel tot een punt op de rand.
Hoogte (h): De afstand tussen de twee cirkelvormige bases.

De Formule voor de Inhoud van een Cilinder

Nu komt het belangrijkste: de formule! De inhoud van een cilinder bereken je met de volgende formule:

Volume (V) = π * r² * h

Waar:

V = Het volume (de inhoud) van de cilinder.
π (pi) = Een wiskundige constante, ongeveer gelijk aan 3.14159. Je kunt meestal 3.14 gebruiken voor praktische berekeningen.
r = De radius (straal) van de basiscirkel.
h = De hoogte van de cilinder.

Laten we dit even ontleden. r² betekent 'radius in het kwadraat', dus je vermenigvuldigt de radius met zichzelf. En π * r² is niets anders dan de oppervlakte van de cirkelvormige basis! Dus eigenlijk zeg je: "de oppervlakte van de basis vermenigvuldigd met de hoogte". Dat is best logisch, toch?

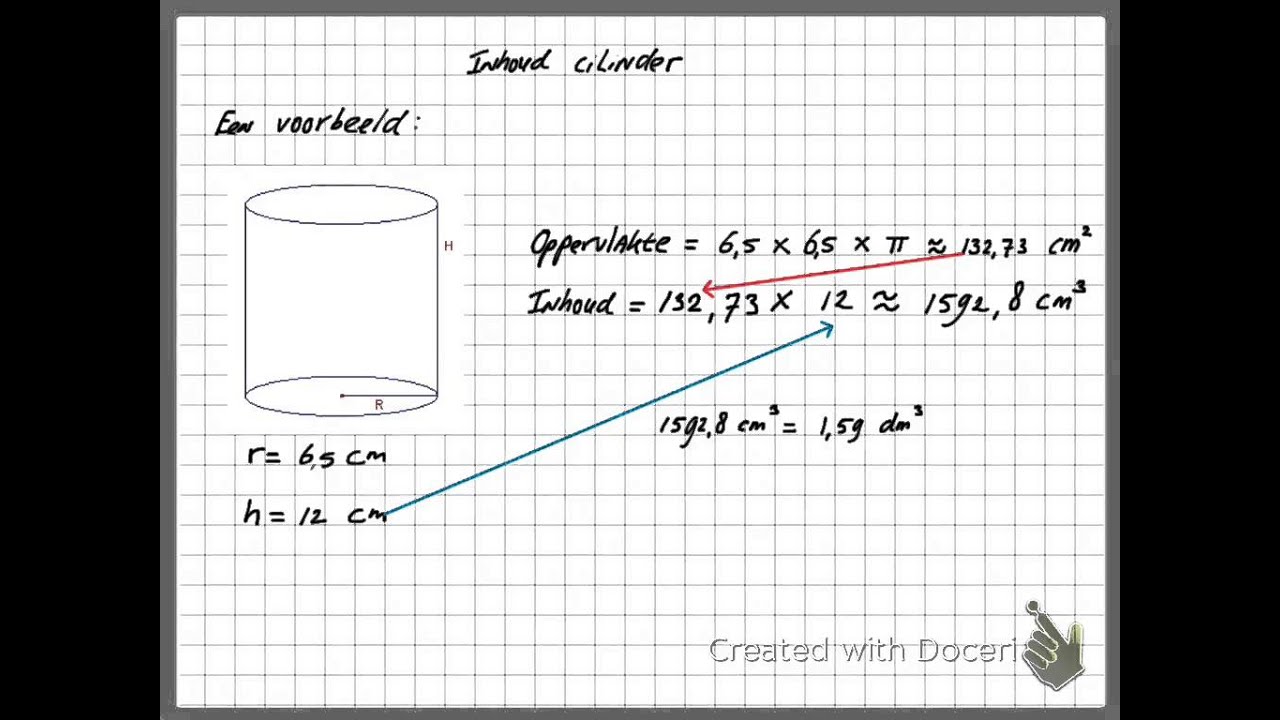
Stap-voor-Stap Berekening: Een Praktisch Voorbeeld

Oké, genoeg theorie. Tijd voor een voorbeeld. Stel, we hebben een cilinder met een radius van 5 cm en een hoogte van 10 cm. Hoe berekenen we de inhoud?

Bepaal de radius (r): In dit geval is r = 5 cm.
Bepaal de hoogte (h): In dit geval is h = 10 cm.
Bereken de oppervlakte van de basis (π * r²): 3.14 * 5² = 3.14 * 25 = 78.5 cm²
Bereken het volume (V = π * r² * h): 78.5 cm² * 10 cm = 785 cm³

Dus, de inhoud van de cilinder is 785 kubieke centimeter (cm³). Belangrijk: De eenheid van het volume is altijd in kubieke eenheden (cm³, m³, liter, etc.).

Waarom is dit Belangrijk? Toepassingen in het Dagelijks Leven

Je denkt misschien: "Wanneer heb ik dit nou nodig?". Maar geloof het of niet, de berekening van de inhoud van een cilinder is verrassend handig in verschillende situaties:

Koken en bakken: Recepten geven vaak de inhoud van een bakvorm aan.
Tuinieren: Bereken de inhoud van een bloempot of een regenton.
Bouw: Bereken de hoeveelheid beton die nodig is voor een cilindervormige fundering.
Logistiek: Bereken de capaciteit van vaten en containers.
Aankoopbeslissingen: Zoals in het voorbeeld aan het begin, bepalen welke verpakking meer product bevat.

Denk ook aan de medische wereld. Scans zoals MRI's en CT-scans gebruiken cilindrische modellen om organen te visualiseren en hun volume te schatten. Deze volumebepalingen helpen bij het diagnosticeren en volgen van aandoeningen. "Medische beeldvorming maakt intensief gebruik van volumetrische analyses gebaseerd op cilindrische benaderingen," aldus Dr. Anna de Vries, radioloog aan het Erasmus MC.

Tips en Trucs voor Nauwkeurige Berekeningen

Hier zijn een paar tips om ervoor te zorgen dat je de inhoud van een cilinder nauwkeurig berekent:

Gebruik de juiste eenheden: Zorg ervoor dat je alle metingen in dezelfde eenheden hebt (bijvoorbeeld allemaal in centimeters of meters). Als je verschillende eenheden hebt, converteer ze dan eerst!
Wees nauwkeurig met de radius: De radius is gekwadrateerd in de formule, dus een kleine fout in de radius kan een grote invloed hebben op het eindresultaat. Meet de diameter van de cirkel en deel deze door twee om de radius te vinden als je de radius zelf niet direct kunt meten.
Gebruik een rekenmachine: Vooral als je met complexe getallen werkt, kan een rekenmachine je helpen om fouten te voorkomen. Veel rekenmachines hebben een pi-knop, wat handig is!
Controleer je antwoord: Is je antwoord logisch? Een kleine cilinder kan geen enorm volume hebben. Gebruik je gezond verstand!

Alternatieve Methoden voor Lastige Situaties

Soms is het lastig om de radius of hoogte direct te meten. Hier zijn een paar alternatieve methoden:

* Waterverplaatsing: Als je een cilinder hebt die je kunt vullen met water, kun je de inhoud bepalen door de hoeveelheid water te meten die het verplaatst wanneer je de cilinder erin dompelt. Deze methode is vooral handig voor onregelmatige cilinders. * Benadering: Voor zeer grote cilinders, zoals opslagtanks, kan het soms praktischer zijn om het volume te benaderen door de cilinder op te delen in kleinere, beter meetbare secties.

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Er zijn een paar veelgemaakte fouten die mensen maken bij het berekenen van de inhoud van een cilinder. Hier zijn de meest voorkomende en hoe je ze kunt vermijden:

De diameter verwarren met de radius: Dit is een veelgemaakte fout! Vergeet niet dat de radius de helft is van de diameter.
Verkeerde eenheden gebruiken: Zorg ervoor dat alle metingen in dezelfde eenheden zijn.
Pi (π) vergeten: Vergeet niet om π (3.14159...) te gebruiken in de formule.
Het kwadraat van de radius vergeten: Je moet de radius vermenigvuldigen met zichzelf (r²).

Conclusie: Bereken met Vertrouwen!

De inhoud van een cilinder berekenen is een vaardigheid die je in veel situaties van pas kan komen. Met de formule V = π * r² * h en de tips in deze gids, kun je nu met vertrouwen de inhoud van elke cilinder berekenen. Of het nu gaat om het kiezen van de juiste bakvorm of het inschatten van de capaciteit van een watertank, je hebt nu de tools om het zelf te doen! Dus, ga erop uit en meet, bereken, en ontdek de wereld van cilinders!

Onthoud: oefening baart kunst. Probeer verschillende voorbeelden en experimenteer met verschillende cilinders om je vaardigheden te verbeteren. Voor je het weet, ben je een expert in het berekenen van de inhoud van cilinders!