Hoe Bereken Je De Oppervlakte Van Een Parallellogram

Laten we eerlijk zijn, wiskunde kan soms aanvoelen als een ondoordringbare jungle. Specifiek, het berekenen van oppervlaktes van verschillende vormen. Misschien zit je vast aan een huiswerkopdracht, of probeer je simpelweg te begrijpen hoeveel verf je nodig hebt voor een muur die toevallig de vorm heeft van een parallellogram. Wat de reden ook is, je bent niet de enige. Veel mensen worstelen met geometrie, en het is oké om hulp te zoeken.

In dit artikel duiken we diep in de wereld van parallellogrammen en hun oppervlaktes. We ontrafelen de formule, geven praktische voorbeelden, en adresseren mogelijke verwarringen. Geen ingewikkelde jargon, geen onnodige complicaties. Gewoon heldere, begrijpelijke uitleg. Het doel is simpel: je in staat stellen om de oppervlakte van een parallellogram zelfverzekerd te berekenen.

Waarom is dit belangrijk? De praktische kant van parallellogrammen

Misschien denk je: "Wanneer ga ik dit in het echte leven gebruiken?". Het antwoord: vaker dan je denkt! Parallellogrammen duiken overal op, van architectuur tot design, en zelfs in alledaagse objecten:

Architectuur en constructie: Denk aan ramen, muren (vooral bij schuine daken), en structurele componenten.
Design: Stoffen, patronen, logo's, en zelfs meubels bevatten vaak parallellogrammen of vormen die daarvan afgeleid zijn.
Kaarten en navigatie: Bij het projecteren van een bolvormige aarde op een plat vlak ontstaan vaak vervormingen, waarbij parallellogrammen een rol kunnen spelen.
Landmeetkunde: Het bepalen van de oppervlakte van stukken land met onregelmatige vormen kan efficiënter door deze op te delen in parallellogrammen en andere eenvoudige figuren.

Stel je voor dat je een nieuw terras wilt aanleggen en stenen wilt gebruiken die de vorm hebben van een parallellogram. Het correct berekenen van de oppervlakte is cruciaal om te weten hoeveel stenen je moet bestellen, voorkomend dat je te veel of te weinig koopt. Of, als je een schilder bent en een muur in de vorm van een parallellogram moet schilderen, moet je de oppervlakte kennen om te bepalen hoeveel verf je nodig hebt. De vaardigheid om de oppervlakte van een parallellogram te berekenen is dus meer dan alleen een wiskundeles; het is een praktische vaardigheid die je in verschillende situaties van pas kan komen.

De basis: Wat is een parallellogram?

Voordat we in de berekeningen duiken, is het belangrijk om te begrijpen wat een parallellogram precies is. Een parallellogram is een vierhoek (een figuur met vier zijden) waarbij de overstaande zijden evenwijdig zijn en even lang. Dit betekent dat ze nooit elkaar zullen snijden, ongeacht hoe ver je ze doortrekt.

Denk aan een rechthoek. Een rechthoek is een speciaal geval van een parallellogram, waarbij alle hoeken recht zijn (90 graden). Een vierkant is weer een speciaal geval van een rechthoek (en dus ook een parallellogram), waarbij alle zijden even lang zijn.

Belangrijke eigenschappen van een parallellogram:

Overstaande zijden zijn evenwijdig en even lang.
Overstaande hoeken zijn gelijk.
De diagonalen snijden elkaar middendoor.

De Formule: Hoe bereken je de oppervlakte?

De formule voor de oppervlakte van een parallellogram is verrassend simpel:

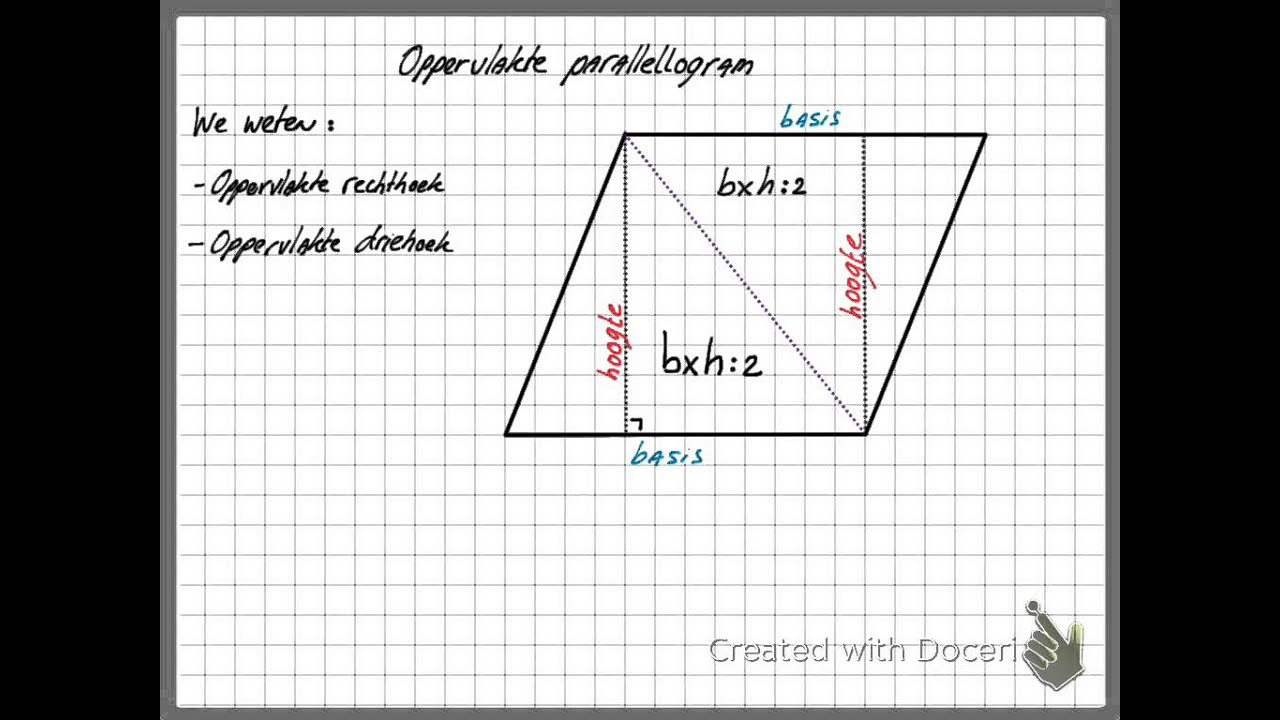
Oppervlakte = Basis x Hoogte

Laten we dit ontleden:

Basis (b): Dit is de lengte van één van de zijden van het parallellogram. Je kunt elke zijde kiezen als basis.
Hoogte (h): Dit is de loodrechte afstand van de basis tot de overstaande zijde. Belangrijk: de hoogte is *niet* de lengte van de schuine zijde! Het is de kortste afstand tussen de basis en de overstaande zijde. Stel je voor dat je een rechte lijn tekent van de bovenste zijde *loodrecht* (in een rechte hoek) naar de basis. De lengte van deze lijn is de hoogte.

Denk aan een parallellogram als een "scheefgetrokken rechthoek". Als je een driehoekig stuk van de ene kant "afknipt" en aan de andere kant "plakt", krijg je een rechthoek met dezelfde basis en hoogte als het parallellogram. Daarom is de formule hetzelfde als voor een rechthoek!

Een voorbeeld:

Stel, je hebt een parallellogram met een basis van 8 cm en een hoogte van 5 cm. De oppervlakte bereken je dan als volgt:

Oppervlakte = 8 cm x 5 cm = 40 cm²

Dus, de oppervlakte van het parallellogram is 40 vierkante centimeter.

Valkuilen en Verwarringen

De meest voorkomende fout bij het berekenen van de oppervlakte van een parallellogram is het verwarren van de hoogte met de lengte van de schuine zijde. Onthoud: de hoogte moet *loodrecht* op de basis staan. De schuine zijde is alleen relevant als je bijvoorbeeld de omtrek van het parallellogram wilt berekenen (wat weer iets anders is!).

Een andere verwarring kan ontstaan als het parallellogram "op zijn punt" staat. Het is belangrijk om de basis en de *bijbehorende* hoogte te identificeren. Je kunt het parallellogram draaien in je hoofd (of op papier) zodat het "rechtop" staat en de basis duidelijk zichtbaar is.

Alternatieve methoden (voor gevorderden)

Hoewel de formule "Basis x Hoogte" de meest gebruikelijke en eenvoudigste methode is, zijn er alternatieve methoden om de oppervlakte van een parallellogram te berekenen, afhankelijk van welke informatie je hebt:

Met behulp van trigonometrie: Als je de lengte van twee aangrenzende zijden (a en b) en de hoek (θ) tussen die zijden kent, kun je de oppervlakte berekenen met de formule: Oppervlakte = a * b * sin(θ). Dit is handig als je de hoogte niet direct weet, maar wel de hoek.
Met behulp van vectoren: Als je de vectoren die twee aangrenzende zijden van het parallellogram vertegenwoordigen kent, kun je het kruisproduct van de vectoren berekenen. De absolute waarde van de resultante vector is de oppervlakte van het parallellogram.
Door opdeling in andere vormen: Zoals eerder gezegd, kun je een parallellogram opdelen in een rechthoek en twee (congruente) driehoeken. Bereken de oppervlakte van de rechthoek en de twee driehoeken afzonderlijk, en tel ze bij elkaar op.

Deze methoden zijn minder gebruikelijk voor basisberekeningen, maar ze zijn nuttig in complexere scenario's waar de basis en hoogte niet direct gegeven zijn.

Adresseren van tegenargumenten: "Waarom zo'n ingewikkelde formule voor zo'n eenvoudige vorm?"

Sommigen beweren misschien dat de formule voor het berekenen van de oppervlakte van een parallellogram onnodig ingewikkeld is voor zo'n eenvoudige vorm. Waarom niet gewoon alle zijden vermenigvuldigen? Nou, dat zou alleen werken als het een rechthoek (of vierkant) was! Het is cruciaal om te onthouden dat de hoogte loodrecht op de basis moet staan. Het vermenigvuldigen van de schuine zijde met de basis zou een verkeerde oppervlakte opleveren.

De formule "Basis x Hoogte" is eigenlijk heel elegant, omdat het de connectie laat zien tussen parallellogrammen en rechthoeken. Het benadrukt het principe dat vormen met dezelfde basis en hoogte dezelfde oppervlakte hebben, ongeacht hun vorm.

Samenvatting en Tips

Laten we de belangrijkste punten nog eens samenvatten:

Een parallellogram is een vierhoek met overstaande zijden die evenwijdig en even lang zijn.
De oppervlakte van een parallellogram wordt berekend met de formule: Oppervlakte = Basis x Hoogte.
De hoogte is de loodrechte afstand van de basis tot de overstaande zijde.
Vermijd het verwarren van de hoogte met de lengte van de schuine zijde.
Oefen met verschillende voorbeelden om de formule te beheersen.

Extra tips:

Teken altijd een diagram van het parallellogram en label de basis en hoogte duidelijk.
Controleer je antwoord door de eenheden te controleren (oppervlakte wordt altijd uitgedrukt in vierkante eenheden).
Gebruik online calculators of geometrie software om je antwoorden te verifiëren.

Oefening baart kunst: Voorbeeldoefeningen

Om je begrip te testen, hier zijn een paar oefenvragen:

Een parallellogram heeft een basis van 12 cm en een hoogte van 7 cm. Wat is de oppervlakte?
Een parallellogram heeft een oppervlakte van 60 cm² en een basis van 10 cm. Wat is de hoogte?
Een parallellogram heeft zijden van lengte 5 cm en 8 cm, en de hoek tussen deze zijden is 60 graden. Wat is de oppervlakte? (Hint: gebruik trigonometrie)

(Antwoorden: 1. 84 cm², 2. 6 cm, 3. ≈ 34.64 cm²)

Conclusie

Het berekenen van de oppervlakte van een parallellogram is een fundamentele vaardigheid in de geometrie met praktische toepassingen in verschillende vakgebieden. Door de formule te begrijpen en veel te oefenen, kun je deze vaardigheid beheersen en zelfverzekerd parallellogrammen analyseren en berekenen.

Nu je de kennis en tools hebt om de oppervlakte van een parallellogram te berekenen, wat is het volgende geometrische probleem dat je wilt aanpakken? Of, misschien ga je de pas geleerde kennis toepassen bij je volgende doe-het-zelf project?