Hoe Bereken Je De Top Van Een Parabool

Laten we eerlijk zijn, wiskunde kan soms voelen als een doolhof. Je bent bezig met kwadratische vergelijkingen en dan komt daar plotseling de term "parabool" om de hoek kijken. En dan moet je de top ervan gaan berekenen! Geen paniek, je bent niet de enige die zich hierdoor overweldigd voelt. Veel leerlingen en zelfs professionals in bepaalde vakgebieden lopen hier tegenaan. Het goede nieuws is: het is echt niet zo ingewikkeld als het lijkt. We gaan het samen stap voor stap ontleden.

Misschien denk je: "Waarom zou ik in vredesnaam de top van een parabool willen berekenen? Heeft dat wel nut in het echte leven?" Absoluut! Parabolen komen overal voor, van de baan van een bal die je gooit tot de vorm van satelliet schotels. In de economie worden ze gebruikt om winst- en verliescurves te modelleren, in de natuurkunde om projectielbanen te berekenen, en in de engineering om bruggen en architectonische structuren te ontwerpen. De top van de parabool vertegenwoordigt in veel van deze gevallen een cruciaal punt: het maximum (zoals maximale winst of de maximale hoogte van een projectiel) of het minimum (zoals minimale kosten).

Sommigen beweren dat wiskundige concepten zoals deze te abstract zijn en geen praktische waarde hebben. "Waarom leren we dit nog op school als we toch allemaal rekenmachines hebben?" hoor je vaak. En natuurlijk, een rekenmachine kan de berekening uitvoeren. Maar begrijpen *hoe* die berekening werkt, geeft je een veel dieper inzicht in de principes die erachter zitten. Het stelt je in staat om kritisch te denken, problemen op te lossen en zelfstandig te handelen, ook als je geen rekenmachine bij de hand hebt. Bovendien helpt het je om fouten in berekeningen van anderen te herkennen.

Wat is een Parabool eigenlijk?

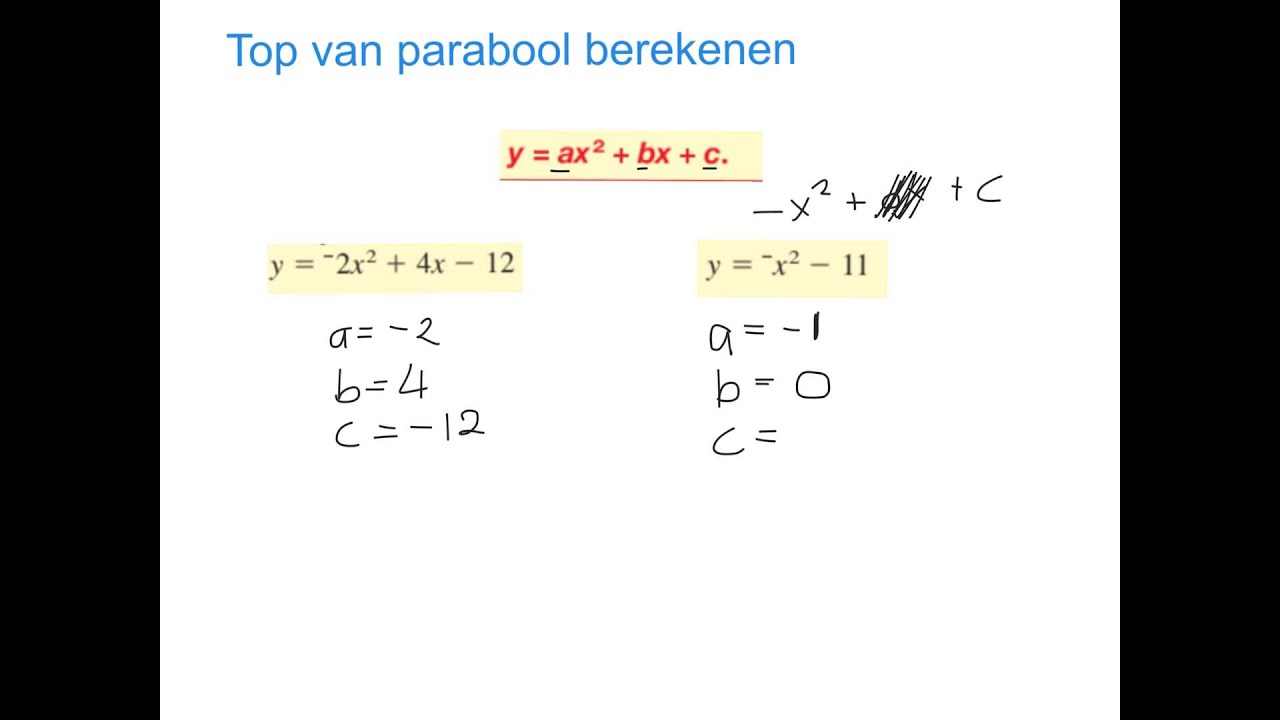
Een parabool is een U-vormige curve die wordt beschreven door een kwadratische vergelijking. De algemene vorm van zo'n vergelijking is:

y = ax² + bx + c

Waarbij a, b en c constanten zijn en a niet gelijk is aan nul. De waarde van a bepaalt of de parabool omhoog (a > 0) of omlaag (a < 0) wijst.

Stel je voor dat je een bal omhoog gooit. De baan die de bal volgt, beschrijft (bij benadering) een parabool. De top van de parabool is het punt waar de bal zijn hoogste punt bereikt voordat hij weer naar beneden valt.

De Top van de Parabool: Het Belangrijke Punt

De top van een parabool is het punt waar de parabool van richting verandert. Als de parabool omhoog wijst, is de top het laagste punt (minimum). Als de parabool omlaag wijst, is de top het hoogste punt (maximum). De top wordt weergegeven door een coördinaat (x, y).

Waarom is de Top zo belangrijk?

Optimalisatie: In veel problemen vertegenwoordigt de top de optimale oplossing (bijvoorbeeld maximale winst, minimale kosten).
Symmetrie: De top ligt op de symmetrie-as van de parabool. Dit betekent dat de parabool perfect symmetrisch is rond deze verticale lijn.
Analyse: De top geeft belangrijke informatie over het gedrag van de kwadratische functie.

Hoe Bereken je de Top? Verschillende Methoden

Er zijn verschillende manieren om de top van een parabool te berekenen. We zullen de meest gebruikelijke methoden bespreken:

1. De Formule Methode

Dit is de meest directe en snelle methode. De x-coördinaat van de top (x_top) wordt berekend met de volgende formule:

x_top = -b / 2a

Waarbij a en b de coëfficiënten zijn uit de kwadratische vergelijking y = ax² + bx + c.

Zodra je de x-coördinaat hebt, kun je de y-coördinaat van de top (y_top) berekenen door de waarde van x_top in de originele kwadratische vergelijking in te vullen:

y_top = a(x_top)² + b(x_top) + c

Voorbeeld:

Stel dat we de parabool hebben met de vergelijking y = 2x² - 8x + 6.

Hier is a = 2 en b = -8.

x_top = -(-8) / (2 * 2) = 8 / 4 = 2

y_top = 2(2)² - 8(2) + 6 = 8 - 16 + 6 = -2

Dus de top van de parabool is (2, -2).

2. Kwadraat Afsplitsen (Completing the Square)

Kwadraat afsplitsen is een iets complexere methode, maar het geeft je een dieper inzicht in de structuur van de kwadratische vergelijking. Het idee is om de vergelijking om te schrijven in de vorm:

y = a(x - h)² + k

Waarbij (h, k) de coördinaten van de top zijn.

Stappen voor kwadraat afsplitsen:

Zorg ervoor dat de coëfficiënt van x² (de waarde van a) gelijk is aan 1. Zo niet, deel dan de hele vergelijking door a.
Neem de helft van de coëfficiënt van x (de waarde van b), kwadrateer deze en tel deze waarde op en trek deze er weer af binnen de vergelijking.
Herschrijf de eerste drie termen als een volkomen kwadraat.
Vereenvoudig de vergelijking.

Voorbeeld:

Laten we dezelfde vergelijking gebruiken: y = 2x² - 8x + 6.

Deel de vergelijking door 2: y = 2(x² - 4x + 3)
Neem de helft van -4 (-2), kwadrateer het (4) en tel het op en trek het er weer af: y = 2(x² - 4x + 4 - 4 + 3)
Herschrijf als een volkomen kwadraat: y = 2((x - 2)² - 1)
Vereenvoudig: y = 2(x - 2)² - 2

Nu is de vergelijking in de vorm y = a(x - h)² + k, waarbij a = 2, h = 2 en k = -2. Dus de top is (2, -2).

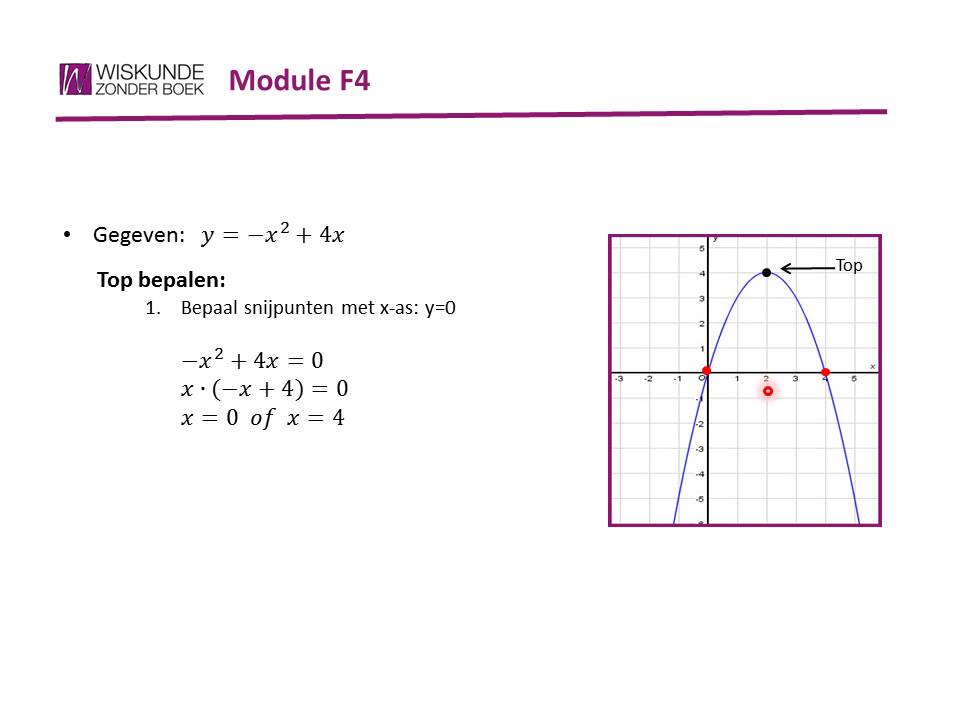
3. Grafische Methode

Als je een grafische rekenmachine of software hebt, kun je de parabool eenvoudig plotten en de top visueel bepalen. De top is het hoogste of laagste punt op de grafiek.

Voordelen:

Visueel inzicht in de parabool.
Eenvoudig te gebruiken met de juiste tools.

Nadelen:

Niet altijd nauwkeurig, vooral als de top geen gehele coördinaten heeft.
Vereist een grafische rekenmachine of software.

Veelgemaakte Fouten en Hoe ze te Vermijden

Bij het berekenen van de top van een parabool worden vaak dezelfde fouten gemaakt. Hier zijn enkele veelvoorkomende fouten en tips om ze te vermijden:

Verkeerde Formule: Zorg ervoor dat je de juiste formule gebruikt voor de x-coördinaat van de top (x_top = -b / 2a).
Tekenfouten: Let goed op de tekens van a en b in de formule. Een verkeerd teken kan leiden tot een verkeerde uitkomst.
Verkeerde Substitutie: Zorg ervoor dat je de correcte waarde van x_top in de kwadratische vergelijking invult om y_top te berekenen.
Rekenfouten: Dubbelcheck je berekeningen om slordige fouten te voorkomen.
Kwadraat Afsplitsen Moeilijkheden: Kwadraat afsplitsen kan verwarrend zijn. Oefen regelmatig om de stappen goed te begrijpen.

Praktische Toepassingen

Zoals eerder genoemd, zijn parabolen en de berekening van hun toppen van toepassing op veel gebieden. Denk aan:

Economie: Het bepalen van de maximale winst voor een bedrijf, gegeven een bepaalde kosten- en omzetfunctie.
Natuurkunde: Het berekenen van de maximale hoogte die een projectiel zal bereiken.
Engineering: Het ontwerpen van bruggen en andere structuren die paraboolvormig zijn om de krachten optimaal te verdelen.
Sport: Het analyseren van de baan van een bal die wordt gegooid of geschoten om de beste hoek en snelheid te bepalen.
Optimalisatieproblemen: Het vinden van de optimale waarde voor een bepaalde variabele in een model, zoals de optimale dosering van een medicijn.

Het begrijpen van parabolen en hun toppen is dus niet alleen relevant voor wiskunde examens, maar ook voor een breed scala aan praktische toepassingen in het dagelijks leven en in verschillende professionele vakgebieden.

Conclusie

Het berekenen van de top van een parabool is een essentieel concept in de wiskunde met tal van praktische toepassingen. Door de formules te begrijpen en de methoden te oefenen, kun je deze vaardigheid beheersen en toepassen op verschillende problemen. Of je nu de formulemethode, kwadraat afsplitsen of de grafische methode gebruikt, het belangrijkste is dat je het concept begrijpt en de stappen zorgvuldig volgt.

Welke van de beschreven methoden vind jij het meest intuïtief en welke ga je als eerste proberen toe te passen op een probleem dat je tegenkomt?