Hoeveel Diagonalen Heeft Een Tienhoek

Een tienhoek, ook wel decagoon genoemd, is een veelhoek met tien zijden en tien hoeken. Maar wist je dat een tienhoek ook een flink aantal diagonalen heeft? In dit artikel duiken we dieper in de wiskunde van de tienhoek en leggen we uit hoe je het aantal diagonalen kunt berekenen. We zullen de theorie helder uitleggen, zonder te veel te vereenvoudigen, en kijken naar de praktische toepassing van dit concept.

Wat is een Diagonaal?

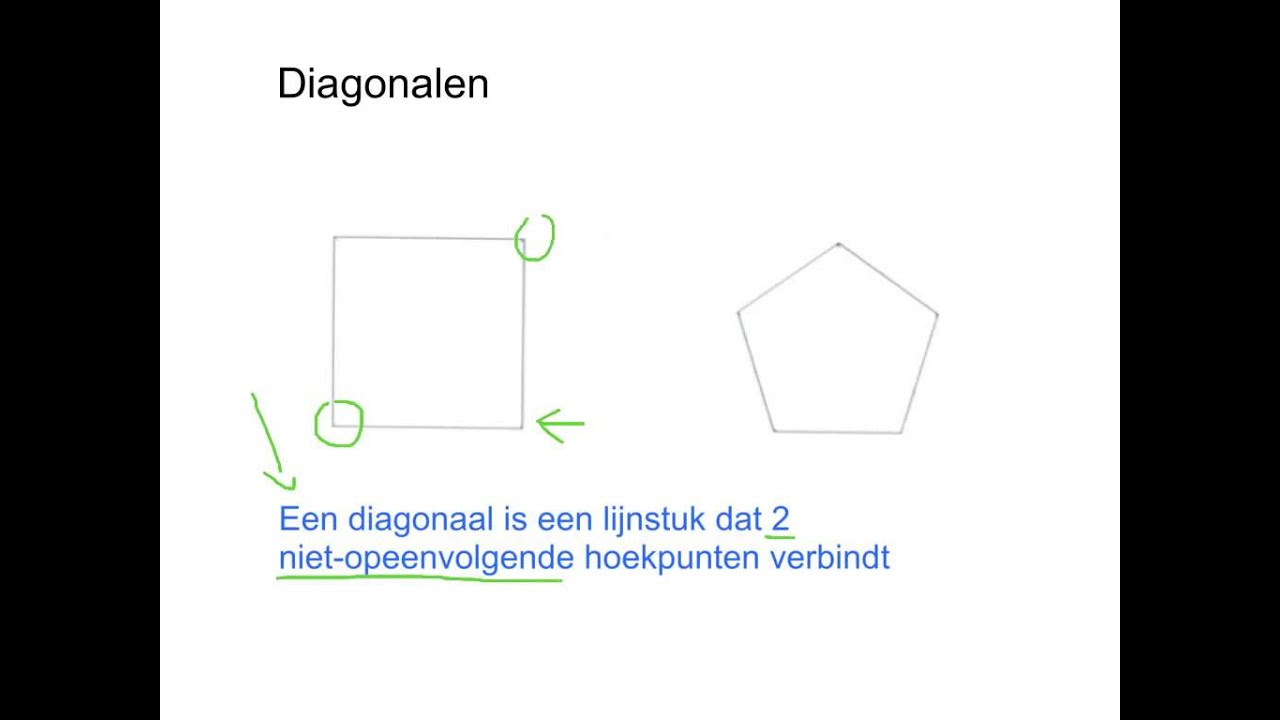
Voordat we het over de tienhoek hebben, is het belangrijk om te definiëren wat een diagonaal precies is. Een diagonaal is een lijnsegment dat twee niet-opeenvolgende hoekpunten van een veelhoek verbindt. Met andere woorden, het is een lijn die je kunt trekken binnen de veelhoek, van hoekpunt naar hoekpunt, maar niet langs een van de zijden van de veelhoek zelf.

Denk bijvoorbeeld aan een vierkant. Deze heeft twee diagonalen. Elk hoekpunt is verbonden met alle andere hoekpunten, maar we negeren de lijnen die al een zijde van het vierkant vormen. De lijnen die overblijven en binnen het vierkant lopen, zijn de diagonalen.

De Formule voor het Aantal Diagonalen

Er is een algemene formule om het aantal diagonalen in een veelhoek met *n* zijden te berekenen. Deze formule is:

D = n(n - 3) / 2

Waarbij D staat voor het aantal diagonalen en n voor het aantal zijden van de veelhoek. Deze formule is gebaseerd op het idee dat je vanuit elk hoekpunt lijnen kunt trekken naar alle andere hoekpunten, behalve naar zichzelf en de twee hoekpunten ernaast (omdat die de zijden vormen). Vervolgens deel je het resultaat door twee, omdat elke diagonaal anders geteld zou worden (van A naar B is hetzelfde als van B naar A).

Waarom n - 3?

Laten we deze component in de formule beter bekijken. De term n - 3 vertegenwoordigt het aantal hoekpunten waarmee een gegeven hoekpunt verbonden kan worden om een diagonaal te vormen. Zoals eerder gezegd, kunnen we niet verbinding maken met het hoekpunt zelf, noch met de twee aangrenzende hoekpunten (deze verbindingen vormen de zijden van de veelhoek). Dus, we trekken 3 af van het totale aantal hoekpunten (n).

Waarom delen door 2?

Het delen door 2 is essentieel om te voorkomen dat we elke diagonaal dubbel tellen. Stel dat we hoekpunt A nemen en een diagonaal tekenen naar hoekpunt C. Als we vervolgens hoekpunt C nemen, zouden we dezelfde diagonaal ook tekenen naar hoekpunt A. Om deze dubbele telling te corrigeren, delen we het totale aantal mogelijke verbindingen door 2.

Het Aantal Diagonalen van een Tienhoek Berekenen

Nu we de formule begrijpen, kunnen we deze toepassen op een tienhoek. Een tienhoek heeft 10 zijden, dus *n = 10*. We vullen dit in de formule in:

D = 10(10 - 3) / 2

D = 10(7) / 2

D = 70 / 2

D = 35

Dus, een tienhoek heeft 35 diagonalen.

Visuele Weergave: Een Tienhoek met Diagonalen

Hoewel we het aantal diagonalen wiskundig hebben berekend, kan het lastig zijn om je voor te stellen hoe die 35 diagonalen eruitzien in een tienhoek. Stel je een tienhoek voor, met tien hoekpunten. Vanuit elk hoekpunt kun je zeven diagonalen tekenen. Als je dit zorgvuldig doet, zul je zien dat er een complex netwerk van lijnen ontstaat binnen de tienhoek. Het is een visueel bewijs van de wiskundige formule die we hebben gebruikt.

Praktische Toepassingen

Hoewel het berekenen van het aantal diagonalen van een tienhoek misschien een abstract wiskundig concept lijkt, zijn er wel degelijk praktische toepassingen, vooral in de architectuur en engineering.

Architectuur

Bij het ontwerpen van gebouwen, met name koepels of structuren met veelhoekige grondplannen, is het belangrijk om de structurele stabiliteit te waarborgen. Het kennen van het aantal diagonalen, en hun posities, kan helpen bij het berekenen van de krachten en spanningen binnen de structuur. Ingenieurs kunnen deze informatie gebruiken om de beste plaatsing van steunpilaren en verstevigingen te bepalen, zodat het gebouw veilig en stabiel is.

Stel je voor dat je een koepel ontwerpt met een tienhoekige basis. Het bepalen van de optimale plaatsing van steunbalken die de diagonale verbindingen volgen, kan de algehele sterkte van de koepel aanzienlijk verbeteren. Deze balken verdelen de belasting gelijkmatiger en voorkomen dat de structuur bezwijkt onder druk.

Engineering

In de engineering, en met name de civiele techniek, is het begrijpen van geometrische eigenschappen essentieel voor het ontwerpen van bruggen, tunnels en andere structuren. Het aantal diagonalen in een veelhoekige constructie kan invloed hebben op de manier waarop de structuur belastingen verdeelt en weerstaat.

Bijvoorbeeld, bij het ontwerpen van een brug met een complex traliewerk, kan het optimaliseren van het aantal diagonalen in de tralies de sterkte-gewichtsverhouding van de brug verbeteren. Een goed ontworpen traliewerk verdeelt de belasting gelijkmatig over alle onderdelen, waardoor de brug lichter en efficiënter wordt.

Computer Graphics en Game Development

Zelfs in de wereld van computer graphics en game development speelt de kennis van veelhoeken en hun eigenschappen een rol. Bij het modelleren van 3D-objecten worden vaak veelhoeken gebruikt om de vormen te definiëren. Het begrijpen van de relaties tussen hoekpunten en diagonalen kan helpen bij het optimaliseren van de modellen en het verbeteren van de prestaties van de graphics engine.

Bijvoorbeeld, als een game-ontwerper een tienhoekige toren wil modelleren, kan hij de formule voor het aantal diagonalen gebruiken om het aantal vertices en faces te minimaliseren, zonder de visuele kwaliteit van de toren aan te tasten. Dit resulteert in een efficiënter model dat minder resources verbruikt en de game sneller laat draaien.

Conclusie

Het aantal diagonalen van een tienhoek, 35, is meer dan alleen een wiskundig feit. Het vertegenwoordigt een fundamenteel aspect van de geometrie van veelhoeken, met toepassingen in diverse velden zoals architectuur, engineering en computer graphics. Door de formule voor het aantal diagonalen te begrijpen en toe te passen, kunnen we inzicht krijgen in de structurele eigenschappen van objecten en optimalisaties doorvoeren die leiden tot efficiëntere en stabielere ontwerpen.

Daag jezelf uit: onderzoek het aantal diagonalen van andere veelhoeken, zoals een zeshoek of een twaalfhoek. Probeer te bedenken in welke andere situaties de kennis van diagonalen van pas kan komen. Door te blijven leren en experimenteren, zul je je wiskundig begrip verdiepen en nieuwe toepassingen ontdekken.