Hoeveel Graden Is Een Parallellogram

Heb je ooit naar een ruit gekeken en je afgevraagd hoe alle hoeken precies samenhangen? Of misschien zit je vast aan een huiswerkopdracht over meetkunde en is de hoek van een parallellogram de struikelblok? Geen zorgen, je bent niet de enige. Meetkunde kan soms voelen als een doolhof van regels en definities. Maar met de juiste uitleg, wordt het opeens een stuk begrijpelijker. Laten we samen de wondere wereld van parallellogrammen induiken en ontdekken hoeveel graden ze hebben!

Wat is een parallellogram precies?

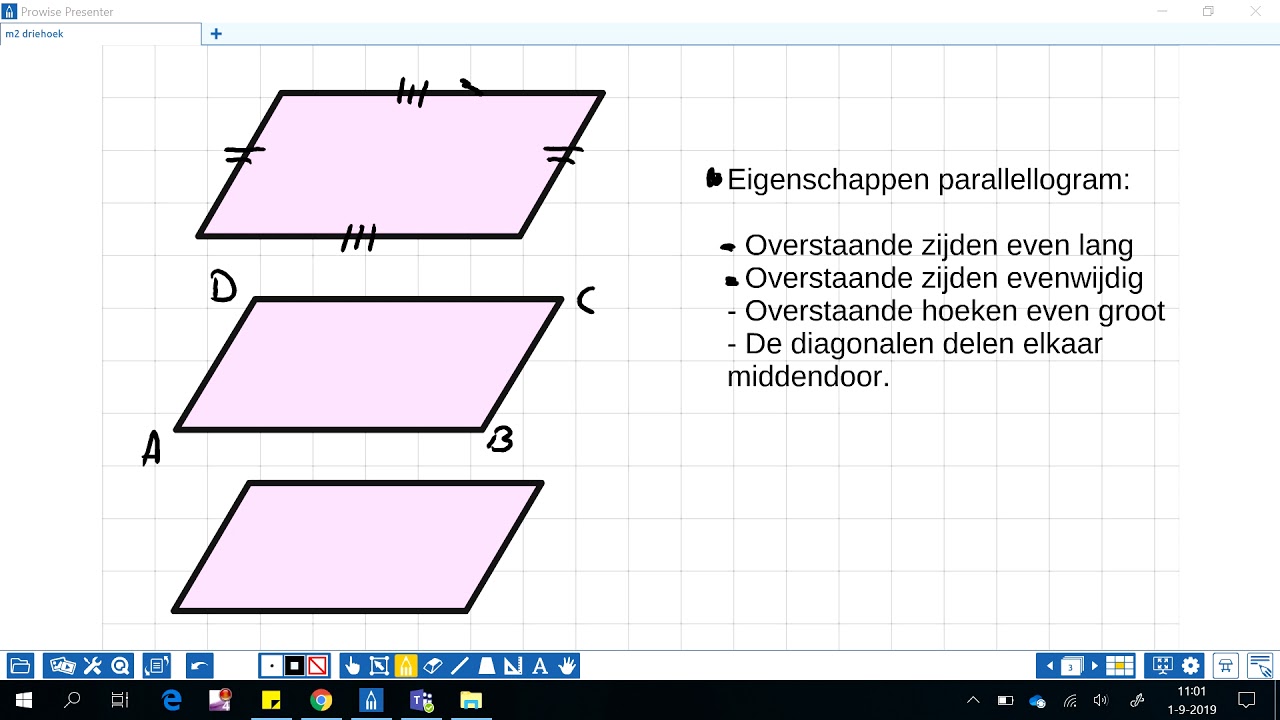
Voordat we ons verdiepen in de hoeken, is het belangrijk om een goed begrip te hebben van wat een parallellogram is. Een parallellogram is een vierhoek, wat betekent dat het een figuur is met vier zijden en vier hoeken. Het belangrijkste kenmerk van een parallellogram is dat de overstaande zijden parallel en even lang zijn. Dit is cruciaal om de eigenschappen van de hoeken te begrijpen.

Denk aan een rechthoek die een beetje is ingedrukt of uitgerekt. Dat is in feite een parallellogram! Een rechthoek en een vierkant zijn namelijk ook speciale gevallen van een parallellogram.

Belangrijke eigenschappen van een parallellogram:

• Overstaande zijden zijn parallel: Dit betekent dat de zijden elkaar nooit zullen snijden, zelfs als ze oneindig worden doorgetrokken.
• Overstaande zijden zijn even lang: De lengte van de ene zijde is gelijk aan de lengte van de zijde er recht tegenover.
• Overstaande hoeken zijn gelijk: De hoek die tegenover een andere hoek ligt, heeft dezelfde grootte.
• Aanliggende hoeken zijn supplementair: Dit betekent dat de som van twee hoeken die aan elkaar grenzen, altijd 180 graden is.
• De diagonalen snijden elkaar middendoor: De lijnen die de tegenoverliggende hoekpunten verbinden, snijden elkaar in hun middelpunt.

De som van de hoeken in een parallellogram

Net als bij elke andere vierhoek, is de som van de binnenhoeken in een parallellogram altijd 360 graden. Dit is een fundamenteel principe van meetkunde en geldt voor alle vierhoeken, ongeacht hun vorm. Dit kun je bewijzen door een vierhoek op te delen in twee driehoeken. Elke driehoek heeft een hoekensom van 180 graden, dus twee driehoeken hebben samen 360 graden.

Waarom is dit belangrijk? Omdat als je de grootte van één of twee hoeken in een parallellogram weet, je de grootte van de andere hoeken kunt berekenen. Dit is de sleutel tot het oplossen van meetkundige problemen.

Hoe bereken je de hoeken van een parallellogram?

Hier komt de magie van de eigenschappen van parallellogrammen om de hoek kijken! Zoals we al zeiden, zijn overstaande hoeken gelijk en zijn aanliggende hoeken supplementair. Laten we eens kijken naar een paar scenario's:

1. Je kent één hoek: Stel dat één hoek van een parallellogram 70 graden is. De hoek er recht tegenover is dan ook 70 graden. De aanliggende hoeken zijn supplementair, dus ze zijn 180 - 70 = 110 graden. De hoek tegenover deze hoek is dan ook 110 graden.
2. Je kent een verhouding tussen twee hoeken: Stel dat de verhouding tussen twee aanliggende hoeken 2:3 is. Dit betekent dat je de hoeken kunt representeren als 2x en 3x. Omdat ze supplementair zijn, geldt 2x + 3x = 180 graden. Dit betekent 5x = 180 graden, dus x = 36 graden. De hoeken zijn dan 2 * 36 = 72 graden en 3 * 36 = 108 graden.
3. Je hebt andere informatie, zoals de lengte van de zijden en een diagonaal: In complexere gevallen kun je trigonometrie (sinus, cosinus, tangens) of de cosinusregel nodig hebben om de hoeken te berekenen. Dit vereist meer wiskundige kennis, maar het principe blijft hetzelfde: gebruik de eigenschappen van het parallellogram en de gegeven informatie om de ontbrekende hoeken te vinden.

Voorbeeld: Stel een parallellogram ABCD, waarbij ∠A = 60 graden. Hoeveel graden is ∠C? Omdat overstaande hoeken in een parallellogram gelijk zijn, is ∠C ook 60 graden.

Voorbeeld: Stel een parallellogram PQRS, waarbij ∠P = 120 graden. Hoeveel graden is ∠Q? Omdat aanliggende hoeken supplementair zijn, is ∠Q = 180 - 120 = 60 graden.

Waarom is dit belangrijk in het echte leven?

Je denkt misschien: "Wanneer ga ik dit ooit gebruiken?" Nou, parallellogrammen en hun eigenschappen komen vaker voor dan je denkt! Architecten en ingenieurs gebruiken deze principes bij het ontwerpen van gebouwen en structuren. Denk aan bruggen, daken, en zelfs bepaalde meubelstukken. De stabiliteit en de hoekberekeningen zijn cruciaal voor de veiligheid en functionaliteit.

Ook in de kunstwereld zie je parallellogrammen terug. Kunstenaars gebruiken ze om perspectief en diepte te creëren in hun schilderijen en tekeningen. Het begrijpen van de hoeken helpt hen om realistische en evenwichtige composities te maken.

In het dagelijks leven kom je ze tegen in tegels, ruiten, en zelfs de manier waarop je spullen stapelt. Een beter begrip van meetkunde maakt je meer bewust van de vormen en structuren om je heen.

Praktische tips en trucs

• Teken een diagram: Het visueel weergeven van het probleem helpt enorm. Teken een parallellogram en label de bekende hoeken en zijden.
• Gebruik een geodriehoek: Meet hoeken nauwkeurig met een geodriehoek.
• Oefen, oefen, oefen: Hoe meer problemen je oplost, hoe beter je de concepten zult begrijpen.
• Zoek online hulp: Er zijn talloze websites en video's die meetkundige concepten uitleggen. Zoek naar tutorials en oefenopgaven.
• Vraag om hulp: Schroom niet om je leraar, een klasgenoot of een online forum om hulp te vragen als je vastzit.

Conclusie

Een parallellogram heeft, net als elke vierhoek, een totale hoekensom van 360 graden. De sleutel tot het begrijpen en berekenen van de hoeken in een parallellogram ligt in het kennen van de eigenschappen: overstaande hoeken zijn gelijk en aanliggende hoeken zijn supplementair. Met deze kennis en een beetje oefening, kun je elk parallellogram-hoekprobleem aanpakken! Dus, daag jezelf uit, pak je geodriehoek en duik in de fascinerende wereld van meetkunde. Je zult versteld staan van wat je kunt bereiken.

Onthoud: wiskunde is geen hekserij, maar een verzameling logische principes. Met de juiste aanpak kan iedereen het leren en begrijpen. Succes!

Samenvattend:

• Een parallellogram is een vierhoek met overstaande zijden die parallel en even lang zijn.
• De som van de binnenhoeken van een parallellogram is 360 graden.
• Overstaande hoeken in een parallellogram zijn gelijk.
• Aanliggende hoeken in een parallellogram zijn supplementair (som is 180 graden).