Hoeveel Graden Is Een Rechte Hoek

Heb je je ooit afgevraagd hoeveel graden er in een hoek zit? Of misschien heb je een kind dat worstelt met meetkunde en je wilt ze helpen het concept te begrijpen? Het is een veelvoorkomende vraag, en het antwoord is eenvoudiger dan je misschien denkt.

In dit artikel leggen we uit wat een rechte hoek is, hoeveel graden hij bevat en hoe je hem kunt herkennen. We maken gebruik van heldere uitleg en praktische voorbeelden om het begrijpen ervan zo gemakkelijk mogelijk te maken.

Wat is een Rechte Hoek?

Laten we beginnen met de basis. Een rechte hoek is een hoek die precies 90 graden meet. Je kunt hem herkennen aan zijn kenmerkende vorm: hij ziet eruit als een perfecte "L".

Stel je voor dat je een vierkant of een rechthoek hebt. Elke hoek van die vorm is een rechte hoek. Denk aan de hoeken van een deurkozijn, de hoek van een kruispunt, of de hoek van een vel papier. Dit zijn allemaal voorbeelden van rechte hoeken in de dagelijkse omgeving.

Waarom is 90 graden zo belangrijk? Omdat het een fundamentele referentiepunt is in de meetkunde. Het dient als basis voor het meten van andere hoeken. Hoeken kleiner dan 90 graden noemen we scherpe hoeken, en hoeken groter dan 90 graden, maar kleiner dan 180 graden, noemen we stompe hoeken.

Hoe Herken je een Rechte Hoek?

Er zijn verschillende manieren om een rechte hoek te identificeren:

• Met het blote oog: Zoals gezegd, een rechte hoek ziet er uit als een perfecte "L".
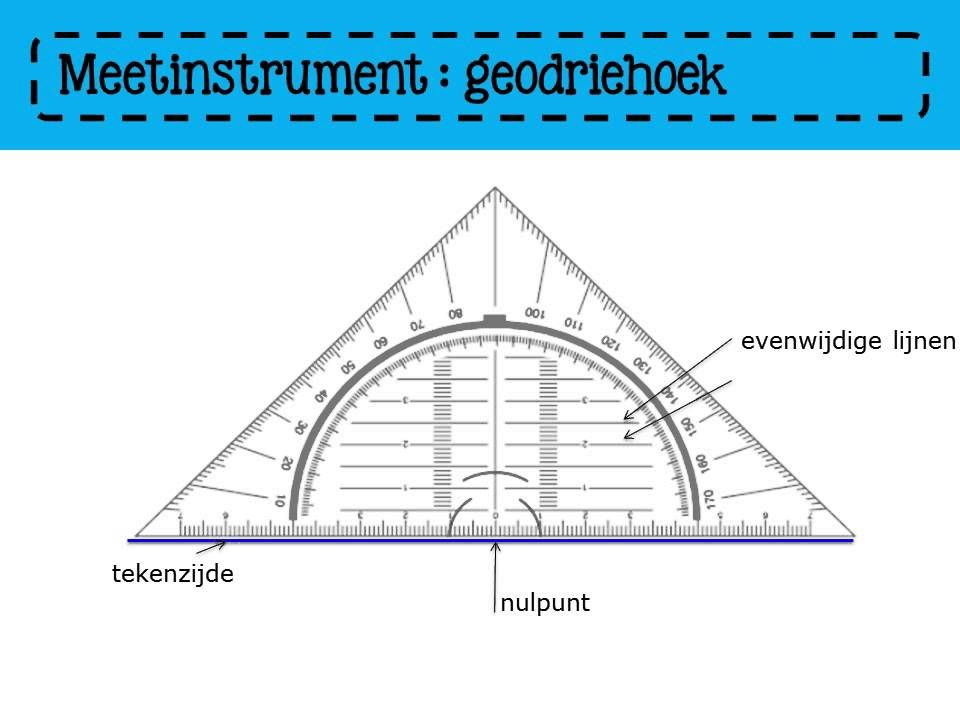
• Met een geodriehoek: Een geodriehoek heeft een specifieke markering (een klein vierkantje) in een van de hoeken om een rechte hoek aan te duiden. Leg de geodriehoek op de hoek die je wilt controleren. Als de hoek van de geodriehoek perfect overeenkomt met de hoek die je meet, dan is het een rechte hoek.
• Met een gradenboog: Een gradenboog is een instrument om hoeken te meten. Plaats de gradenboog zo dat het middelpunt op het hoekpunt van de hoek ligt en een van de lijnen van de hoek op de 0-gradenmarkering. Als de andere lijn van de hoek de 90-gradenmarkering raakt, dan is het een rechte hoek.
• Door te meten: Als je de zijden van een driehoek kent, kun je de stelling van Pythagoras gebruiken om te bepalen of het een rechthoekige driehoek is (een driehoek met een rechte hoek).

Waarom is Kennis van Rechte Hoeken Belangrijk?

Kennis van rechte hoeken is cruciaal in veel verschillende gebieden:

• Architectuur en Bouwkunde: Rechte hoeken zijn essentieel voor het ontwerpen en bouwen van gebouwen. Muren, vloeren en plafonds moeten perfecte rechte hoeken vormen om stabiliteit en structuur te garanderen.
• Engineering: Ingenieurs gebruiken rechte hoeken bij het ontwerpen van bruggen, machines en andere constructies. Nauwkeurigheid is van het grootste belang, en rechte hoeken bieden een betrouwbare referentie.
• Navigatie: Cartografie en navigatie zijn afhankelijk van nauwkeurige hoekmetingen. Rechte hoeken worden gebruikt om kaarten te maken en routes te bepalen.
• Computergraphics en Game Development: Rechte hoeken zijn belangrijk in 2D- en 3D-modellen die in computerspellen en grafische ontwerpen worden gebruikt.
• Dagelijks Leven: Van het ophangen van een schilderij tot het inrichten van een kamer, het begrijpen van rechte hoeken helpt ons om dingen recht en evenwijdig te plaatsen.

Denk bijvoorbeeld aan het ophangen van een plank. Als de plank niet recht is, zal alles wat erop staat er scheef uitzien en kan het er zelfs afvallen. Hetzelfde geldt voor het plaatsen van meubels in een kamer. Als de meubels niet evenwijdig aan de muren staan, kan de kamer er oncomfortabel en ongeorganiseerd uitzien.

Rechte Hoeken in de Meetkunde

In de meetkunde spelen rechte hoeken een belangrijke rol in verschillende concepten en stellingen.

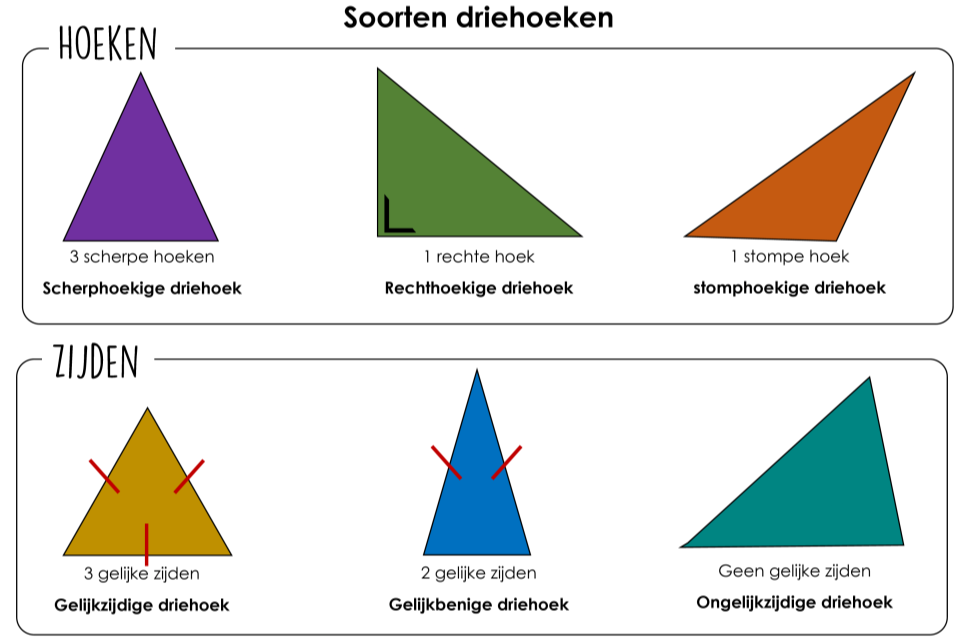
• Rechthoekige Driehoeken: Een rechthoekige driehoek is een driehoek die één rechte hoek bevat. De zijde tegenover de rechte hoek wordt de hypotenusa genoemd, en de andere twee zijden worden de rechthoekszijden genoemd. De stelling van Pythagoras, die de relatie tussen de lengtes van de zijden van een rechthoekige driehoek beschrijft, is een fundamenteel concept in de meetkunde.
• Vierkanten en Rechthoeken: Zoals eerder vermeld, hebben vierkanten en rechthoeken vier rechte hoeken. Deze eigenschap maakt ze tot belangrijke vormen in de meetkunde en in het dagelijks leven.
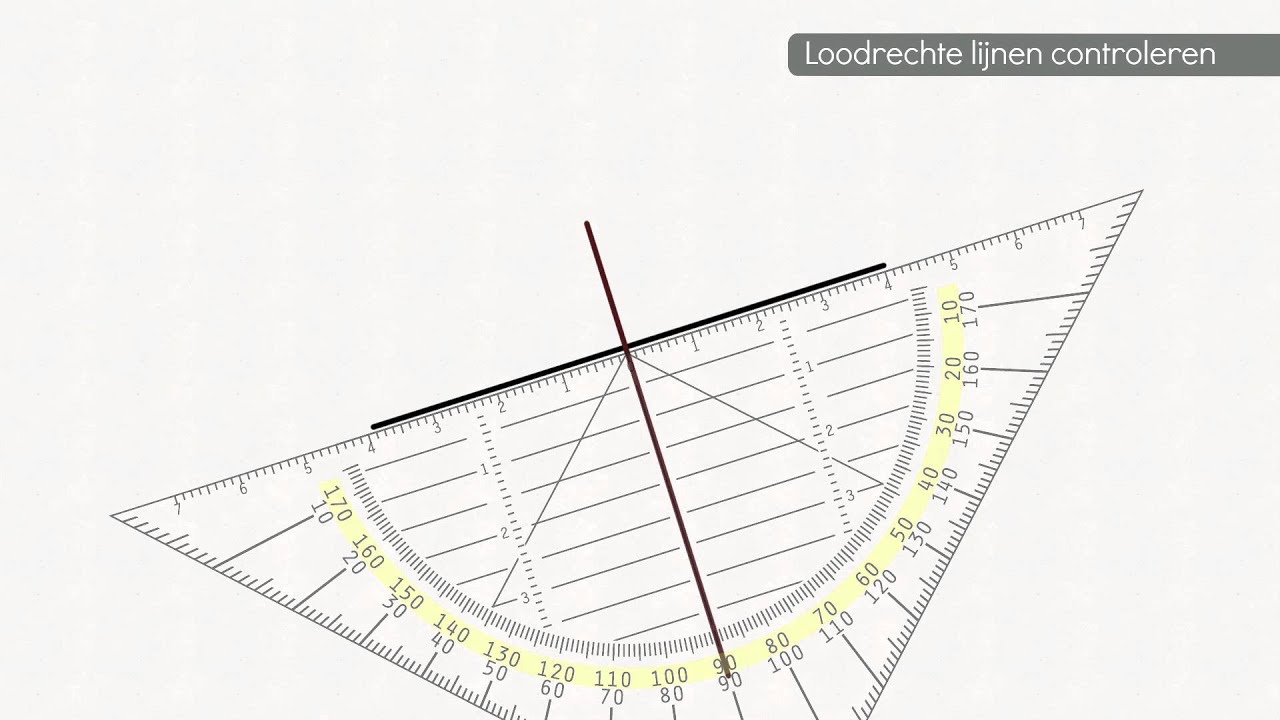
• Lijnen en Loodlijnen: Twee lijnen die elkaar snijden onder een rechte hoek worden loodlijnen genoemd. Loodlijnen zijn belangrijk in veel geometrische constructies en bewijzen.

De stelling van Pythagoras stelt dat in een rechthoekige driehoek het kwadraat van de lengte van de hypotenusa gelijk is aan de som van de kwadraten van de lengtes van de rechthoekszijden (a² + b² = c²). Deze stelling is van onschatbare waarde bij het oplossen van problemen waarbij rechthoekige driehoeken betrokken zijn.

Praktische Voorbeelden en Oefeningen

Laten we een paar praktische voorbeelden en oefeningen bekijken om je begrip van rechte hoeken te versterken.

Voorbeeld 1: Je wilt een fotolijst recht aan de muur hangen. Hoe kun je ervoor zorgen dat de lijst waterpas hangt?

Oplossing: Gebruik een waterpas. Een waterpas heeft een bubbel in een buisje met vloeistof. Wanneer de bubbel in het midden van de buis staat, is het object horizontaal of verticaal (afhankelijk van hoe je de waterpas gebruikt). Houd de waterpas tegen de bovenkant van de fotolijst en pas de lijst aan totdat de bubbel in het midden staat. Je kunt ook een geodriehoek gebruiken om te controleren of de bovenkant van de lijst een rechte hoek maakt met de muur.

Voorbeeld 2: Je wilt een rechthoekige tafel maken. Hoe zorg je ervoor dat de hoeken van de tafel recht zijn?

Oplossing: Gebruik een geodriehoek of een gradenboog om de hoeken te meten terwijl je de tafel in elkaar zet. Je kunt ook de "3-4-5" regel gebruiken. Meet 3 eenheden (bijvoorbeeld centimeters) langs de ene zijde van de hoek en 4 eenheden langs de andere zijde. Als de afstand tussen de eindpunten van deze twee metingen 5 eenheden is, dan is de hoek recht. Dit is een directe toepassing van de stelling van Pythagoras (3² + 4² = 5²).

Oefening: Kijk eens rond in je huis of klaslokaal. Probeer zoveel mogelijk voorbeelden van rechte hoeken te vinden. Kun je rechte hoeken vinden in ramen, deuren, boeken, of andere objecten?

Conclusie

Een rechte hoek is 90 graden. Het is een fundamenteel concept in de meetkunde en is van belang in veel verschillende gebieden, van architectuur en engineering tot navigatie en het dagelijks leven. Door te begrijpen wat een rechte hoek is en hoe je hem kunt herkennen, kun je problemen oplossen, objecten recht plaatsen, en een beter begrip krijgen van de wereld om je heen.

We hopen dat dit artikel je heeft geholpen om het concept van een rechte hoek beter te begrijpen. Blijf oefenen en je zult al snel een expert zijn in het herkennen en gebruiken van rechte hoeken in je dagelijkse leven!

Onthoud: oefening baart kunst! Dus, pak een geodriehoek, een gradenboog of gewoon je ogen en begin met het verkennen van de wereld van rechte hoeken!