Hoeveel Graden Is Een Vlieger

De vraag "Hoeveel graden is een vlieger?" is op het eerste gezicht misschien wat verwarrend. Het gaat hier niet om de temperatuur van een vlieger, maar om de hoeken binnen de geometrische figuur die we een vlieger noemen. In dit artikel duiken we diep in de wiskunde achter de vlieger, bekijken we de eigenschappen van zijn hoeken, en illustreren we dit met voorbeelden.

De Geometrie van een Vlieger

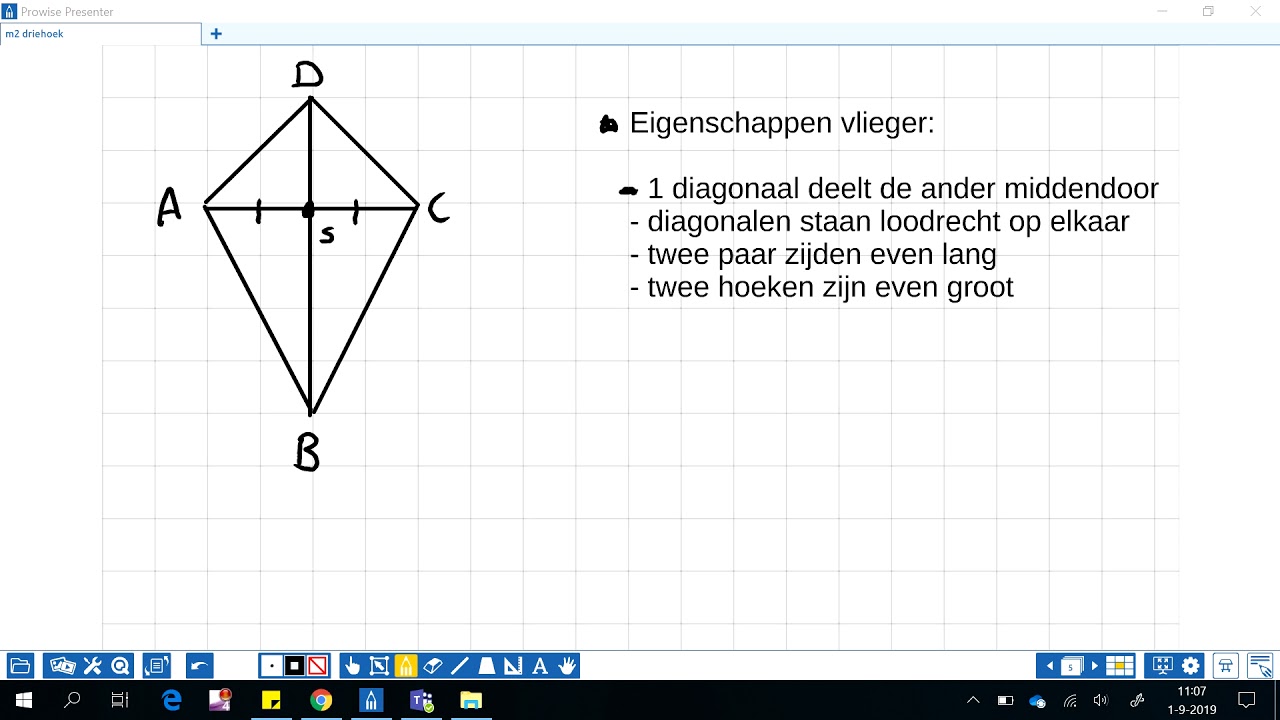
Een vlieger, ook wel deltoïde genoemd, is een vierhoek met twee paar aanliggende zijden die gelijk zijn. Dit betekent dat er twee sets van twee zijden zijn die aan elkaar grenzen en even lang zijn. Dit is een cruciaal verschil met bijvoorbeeld een parallellogram, waar de overstaande zijden gelijk zijn.

Belangrijkste Eigenschappen

Om de hoeken van een vlieger te begrijpen, is het essentieel om de belangrijkste eigenschappen ervan te kennen:

• Twee paar gelijke, aanliggende zijden: Zoals eerder genoemd, dit is de basisdefinitie.
• Eén paar gelijke hoeken: De hoeken die *tussen* de ongelijke zijden liggen, zijn gelijk aan elkaar.
• Één symmetrie-as: De diagonaal die de hoeken *tussen* de gelijke zijden deelt, is de symmetrie-as van de vlieger.
• Diagonale eigenschappen: De diagonalen staan loodrecht op elkaar. Eén diagonaal deelt de andere diagonaal in twee gelijke delen.

Deze eigenschappen zijn essentieel om de hoeken te berekenen of te bepalen.

De Hoeken van een Vlieger

Een vierhoek heeft altijd een totale hoekensom van 360 graden. Dit geldt dus ook voor een vlieger. De crux zit hem in de verdeling van die 360 graden over de vier hoeken.

Het Gelijke Hoeken Paar

Zoals hierboven vermeld, heeft een vlieger één paar gelijke hoeken. Laten we deze hoeken α (alpha) noemen. Deze hoeken bevinden zich tussen de *ongelijke* zijden van de vlieger. Dit is een belangrijk onderscheid, want de andere twee hoeken zijn in het algemeen niet gelijk aan elkaar.

De Overige Twee Hoeken

Laten we de twee overige hoeken β (beta) en γ (gamma) noemen. Deze hoeken liggen tussen de *gelijke* zijden. Deze hoeken zijn niet noodzakelijk gelijk aan elkaar. De enige uitzondering hierop is wanneer de vlieger een ruit is. Een ruit is een speciaal geval van een vlieger waarbij alle zijden gelijk zijn. In dat geval zijn alle hoeken 90 graden, of de overstaande hoeken gelijk (zoals bij elke ruit).

De Som van de Hoeken

Omdat de som van de hoeken in een vierhoek 360 graden is, geldt de volgende formule voor een vlieger:

α + α + β + γ = 360°

2α + β + γ = 360°

Dit betekent dat als je de waarde van één van de hoeken α, β, of γ weet, samen met de waarde van een *andere* hoek, je de resterende hoek kan berekenen.

Voorbeelden en Berekeningen

Laten we een paar voorbeelden bekijken om dit duidelijker te maken:

Voorbeeld 1: Bekende Hoek α

Stel dat hoek α = 70 graden, en hoek β = 110 graden. Wat zijn de waarden van hoek γ?

We gebruiken de formule: 2α + β + γ = 360°

2(70°) + 110° + γ = 360°

140° + 110° + γ = 360°

250° + γ = 360°

γ = 360° - 250°

γ = 110°

In dit geval is hoek γ dus 110 graden.

Voorbeeld 2: Een Ruit als Speciale Vlieger

Stel dat we een ruit hebben. Een ruit is een speciale vlieger waarbij alle zijden gelijk zijn. Laten we aannemen dat één van de hoeken (β) 60 graden is. Wat zijn de andere hoeken?

In een ruit zijn de overstaande hoeken gelijk. Dus γ = β = 60 graden.

Nu gebruiken we de formule: 2α + β + γ = 360°

2α + 60° + 60° = 360°

2α + 120° = 360°

2α = 240°

α = 120°

Dus de overstaande hoeken zijn 120 graden. In een ruit zijn er twee hoeken van 60 graden en twee hoeken van 120 graden.

Real-World Voorbeelden en Toepassingen

Hoewel je misschien niet dagelijks hoeken van vliegers berekent, is het concept wel relevant in diverse velden:

• Architectuur: Bij het ontwerpen van daken of gevels kunnen vliegervormige elementen voorkomen, waarbij het van belang is om de hoeken nauwkeurig te bepalen voor de structurele integriteit en esthetiek.
• Luchtvaart: De vleugels van sommige vliegtuigen hebben een vorm die lijkt op een vlieger. De hoek van de vleugel (de pijlstelling) is cruciaal voor de aerodynamica.
• Grafisch Ontwerp: Vliegers worden vaak gebruikt in logo's en ontwerpen. Het begrijpen van de hoeken helpt bij het creëren van visueel aantrekkelijke en evenwichtige composities.
• Game Development: Vliegervormen worden gebruikt om objecten te modelleren in computerspellen. De hoeken zijn essentieel voor de correcte rendering en physics simulaties.

Conclusie

De vraag "Hoeveel graden is een vlieger?" heeft dus geen eenduidig antwoord. De hoeken van een vlieger variëren, maar ze voldoen altijd aan de formule 2α + β + γ = 360°. Het belangrijkste is het begrijpen van de eigenschappen van een vlieger en hoe deze de hoeken beïnvloeden.

Door de basisprincipes van de geometrie te begrijpen, kun je de hoeken van een vlieger berekenen en toepassen in verschillende situaties. Of het nu gaat om het ontwerpen van een dak, het analyseren van een logo, of simpelweg het oplossen van een meetkundige puzzel, de kennis van de hoeken van een vlieger kan van pas komen. Dus, duik in de wiskunde, experimenteer met verschillende waarden, en ontdek de fascinerende wereld van de vlieger!