Hoeveel Graden Zijn De Hoeken Van Een Driehoek Samen

Heb je je ooit afgevraagd wat de magische formule is die de hoeken van een driehoek bij elkaar houdt? Het is een fundamenteel concept in de meetkunde dat je niet alleen helpt bij wiskundeproblemen, maar ook een beter begrip geeft van de wereld om je heen. Misschien zit je vast aan een huiswerkopdracht, of probeer je simpelweg beter te begrijpen hoe vormen werken. Wat je reden ook is, je bent hier op de juiste plek.

Het is een veelvoorkomend probleem: je staart naar een driehoek en je wordt geconfronteerd met de vraag: "Hoeveel graden zijn de hoeken van deze figuur samen?" Het antwoord is verrassend eenvoudig en fundamenteel voor het begrijpen van geometrie: de hoeken van elke driehoek, ongeacht de vorm of grootte, zijn altijd samen 180 graden. Dit is een van de meest essentiële concepten in de wiskunde en heeft toepassingen in verschillende vakgebieden, van architectuur tot navigatie.

Laten we duiken in de details en dit belangrijke concept verder onderzoeken. We gaan kijken naar waarom dit zo is, hoe je dit kunt gebruiken om problemen op te lossen, en enkele interessante toepassingen in de echte wereld.

Waarom is de som van de hoeken van een driehoek altijd 180 graden?

Om dit te begrijpen, moeten we kijken naar een paar basisprincipes van de geometrie. Stel je een rechte lijn voor. Een rechte lijn heeft een hoek van 180 graden. Nu, stel je voor dat je een driehoek tekent en deze "platdrukt" tot een rechte lijn. Dit kan je helpen visualiseren waarom de hoeken van een driehoek optellen tot 180 graden.

Er is ook een meer formele bewijs dat we kunnen overwegen:

Teken een driehoek.
Teken een lijn parallel aan een van de zijden van de driehoek door de tegenoverliggende hoekpunt.
Gebruik de eigenschappen van wisselende binnenhoeken om aan te tonen dat de hoeken langs de parallelle lijn gelijk zijn aan de hoeken van de driehoek.
Omdat de hoeken langs de parallelle lijn samen 180 graden vormen, zijn de hoeken van de driehoek ook 180 graden.

Dit bewijs laat zien dat het geen toeval is. Het is een fundamentele eigenschap van de Euclidische geometrie. Of de driehoek nu groot of klein is, gelijkzijdig, gelijkbenig of ongelijkzijdig, de som van de hoeken blijft constant.

Verschillende soorten driehoeken en de som van hun hoeken

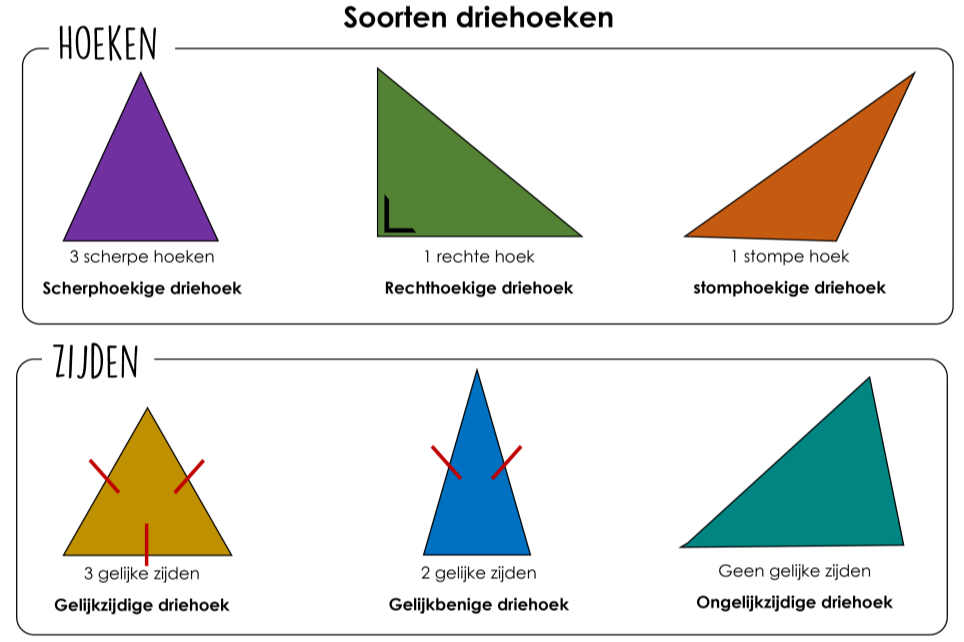
Het is belangrijk om te onthouden dat de regel van 180 graden geldt voor *alle* driehoeken, ongeacht hun type. Laten we een paar soorten driehoeken bekijken:

Gelijkzijdige driehoek: Alle zijden en hoeken zijn gelijk (60 graden per hoek). 60 + 60 + 60 = 180 graden.
Gelijkbenige driehoek: Twee zijden en twee hoeken zijn gelijk. De derde hoek kan verschillen, maar de som blijft 180 graden.
Ongelijkzijdige driehoek: Alle zijden en hoeken zijn verschillend, maar de som van de hoeken is nog steeds 180 graden.
Rechthoekige driehoek: Eén hoek is 90 graden (een rechte hoek). De som van de andere twee hoeken is dus 90 graden (omdat 90 + 90 = 180).
Scherphoekige driehoek: Alle hoeken zijn kleiner dan 90 graden.
Stomphoekige driehoek: Eén hoek is groter dan 90 graden.

Zoals je ziet, ongeacht de specifieke kenmerken van de driehoek, blijft de som van de hoeken altijd 180 graden. Dit is een krachtig en universeel principe.

Hoe gebruik je deze kennis om problemen op te lossen?

De wetenschap dat de hoeken van een driehoek 180 graden zijn, is ongelooflijk nuttig bij het oplossen van geometrische problemen. Hier zijn een paar praktische voorbeelden:

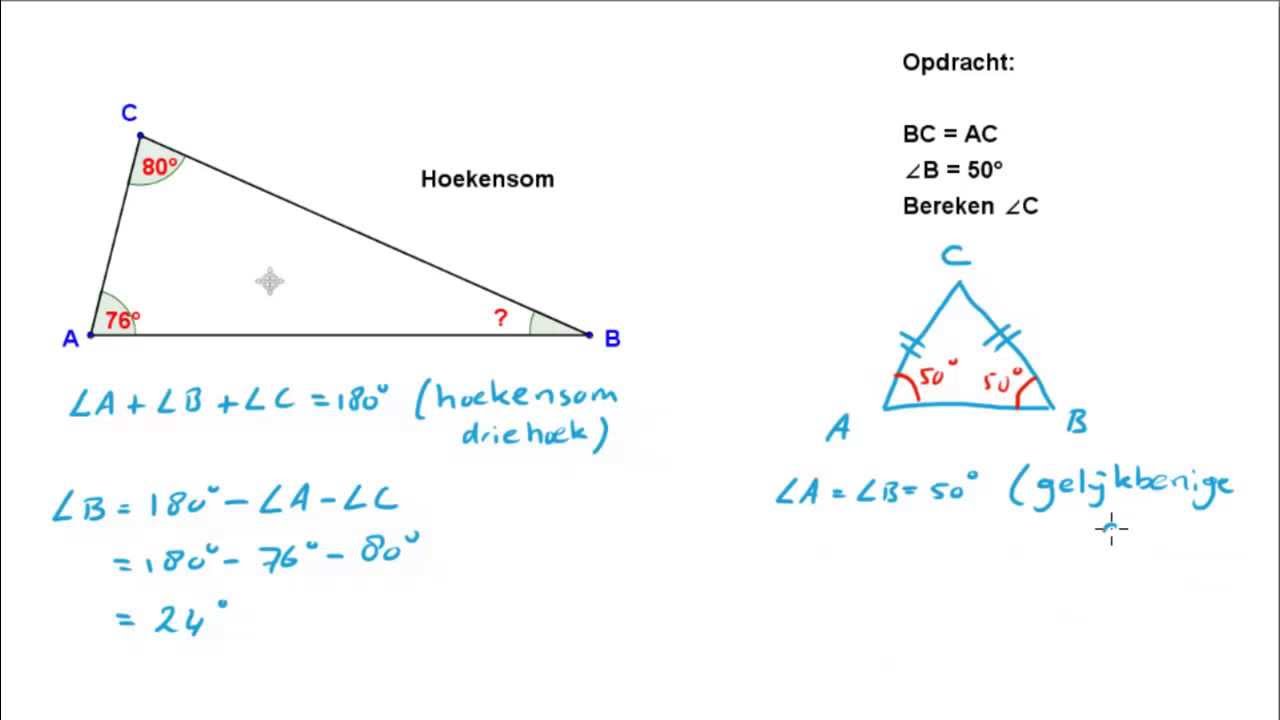
Een ontbrekende hoek vinden: Als je de grootte van twee hoeken van een driehoek kent, kun je de derde hoek berekenen door de bekende hoeken van 180 af te trekken. Bijvoorbeeld, als een driehoek hoeken van 60 en 80 graden heeft, dan is de derde hoek 180 - 60 - 80 = 40 graden.
Controleren of een figuur een driehoek kan zijn: Als je drie hoeken hebt, kun je controleren of ze daadwerkelijk een driehoek kunnen vormen door ze bij elkaar op te tellen. Als de som niet 180 graden is, dan kunnen ze geen driehoek vormen.
Problemen oplossen met onbekenden: Soms krijg je een probleem met een onbekende hoek, uitgedrukt als een variabele (bijvoorbeeld 'x'). Door de vergelijking 'x + (andere hoeken) = 180' op te stellen, kun je de waarde van x oplossen.

Voorbeeld:

Stel, je hebt een driehoek waarbij één hoek 90 graden is (een rechte hoek), en een andere hoek is 30 graden. Wat is de grootte van de derde hoek?

Oplossing:

We weten dat de som van de hoeken 180 graden is. Dus: 90 + 30 + x = 180. Vereenvoudig dit naar 120 + x = 180. Trek 120 van beide kanten af om x te vinden: x = 60. De derde hoek is dus 60 graden.

Dit principe is niet alleen nuttig voor het oplossen van schoolse problemen, maar ook voor praktische toepassingen in verschillende vakgebieden.

Toepassingen in de echte wereld

De som van de hoeken van een driehoek is niet alleen een abstract concept; het heeft talloze toepassingen in de echte wereld:

Architectuur en constructie: Architecten en ingenieurs gebruiken dit principe om structuren te ontwerpen en te bouwen die stabiel en evenwichtig zijn. Driehoeken zijn ongelooflijk sterke vormen, en het begrijpen van hun hoeken is essentieel voor het creëren van duurzame gebouwen en bruggen.
Navigatie: Navigators gebruiken trigonometrie, die gebaseerd is op de eigenschappen van driehoeken, om hun positie te bepalen en routes te plannen. Ze gebruiken bijvoorbeeld sterren en de horizon om hoeken te meten en hun locatie te berekenen.
Landmeten: Landmeters gebruiken driehoeken om land op te meten en kaarten te maken. Ze gebruiken instrumenten om hoeken en afstanden te meten, en passen vervolgens trigonometrie toe om de oppervlakte en omtrek van een stuk land te berekenen.
Grafisch ontwerp en game-ontwikkeling: Driehoeken zijn de bouwstenen van veel digitale beelden en 3D-modellen. Het begrijpen van hun eigenschappen is essentieel voor het creëren van realistische en visueel aantrekkelijke graphics.
Astronomie: Astronomen gebruiken triangulatie om de afstand tot sterren en andere hemellichamen te bepalen.

Denk er eens over na: de volgende keer dat je een brug bewondert, een gebouw bekijkt, of een videogame speelt, is de kans groot dat het principe van de som van de hoeken van een driehoek een rol heeft gespeeld in het ontwerp of de constructie ervan.

Conclusie

De som van de hoeken van een driehoek is altijd 180 graden. Dit is een fundamenteel principe van de geometrie met brede toepassingen in de echte wereld. Of je nu een student bent die worstelt met huiswerk, een professional die problemen oplost, of gewoon iemand die geïnteresseerd is in de wereld om je heen, het begrijpen van dit concept is essentieel.

Door te begrijpen *waarom* dit zo is, en door te leren hoe je dit principe kunt toepassen, kun je je probleemoplossende vaardigheden verbeteren en je waardering voor de schoonheid en kracht van de wiskunde verdiepen. Dus, de volgende keer dat je een driehoek ziet, onthoud dan: 180 graden – de magische formule die alles bij elkaar houdt!

Hopelijk heeft dit artikel je geholpen om dit belangrijke concept beter te begrijpen. Blijf leren en ontdekken, en wie weet welke andere wiskundige wonderen je zult ontdekken!