Hoeveel Grensvlakken Heeft Een Kubus

Laten we eerlijk zijn, wiskunde kan soms aanvoelen als een doolhof, vol met abstracte concepten en ingewikkelde formules. Velen van ons hebben in onze schooltijd wel eens gefrustreerd naar een meetkundig figuur gestaard, ons afvragend: "Waarom moet ik dit eigenlijk weten?" Vooral als het gaat om figuren zoals de kubus. Misschien denk je: "Wanneer ga ik ooit het aantal grensvlakken van een kubus in het dagelijks leven nodig hebben?" Toch zijn wiskundige concepten, hoe abstract ze ook lijken, de bouwstenen van de wereld om ons heen. Het begrijpen van deze concepten opent de deur naar een dieper inzicht in hoe dingen werken en hoe we problemen kunnen oplossen.

In dit artikel gaan we in op een ogenschijnlijk eenvoudige vraag: "Hoeveel grensvlakken heeft een kubus?" We zullen dit niet alleen beantwoorden, maar ook onderzoeken waarom deze kennis relevant is en hoe ze in verschillende contexten van pas kan komen. We proberen het zo helder en begrijpelijk mogelijk te maken, zodat iedereen, ongeacht zijn wiskundige achtergrond, mee kan doen.

De Kubus: Een Introductie

Voordat we het aantal grensvlakken tellen, is het belangrijk dat we allemaal hetzelfde beeld van een kubus voor ogen hebben. Een kubus is een driedimensionale geometrische figuur. Het is een bijzonder geval van een hexaëder, wat betekent dat het zes vlakken heeft. Maar er is meer:

Alle zijden zijn even lang. Dit betekent dat een kubus net zo hoog als breed als diep is.
Alle vlakken zijn vierkanten. Elk van de zes vlakken die een kubus vormen, is een perfect vierkant.
Alle hoeken zijn rechte hoeken. Elke hoek in een kubus is precies 90 graden.

Je ziet kubussen overal om je heen: dobbelstenen, suikerklontjes, sommige dozen en zelfs bepaalde gebouwen zijn kubusvormig. Deze alomtegenwoordigheid maakt het begrijpen van de eigenschappen van een kubus des te relevanter.

Hoeveel Grensvlakken Heeft Een Kubus? Het Antwoord

Het antwoord op de vraag "Hoeveel grensvlakken heeft een kubus?" is: zes.

Laten we eens kijken waar die zes vlakken zich bevinden:

Bovenkant
Onderkant
Voorkant
Achterkant
Linkerkant
Rechterkant

Probeer het je voor te stellen. Neem een dobbelsteen in je hand. Je kunt de bovenkant, de onderkant, de voorkant, de achterkant, de linkerkant en de rechterkant zien. Dat zijn zes vlakken in totaal!

Waarom Is Dit Relevant? Real-World Toepassingen

Het lijkt misschien triviaal, maar het begrijpen van het aantal grensvlakken van een kubus (en andere geometrische vormen) heeft verrassend veel praktische toepassingen:

Architectuur en Bouwkunde

Architecten en bouwkundigen gebruiken kennis van geometrie om gebouwen te ontwerpen en te construeren. Ze moeten de oppervlakte van verschillende vlakken berekenen om materialen te bepalen, de structurele integriteit te garanderen en de efficiëntie van de ruimte te optimaliseren. Denk aan het ontwerpen van een kubusvormig gebouw. De architect moet de oppervlakte van elk van de zes vlakken kennen om de benodigde hoeveelheid gevelbekleding te berekenen.

Verpakking

Bedrijven die producten verpakken, gebruiken geometrie om efficiënte en kosteneffectieve verpakkingsoplossingen te ontwerpen. Ze moeten de oppervlakte van de verpakking kennen om de benodigde hoeveelheid materiaal te bepalen en de verzendkosten te minimaliseren. Een kubusvormige doos is een veelvoorkomende verpakkingsvorm. Het kennen van het aantal en de afmetingen van de grensvlakken helpt bij het optimaliseren van het gebruik van karton.

Computergraphics en Game Development

In computertoepassingen, vooral in games en 3D-modellering, worden objecten vaak opgebouwd uit eenvoudige geometrische vormen zoals kubussen. Het begrijpen van de eigenschappen van een kubus is essentieel voor het creëren van realistische en interactieve omgevingen. Bij het modelleren van een kamer in een game kan een kubus gebruikt worden als basisvorm. Het aantal vlakken is cruciaal voor het correct renderen van de textuur en belichting.

Wiskunde en Wetenschap

Natuurlijk is het tellen van grensvlakken ook belangrijk in puur wiskundige en wetenschappelijke contexten. Het vormt de basis voor complexere berekeningen en concepten in meetkunde, calculus en natuurkunde. Het vormt een bouwsteen voor meer geavanceerde onderwerpen zoals oppervlakte-integralen en volumeberekeningen.

Counterpoints: Waarom Zou Dit Onbelangrijk Zijn?

Sommigen beweren misschien dat het tellen van de grensvlakken van een kubus een triviale bezigheid is, die weinig relevantie heeft voor het echte leven. Ze zouden kunnen zeggen dat computers en software deze berekeningen automatisch kunnen uitvoeren, waardoor menselijke kennis overbodig wordt. Hoewel het waar is dat technologie veel wiskundige taken heeft geautomatiseerd, is het essentieel om de onderliggende principes te begrijpen. Zonder een fundamenteel begrip van geometrie kunnen we de resultaten van de software niet kritisch beoordelen, problemen oplossen of innovatieve oplossingen bedenken.

Bovendien is het leren over de grensvlakken van een kubus een startpunt voor het begrijpen van complexere concepten. Het is een eerste stap op de weg naar een dieper begrip van de wereld om ons heen.

Een Praktisch Voorbeeld: Het Berekenen van Oppervlakte

Laten we een praktisch voorbeeld bekijken om te illustreren hoe de kennis van het aantal grensvlakken van een kubus van pas kan komen. Stel je voor dat je een kubusvormige doos hebt met een zijde van 10 centimeter. Je wilt weten hoeveel papier je nodig hebt om de doos volledig te bedekken.

Hier is hoe je het kunt berekenen:

Bereken de oppervlakte van één vlak. Aangezien elk vlak een vierkant is, is de oppervlakte gelijk aan zijde * zijde. In dit geval is dat 10 cm * 10 cm = 100 cm².
Vermenigvuldig de oppervlakte van één vlak met het aantal vlakken. Een kubus heeft 6 vlakken, dus de totale oppervlakte is 100 cm² * 6 = 600 cm².

Je hebt dus 600 vierkante centimeter papier nodig om de doos volledig te bedekken.

Het Gaat Niet Alleen Om Kubussen

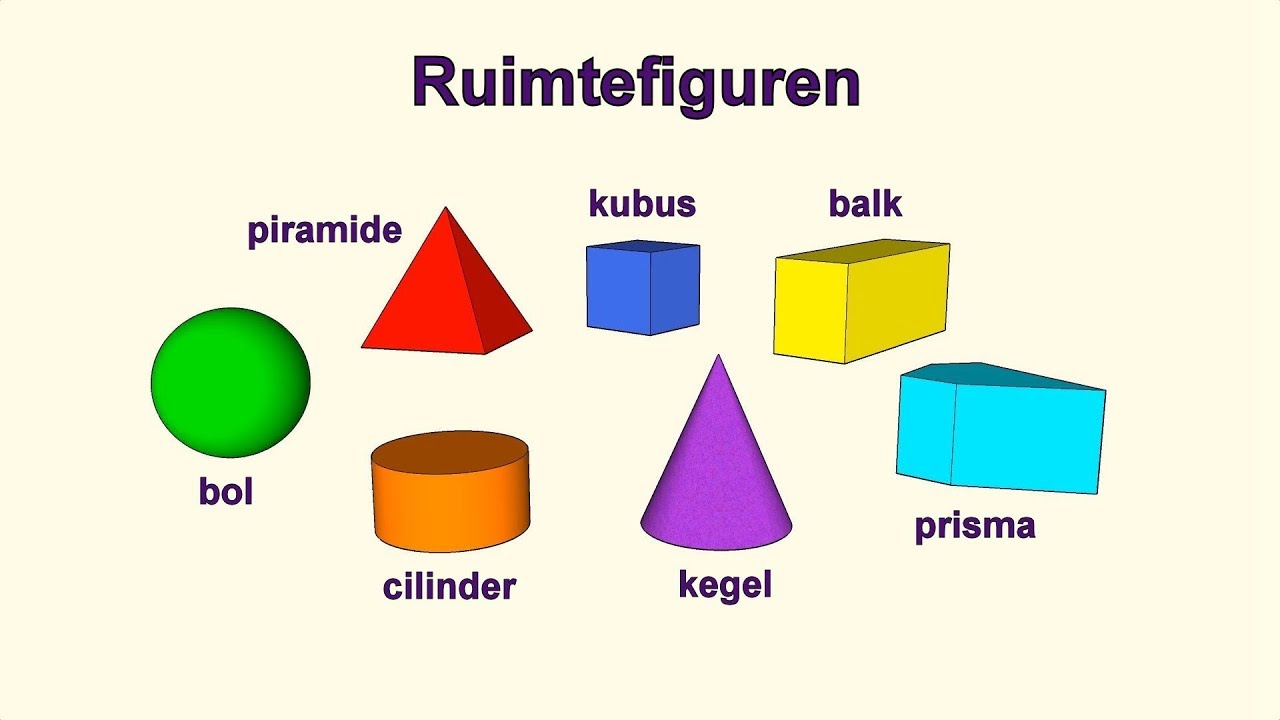
Het concept van grensvlakken is niet beperkt tot kubussen. Het is van toepassing op alle driedimensionale vormen, zoals prisma's, piramides, cilinders en kegels. Elk van deze vormen heeft een specifiek aantal en type grensvlakken. Het begrijpen van deze verschillen is essentieel voor het oplossen van een breed scala aan problemen in de wiskunde, wetenschap en engineering.

Hier zijn enkele voorbeelden:

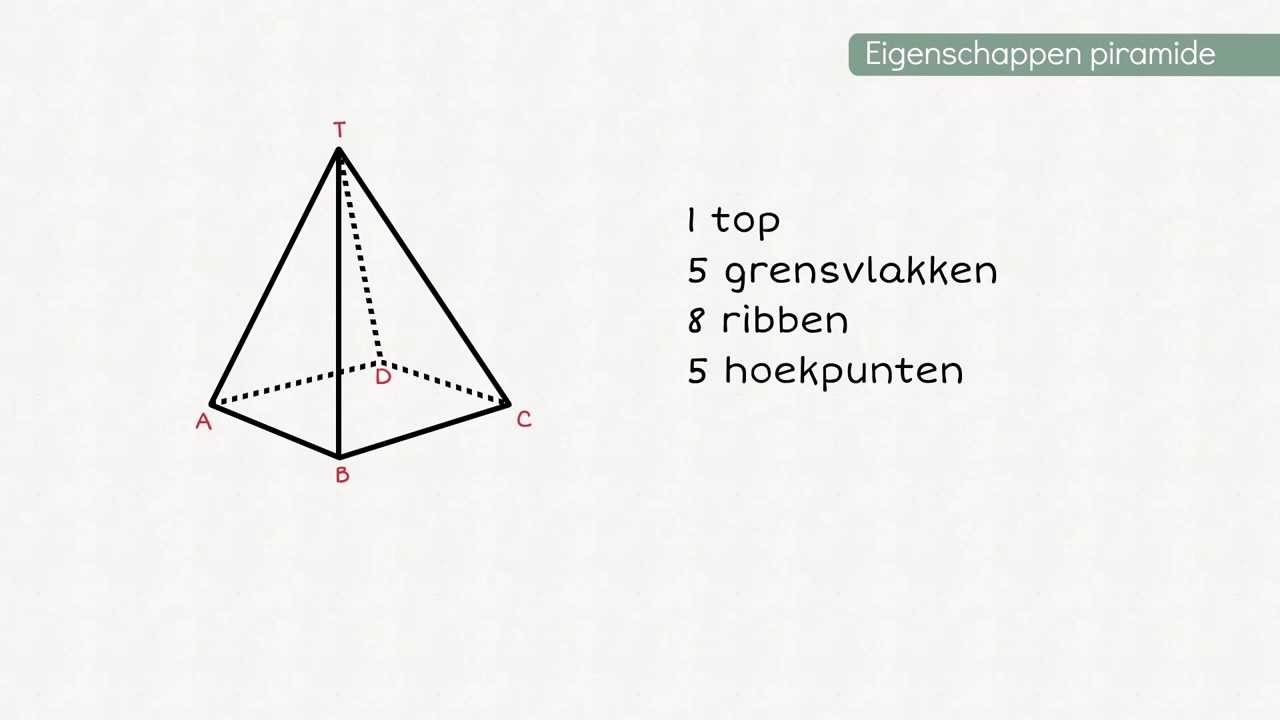
Een piramide met een vierkant grondvlak heeft 5 grensvlakken: 1 vierkant grondvlak en 4 driehoekige zijvlakken.
Een cilinder heeft 3 grensvlakken: 2 cirkelvormige vlakken (boven- en onderkant) en 1 gebogen vlak.
Een bol heeft 0 vlakke grensvlakken, maar wordt gedefinieerd door zijn oppervlak.

Door verschillende vormen te bestuderen en hun eigenschappen te begrijpen, kunnen we onze wiskundige intuïtie en probleemoplossende vaardigheden verbeteren.

De Volgende Stap: Verdieping van Je Kennis

Nu je weet hoeveel grensvlakken een kubus heeft en waarom dit relevant is, kun je je kennis verder verdiepen door:

Andere meetkundige vormen te bestuderen. Onderzoek de eigenschappen van prisma's, piramides, cilinders en kegels.
Oppervlakte en volume te berekenen. Oefen met het berekenen van de oppervlakte en het volume van verschillende objecten.
3D-modellering software te gebruiken. Experimenteer met 3D-modellering software om je ruimtelijk inzicht te verbeteren.
Wiskundige puzzels op te lossen. Daag jezelf uit met wiskundige puzzels die meetkundige concepten vereisen.

Conclusie

Het antwoord op de vraag "Hoeveel grensvlakken heeft een kubus?" is dus zes. Maar, zoals we hebben gezien, is het beantwoorden van deze eenvoudige vraag slechts het begin. Het begrijpen van de eigenschappen van een kubus opent de deur naar een dieper begrip van geometrie en haar talloze toepassingen in de wereld om ons heen. Van architectuur tot verpakking tot computertoepassingen, de kennis van meetkundige vormen is essentieel voor het oplossen van problemen en het creëren van innovatieve oplossingen.

Dus, de volgende keer dat je een kubus ziet, neem dan even de tijd om na te denken over de zes vlakken en de wiskundige principes die ten grondslag liggen aan zijn vorm. En wie weet, misschien ontdek je wel een nieuwe toepassing voor deze eenvoudige, maar krachtige, geometrische figuur.

Welke geometrische vorm ga jij nu bestuderen en welke toepassingen denk je te kunnen ontdekken?