Hoeveel Grensvlakken Heeft Een Piramide

Het antwoord op de vraag “Hoeveel grensvlakken heeft een piramide?” is verrassend complexer dan het op het eerste gezicht lijkt. Hoewel de basisgedachte eenvoudig is, schuilt de nuance in de verschillende soorten piramides en de wijze waarop we een ‘grensvlak’ definiëren. Deze tekst zal dieper ingaan op de eigenschappen van piramides en de factoren die het aantal grensvlakken beïnvloeden.

Wat is een piramide?

Een piramide is een driedimensionale meetkundige figuur die wordt gevormd door een veelhoek als basis en driehoekige zijvlakken die samenkomen in één punt, de top (apex) van de piramide. Het is essentieel te begrijpen dat de vorm van de basis de benaming van de piramide bepaalt. Zo hebben we:

• Een driehoekige piramide (ook wel tetraëder genoemd) met een driehoek als basis.
• Een vierkante piramide met een vierkant als basis.
• Een vijfhoekige piramide met een vijfhoek als basis.
• Enzovoort…

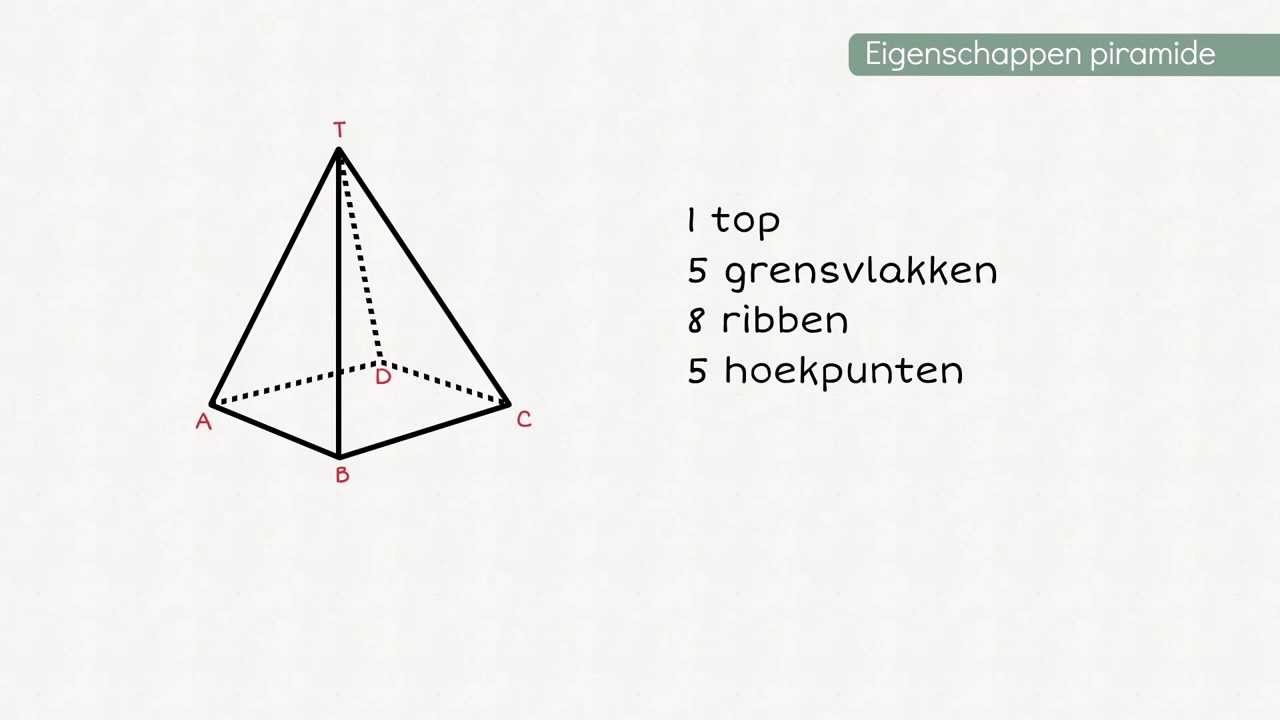
De grensvlakken van een piramide zijn de platte vlakken die de piramide begrenzen: de basis en de zijvlakken.

Het Aantal Grensvlakken Bepalen: De Basis en Zijvlakken

De cruciale factor bij het bepalen van het aantal grensvlakken is de vorm van de basis. Het aantal zijden van de basis is direct gekoppeld aan het aantal driehoekige zijvlakken. Laten we enkele voorbeelden bekijken:

Driehoekige Piramide (Tetraëder)

Een driehoekige piramide, ook bekend als een tetraëder, heeft een driehoek als basis. Dit betekent dat het drie driehoekige zijvlakken heeft. Tel daarbij de basis (zelf ook een driehoek) op, en je komt tot een totaal van vier grensvlakken. Dit maakt de tetraëder een bijzonder geval, omdat alle vlakken congruent (gelijkvormig en even groot) kunnen zijn. Wanneer alle zijden even lang zijn, spreken we van een regelmatige tetraëder, een van de vijf platonische lichamen.

Vierkante Piramide

Een vierkante piramide heeft een vierkant als basis. Dit betekent dat het vier driehoekige zijvlakken heeft. Tel de vierkante basis erbij, en je hebt in totaal vijf grensvlakken. Denk aan de piramides van Gizeh in Egypte, die iconische voorbeelden zijn van vierkante piramides.

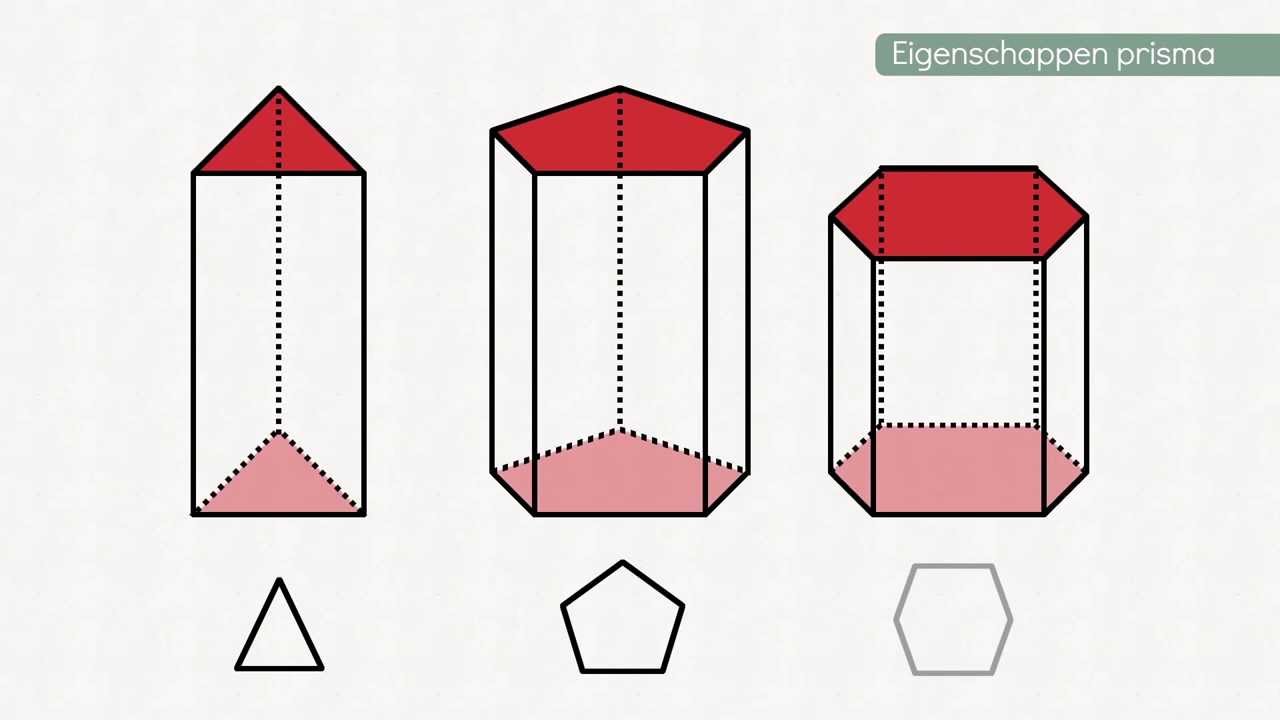
Vijfhoekige Piramide

Een vijfhoekige piramide heeft een vijfhoek als basis en dus vijf driehoekige zijvlakken. Samen met de basis resulteert dit in zes grensvlakken. Deze vorm is minder gebruikelijk in de architectuur, maar komt wel voor in kristallijne structuren en theoretische modellen.

De Algemene Formule

We kunnen een algemene formule afleiden om het aantal grensvlakken van een piramide te berekenen:

Aantal grensvlakken = Aantal zijden van de basis + 1

De "+ 1" staat voor de basis zelf, die ook een grensvlak is.

Dus, een piramide met een n-hoekige basis heeft n + 1 grensvlakken.

Regelmatige en Onregelmatige Piramides

Het is belangrijk om te vermelden dat de hierboven besproken principes gelden voor zowel regelmatige als onregelmatige piramides. Een regelmatige piramide heeft een regelmatige veelhoek als basis (alle zijden en hoeken gelijk) en de top bevindt zich loodrecht boven het middelpunt van de basis. Een onregelmatige piramide heeft een onregelmatige veelhoek als basis, of de top bevindt zich niet loodrecht boven het middelpunt van de basis. Desondanks verandert dit niets aan het feit dat het aantal grensvlakken nog steeds wordt bepaald door het aantal zijden van de basis plus één.

Een voorbeeld van een onregelmatige piramide is een piramide waarbij de basis een ongelijkzijdige driehoek is en de top niet recht boven het zwaartepunt van de basis ligt. Het heeft nog steeds 4 grensvlakken, maar de driehoekige zijvlakken zijn niet congruent.

Piramide in de Praktijk: Architectuur en Natuur

Piramides zijn niet alleen abstracte meetkundige objecten, ze komen ook veel voor in de wereld om ons heen. De piramides van Gizeh zijn misschien wel de meest bekende voorbeelden van mensgemaakte piramides. Deze imposante bouwwerken demonstreren de stabiliteit en structurele kracht van piramidevormen. Minder bekende maar even interessante voorbeelden zijn de piramides die in diverse culturen zijn gebouwd, zoals de Maya-piramides in Midden-Amerika en de Nubische piramides in Soedan.

Ook in de natuur komen piramidevormen voor. Sommige bergtoppen benaderen een piramidevorm, en kristallen kunnen ook piramidale structuren vertonen. De vorm van bepaalde virussen, bijvoorbeeld, is ook icosahedraal, wat kan worden gezien als een soort piramide met veel zijvlakken.

Conclusie

Samenvattend: het aantal grensvlakken van een piramide is afhankelijk van het aantal zijden van de basis. De formule Aantal grensvlakken = Aantal zijden van de basis + 1 geeft een helder antwoord op de vraag. Of het nu gaat om een regelmatige of onregelmatige piramide, deze regel blijft van kracht. Van de majestueuze piramides van Gizeh tot microscopische kristalstructuren, de piramidevorm is een fascinerend voorbeeld van meetkunde in actie.

Om je begrip verder te verdiepen, raden we aan om zelf met verschillende soorten piramides te experimenteren. Maak papieren modellen of gebruik 3D-modelleringssoftware om de verschillende vormen te visualiseren en zelf te tellen! Het zelf doen is vaak de beste manier om de principes van meetkunde te begrijpen en te onthouden.