Hoeveel Hoekpunten Heeft Een Kegel

Ben je ooit in de war geraakt door geometrische vormen? Vooral kegels kunnen soms lastig zijn, zeker als het gaat om hun hoekpunten. Je bent niet de enige! Veel mensen worstelen met deze vraag, omdat het antwoord misschien niet zo voor de hand ligt als je denkt. We gaan dit nu helder voor je maken.

Wat is een Hoekpunt Eigenlijk?

Laten we beginnen met de basis. Een hoekpunt, ook wel een vertex genoemd, is een punt waar twee of meer lijnen, lijnensegmenten of randen samenkomen. Denk aan de scherpe punt van een driehoek of de hoeken van een vierkant. Het is een essentieel onderdeel van de geometrie en helpt ons vormen te definiëren en te onderscheiden.

Hoe Zit het met Kegels?

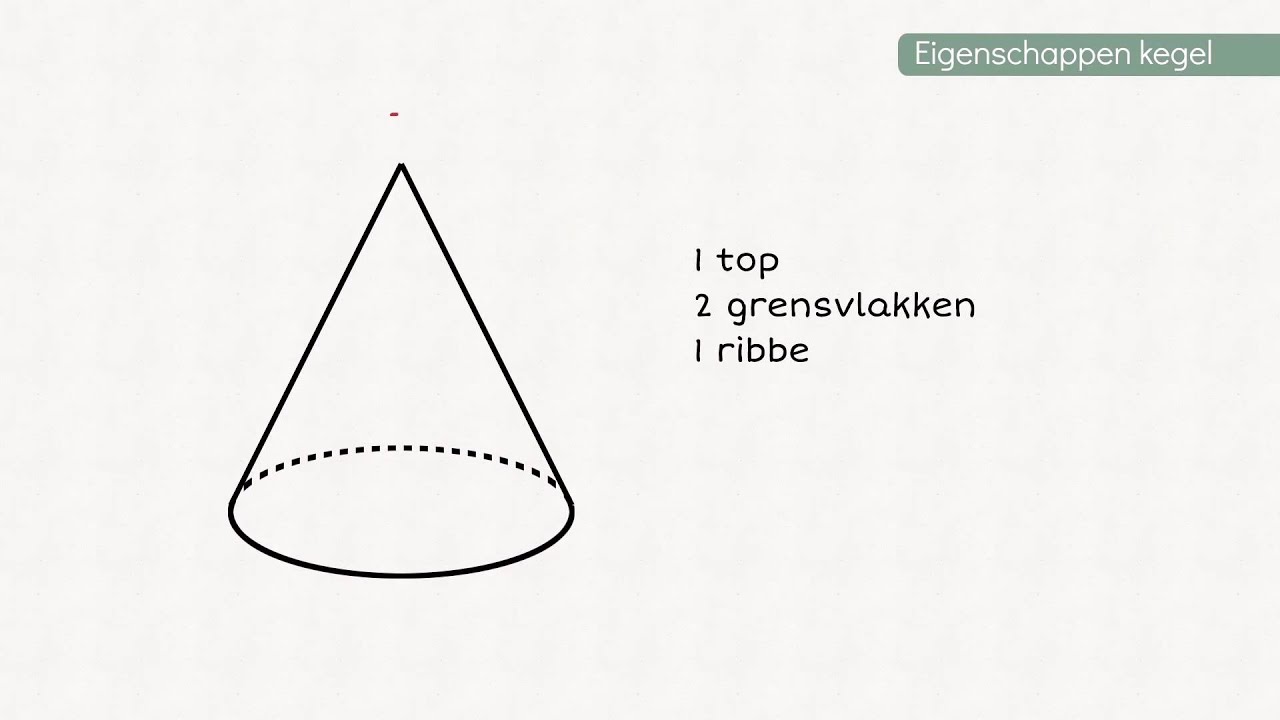
Nu komen we bij de crux van de zaak: de kegel. Een kegel is een driedimensionale geometrische vorm die zich vanuit een plat vlak (een cirkel) geleidelijk toewerkt naar een enkel punt, de top of apex. Denk aan een ijshoorntje, een verkeerskegel, of de punt van een kerstboom. De verwarring ontstaat vaak doordat men zich afvraagt of een kegel meerdere hoekpunten heeft, of slechts één.

Het Verwarrende Antwoord: 1 Hoekpunt

Het antwoord is vrij eenvoudig: een kegel heeft één hoekpunt. Namelijk de top of de apex. Dit is het punt waar alle lijnen vanuit de cirkelvormige basis samenkomen. Er zijn geen andere "hoeken" zoals je die zou vinden in een kubus of een piramide.

Waarom de Verwarring? De verwarring komt vaak voort uit de basis van de kegel: een cirkel. Cirkels hebben geen hoekpunten in de traditionele zin van het woord. Ze zijn immers rond en hebben geen scherpe hoeken. De kegel combineert echter deze ronde basis met een duidelijk gedefinieerd punt, de top.

De Onderdelen van een Kegel: Meer dan Alleen een Hoekpunt

Hoewel de kegel maar één hoekpunt heeft, is het nuttig om de andere onderdelen te kennen:

Basis: De cirkelvormige platte kant van de kegel.
Mantel: Het gebogen oppervlak dat de basis verbindt met de top.
Hoogte: De loodrechte afstand van de top tot het middelpunt van de basis.
Straal: De afstand van het middelpunt van de basis tot de rand.
Schuine zijde (L): De afstand van de top tot een punt op de rand van de basis.

Deze onderdelen samen bepalen de vorm en de eigenschappen van de kegel. Het is belangrijk ze te begrijpen om de kegel in zijn geheel te kunnen analyseren.

Praktische Voorbeelden en Toepassingen

Kegels kom je overal tegen in het dagelijks leven en in de wetenschap. Hier zijn een paar voorbeelden:

Architectuur: Kegelvormige daken zijn te zien op torens en gebouwen, vaak vanwege hun structurele sterkte en hun vermogen om water af te voeren. Denk bijvoorbeeld aan de torenspitsen van sommige kerken.
Verkeer: Verkeerskegels worden gebruikt om weggebruikers te waarschuwen en om gebieden af te bakenen tijdens wegwerkzaamheden. Hun felgekleurde uiterlijk en kegelvorm zorgen voor een goede zichtbaarheid.
Wiskunde en Natuurkunde: Kegels spelen een rol in verschillende wiskundige formules, zoals het berekenen van het volume en de oppervlakte. In de natuurkunde worden ze gebruikt bij de studie van beweging en zwaartekracht.
Voeding: Denk aan ijshoorntjes! De kegelvorm maakt het makkelijk om ijs te serveren en te eten.

De Formule van het Volume van een Kegel

Om nog even dieper in de wiskunde te duiken, laten we eens kijken naar de formule voor het volume van een kegel:

V = (1/3)πr²h

Waar:

V = Volume
π (pi) ≈ 3.14159
r = Straal van de basis
h = Hoogte van de kegel

Deze formule laat zien hoe de straal van de basis en de hoogte van de kegel direct van invloed zijn op het totale volume. Begrijpen van deze formule is essentieel in veel technische en wetenschappelijke vakgebieden.

Waarom Is Dit Belangrijk?

Misschien vraag je je af waarom het belangrijk is om te weten hoeveel hoekpunten een kegel heeft. Nou, het begrijpen van basis geometrische concepten is cruciaal voor:

Ruimtelijk inzicht: Het helpt je objecten in 3D-ruimte beter te visualiseren en te begrijpen.
Probleemoplossing: Veel problemen in de wetenschap, techniek en architectuur vereisen een goed begrip van geometrische vormen.
Wiskundige vaardigheden: Het is een fundamentele bouwsteen voor meer geavanceerde wiskunde.

Door de basisbeginselen van geometrie te leren, leg je een solide basis voor toekomstige successen op verschillende gebieden.

Tips om Geometrie Makkelijker te Maken

Geometrie kan soms intimiderend zijn, maar hier zijn een paar tips om het makkelijker te maken:

Visualiseer: Gebruik modellen, tekeningen of online simulaties om de vormen beter te begrijpen.
Oefen: Maak veel oefenopgaven om de formules en concepten te beheersen.
Zoek hulp: Aarzel niet om je leraar, een tutor of online bronnen te raadplegen als je vastzit.
Maak het leuk: Probeer geometrische puzzels of games om het leren leuker te maken.

Conclusie: De Kegel Ontmaskerd!

Dus, om het nog eens samen te vatten: een kegel heeft één hoekpunt, namelijk de top. Hoewel de cirkelvormige basis geen hoekpunten heeft, is de top het duidelijke punt waar de lijnen van de mantel samenkomen. Door de onderdelen van een kegel te begrijpen en de praktische toepassingen ervan te kennen, kun je met meer vertrouwen geometrische problemen aanpakken.

Onthoud dat geometrie niet eng hoeft te zijn. Met de juiste uitleg en wat oefening kan iedereen de basisprincipes leren en waarderen. Dus ga ervoor, ontdek de wereld van de vormen en geniet van het leerproces! Misschien ga je de wereld wel met andere ogen bekijken.