Hoeveel Hoekpunten Heeft Een Kubus

De vraag "Hoeveel hoekpunten heeft een kubus?" lijkt eenvoudig, maar het antwoord opent de deur naar een breder begrip van geometrische vormen en hun eigenschappen. In dit artikel duiken we dieper in de kubus, onderzoeken we de hoekpunten, en bekijken we de relevantie van deze kennis.

Wat is een Hoekpunt?

Laten we beginnen met de basis. Een hoekpunt, in de context van geometrie, is het punt waar twee of meer lijnen, lijnsegmenten of randen samenkomen. Stel je voor: het is de 'hoek' van een figuur. In tweedimensionale (2D) vormen zoals een vierkant of een driehoek, noemen we ze simpelweg hoeken. Maar in driedimensionale (3D) vormen, zoals onze focus – de kubus – spreken we specifiek van hoekpunten.

Het Belang van Hoekpunten

Hoekpunten zijn cruciaal voor de definitie en het begrip van een object. Ze bepalen de vorm, de structuur en de eigenschappen van de figuur. Het aantal hoekpunten, samen met het aantal zijvlakken en ribben (lijnen die de hoekpunten verbinden), helpt ons bij het classificeren en analyseren van verschillende polygonen en veelvlakken.

De Kubus: Een Definitie

Een kubus is een driedimensionaal geometrisch object dat wordt gedefinieerd door de volgende eigenschappen:

Het is een regelmatig veelvlak. Dit betekent dat alle zijvlakken identiek zijn.
Alle zijvlakken zijn vierkanten.
Alle ribben (de lijnen die de hoekpunten verbinden) zijn even lang.
De hoeken tussen de zijvlakken zijn allemaal rechte hoeken (90 graden).

Vanwege deze eigenschappen is de kubus een van de meest fundamentele en eenvoudigste 3D-vormen, wat het een ideaal startpunt maakt voor het bestuderen van geometrie.

Hoeveel Hoekpunten Heeft een Kubus?

Nu komen we bij de kern van de vraag: een kubus heeft acht hoekpunten. Denk eraan als de acht 'punten' of 'hoeken' van de kubus waar de randen samenkomen. Om dit te visualiseren, stel je een dobbelsteen voor. Elke 'punt' van de dobbelsteen is een hoekpunt.

Het Tellen van de Hoekpunten

Een manier om het aantal hoekpunten te bevestigen is door ze letterlijk te tellen. Stel je een kubus voor, begin bij één hoekpunt en tel systematisch rond de kubus. Je zult merken dat er vier hoekpunten aan de bovenkant zijn en vier hoekpunten aan de onderkant, wat resulteert in een totaal van acht.

Euler's Formule

Er is een wiskundige formule die het verband legt tussen het aantal hoekpunten (V), ribben (E), en zijvlakken (F) van een veelvlak: V - E + F = 2. Dit staat bekend als de Euler's formule. Laten we deze formule gebruiken om te controleren of we het juiste aantal hoekpunten hebben gevonden.

Een kubus heeft 6 zijvlakken (F = 6) en 12 ribben (E = 12). Als we de Euler's formule toepassen, krijgen we:

V - 12 + 6 = 2

V - 6 = 2

V = 8

De formule bevestigt dat een kubus inderdaad 8 hoekpunten heeft.

De Relevantie in de Praktijk

Het begrip van hoekpunten, ribben en zijvlakken is niet alleen belangrijk in de abstracte wiskunde, maar ook in verschillende praktische toepassingen.

3D Modellering en Computer Graphics

In 3D-modellering en computer graphics zijn hoekpunten de basisbouwstenen van alle modellen. Elk object wordt opgebouwd uit een netwerk van hoekpunten die met ribben en zijvlakken zijn verbonden. Het aantal hoekpunten en hun posities bepalen de vorm en de details van het model. Games, animatiefilms en architecturale visualisaties maken allemaal intensief gebruik van deze principes.

Architectuur en Bouwkunde

Architecten en bouwkundigen gebruiken geometrische vormen, waaronder de kubus en afgeleiden ervan, in hun ontwerpen. Het begrijpen van de eigenschappen van deze vormen, inclusief het aantal hoekpunten, is essentieel voor de structurele integriteit en het esthetische ontwerp van gebouwen. Denk aan de fundering van een gebouw, de hoeken van een kamer, of de constructie van een dak. Deze elementen zijn allemaal gebaseerd op geometrische principes.

Verpakking en Logistiek

De kubusvorm is ook wijdverspreid in de verpakkingsindustrie en logistiek. Dozen en containers zijn vaak kubusvormig of rechthoekig van vorm, wat een efficiënte benutting van de ruimte mogelijk maakt. Het ontwerp van deze verpakkingen houdt rekening met het aantal hoekpunten en de stevigheid van de constructie om producten veilig te transporteren.

Spelletjes en Puzzels

De kubus vormt de basis voor veel spelletjes en puzzels, zoals de Rubik's kubus. Het begrip van de geometrie van de kubus is essentieel om deze puzzels op te lossen. De hoekpunten, randen en zijvlakken zijn allemaal relevant voor de bewegingen en de oplossingen.

Andere Polyhedra en hun Hoekpunten

Om het concept verder te illustreren, kunnen we het aantal hoekpunten van andere veelvlakken vergelijken met dat van een kubus:

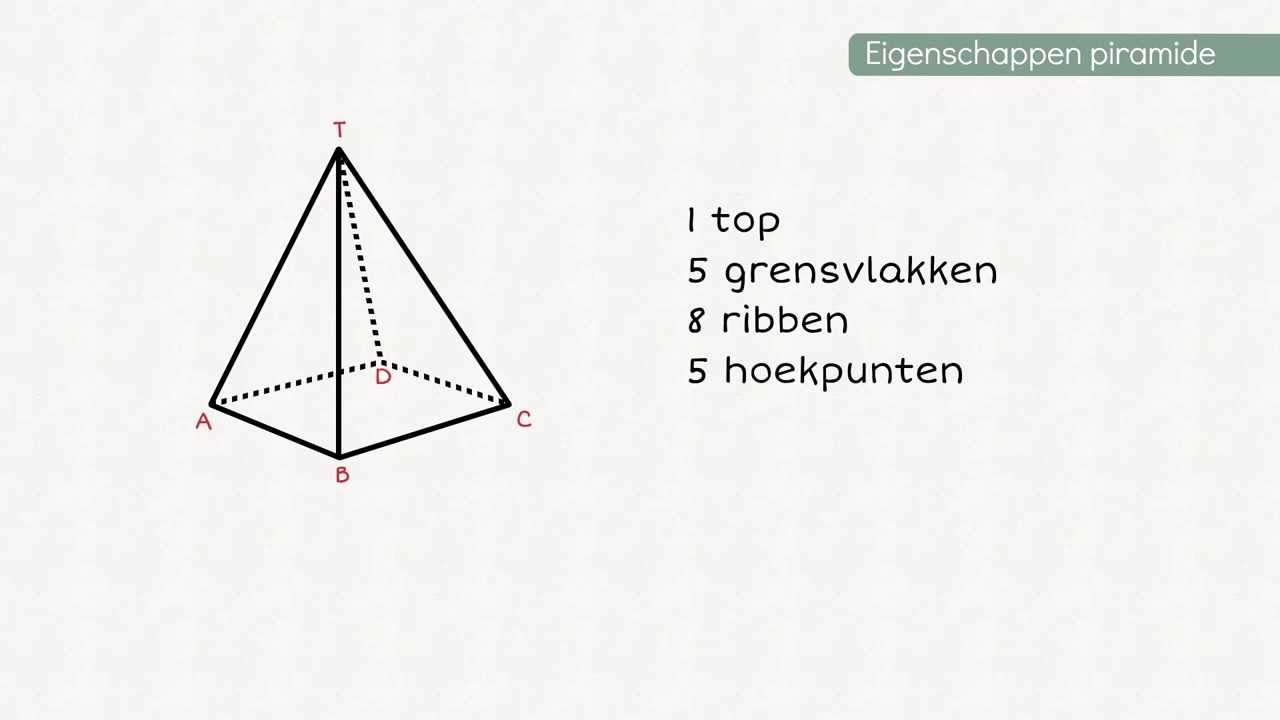
Tetraëder (piramide met driehoekige basis): 4 hoekpunten
Octaëder: 6 hoekpunten
Dodecaëder: 20 hoekpunten
Icosaëder: 12 hoekpunten

Elk van deze vormen heeft een uniek aantal hoekpunten, ribben en zijvlakken, en volgt de Euler's formule. Het bestuderen van deze verschillende vormen helpt ons om de algemene principes van geometrie beter te begrijpen.

Conclusie

De kubus, met zijn acht hoekpunten, is een fundamentele geometrische vorm met een breed scala aan toepassingen in de praktijk. Of het nu gaat om 3D-modellering, architectuur, verpakkingen of spelletjes, het begrip van de eigenschappen van de kubus is essentieel. Het tellen van de hoekpunten is meer dan alleen een wiskundige oefening; het is een stap naar het begrijpen van de wereld om ons heen. Dus, de volgende keer dat je een kubus ziet, denk dan aan de acht hoekpunten die de basis vormen van deze veelzijdige vorm.

Wil je meer leren over geometrie en 3D vormen? Zoek online naar bronnen over veelvlakken, Euler's formule, en 3D modellering software. Experimenteer met het bouwen van je eigen geometrische vormen en ontdek de fascinerende wereld van de wiskunde!