Hoeveel Hoekpunten Heeft Een Piramide

Heb je je ooit afgevraagd hoe de majestueuze piramides van Egypte zijn gebouwd? Of wellicht de vorm van een tent, een dak, of zelfs een stuk speelgoed opgemerkt dat verdacht veel op een piramide lijkt? Het antwoord op die vragen begint vaak met een fundamenteel begrip: de basisvorm en de eigenschappen van een piramide. Eén van die fundamentele eigenschappen is het aantal hoekpunten. Laten we dat eens nader bekijken. Het lijkt misschien een simpele vraag, maar het antwoord onthult interessante details over de geometrie achter deze iconische vorm.

Misschien vind je geometrie ingewikkeld, een vak vol formules en abstracte concepten. Maar geometrie is overal om ons heen. Het zit in de architectuur van gebouwen, de lay-out van steden en zelfs in de natuur. Het begrijpen van basisvormen zoals piramides kan ons helpen de wereld om ons heen beter te begrijpen. En het is veel minder angstaanjagend dan je misschien denkt!

Wat is een hoekpunt?

Laten we beginnen bij de basis: wat is een hoekpunt precies? Een hoekpunt is simpelweg een punt waar twee of meer lijnen samenkomen. Denk aan de hoek van een kubus, de punt van een ster, of de top van een berg. In het platte vlak, bij een vierkant bijvoorbeeld, zijn de hoekpunten de vier "punten" waar de zijden elkaar kruisen.

In 3D-figuren, zoals piramides, zijn de hoekpunten ook de punten waar de ribben (de lijnen die de vlakken begrenzen) samenkomen. Het is dus letterlijk een "hoek" in de ruimte.

Hoeveel hoekpunten heeft een piramide?

Nu komen we tot de kernvraag: hoeveel hoekpunten heeft een piramide? Het antwoord is niet altijd hetzelfde! Het aantal hoekpunten hangt namelijk af van de vorm van het grondvlak van de piramide.

De basis bepaalt het aantal hoekpunten

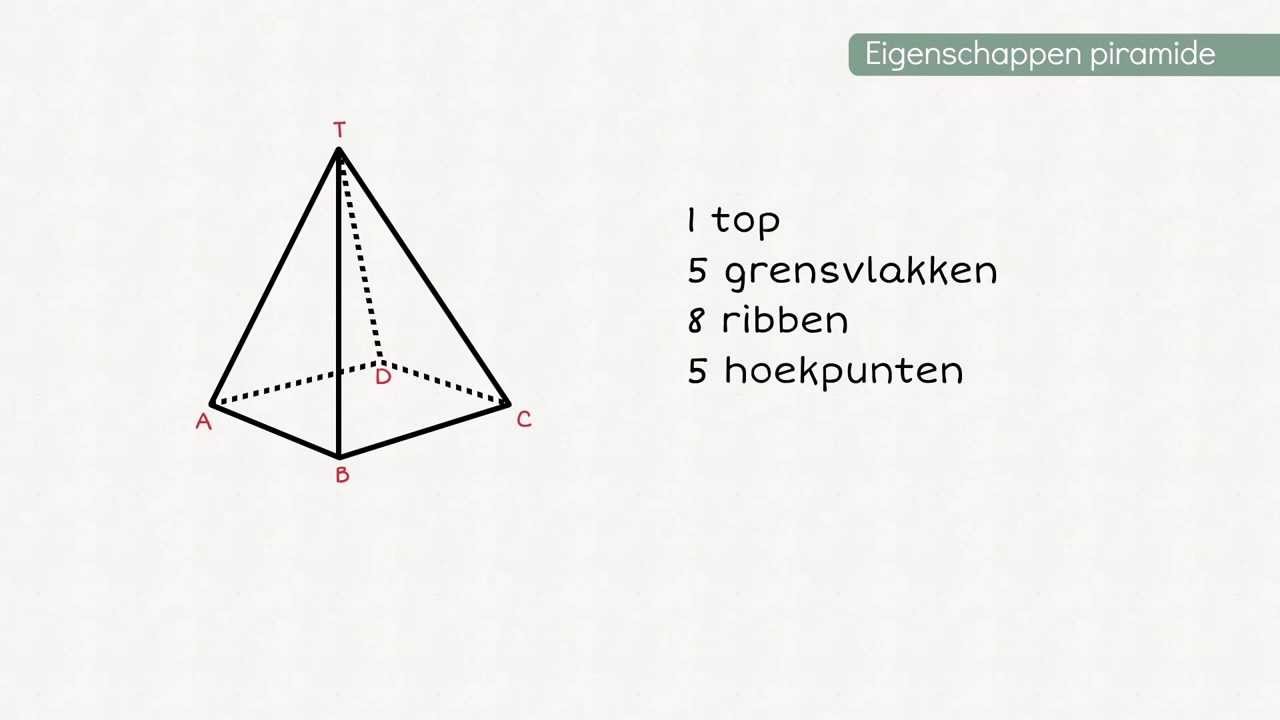
Het grondvlak is het vlak aan de onderkant van de piramide. Dit kan een driehoek, vierkant, vijfhoek, zeshoek, of zelfs een figuur met nog meer zijden zijn. Elk hoekpunt van het grondvlak, plus de top (de punt bovenaan de piramide), draagt bij aan het totale aantal hoekpunten.

• Driehoekige piramide (tetraëder): Een driehoekige piramide, ook wel een tetraëder genoemd, heeft een driehoek als grondvlak. Daarom heeft hij vier hoekpunten: drie op het grondvlak en één top.
• Vierkante piramide: Een vierkante piramide heeft een vierkant als grondvlak. Dus hij heeft vijf hoekpunten: vier op het grondvlak en één top.
• Vijfhoekige piramide: Een vijfhoekige piramide heeft een vijfhoek als grondvlak. Hij heeft dus zes hoekpunten: vijf op het grondvlak en één top.
• Zeshoekige piramide: Een zeshoekige piramide heeft een zeshoek als grondvlak. Hij heeft zeven hoekpunten: zes op het grondvlak en één top.

Je ziet een patroon! Voor elke extra zijde in het grondvlak, komt er één hoekpunt bij. Algemeen geldt: een piramide met een *n*-hoekig grondvlak heeft *n* + 1 hoekpunten.

Waarom is dit belangrijk?

Misschien denk je: "Leuk al die hoekpunten, maar wat heb ik eraan?". Het begrijpen van de geometrische eigenschappen van piramides is belangrijk in veel verschillende vakgebieden:

• Architectuur: Architecten gebruiken piramidevormen in gebouwen en structuren vanwege hun stabiliteit en esthetische waarde. De juiste berekening van hoekpunten en vlakken is cruciaal voor de structurele integriteit.
• Engineering: Ingenieurs gebruiken geometrische principes om bruggen, tunnels en andere constructies te ontwerpen.
• Grafisch ontwerp: Grafisch ontwerpers gebruiken 3D-modellen van piramides voor visualisaties, games en animaties.
• Wiskunde en wetenschap: Het bestuderen van piramides draagt bij aan het begrijpen van ruimtelijke figuren en geometrische principes in het algemeen.
• Kunst: Kunstenaars gebruiken piramidevormen in hun sculpturen en installaties. Denk aan de piramides van glas in de binnenplaats van het Louvre in Parijs.

Het is dus meer dan alleen een schoolvraag. Het is een fundamenteel begrip dat terugkomt in verschillende disciplines.

Veelgemaakte fouten en misverstanden

Een veelgemaakte fout is om te denken dat alle piramides vierkant zijn. Zoals we hebben gezien, kan het grondvlak van een piramide elke vorm hebben. Een andere veelvoorkomende fout is om het verschil tussen een piramide en een prisma te vergeten. Een prisma heeft twee identieke grondvlakken en rechthoekige zijvlakken, terwijl een piramide slechts één grondvlak en driehoekige zijvlakken heeft.

Sommige mensen verwarren een piramide ook met een kegel. Hoewel een kegel op een piramide lijkt, heeft een kegel een cirkelvormig grondvlak en geen hoekpunten op het grondvlak zelf, afgezien van het punt waar het cirkelvormige grondvlak eindigt. Het is dus belangrijk de definitie van een piramide helder te hebben.

Het belang van ruimtelijk inzicht

Het begrijpen van het aantal hoekpunten van een piramide is een onderdeel van het ontwikkelen van ruimtelijk inzicht. Ruimtelijk inzicht is het vermogen om objecten in 3D te visualiseren en te manipuleren. Het is een belangrijke vaardigheid voor veel beroepen, maar ook voor alledaagse taken zoals het inpakken van een doos of het navigeren in een nieuwe omgeving.

Het oefenen met geometrische figuren, zoals piramides, helpt bij het ontwikkelen van dit ruimtelijk inzicht. Het is alsof je je hersenen traint om in 3D te denken.

Alternatieve perspectieven en tegenargumenten

Sommige mensen beweren dat het bestuderen van eenvoudige geometrische vormen zoals piramides irrelevant is in een tijdperk van complexe wiskunde en AI. Ze stellen dat de focus moet liggen op geavanceerdere concepten en technologieën. Hoewel het belangrijk is om op de hoogte te blijven van de nieuwste ontwikkelingen, is een solide basis in fundamentele principes essentieel. Zelfs de meest geavanceerde algoritmen zijn gebaseerd op fundamentele wiskundige concepten, waaronder geometrie. Bovendien, het leren denken en problemen oplossen met behulp van eenvoudige modellen, zoals piramides, bouwt een essentiële denkvaardigheid op.

Anderen beweren dat de nadruk op het aantal hoekpunten te schools is en weinig te maken heeft met de praktische toepassing van piramides. Echter, het begrijpen van de geometrische eigenschappen van een piramide is de basis voor het begrijpen van de structurele eigenschappen. Een architect die een piramidevormig dak ontwerpt, moet precies weten hoe de hoeken en vlakken samenkomen om de stabiliteit te garanderen. Dus, ook al lijkt het een abstract concept, het heeft directe praktische relevantie.

Oefening baart kunst

Het beste manier om het aantal hoekpunten van een piramide te onthouden, is door te oefenen. Probeer zelf piramides te tekenen met verschillende grondvlakken. Tel de hoekpunten. Gebruik bouwstenen of klei om piramides te maken. Zoek piramidevormige objecten in je omgeving. Hoe meer je met de vorm bezig bent, hoe beter je het zult begrijpen.

Je kunt ook online bronnen gebruiken, zoals interactieve 3D-modellen van piramides. Met deze modellen kun je de piramide vanuit verschillende hoeken bekijken en de hoekpunten tellen. Er zijn ook educatieve games en apps die je kunnen helpen geometrische concepten te leren.

Conclusie

Het aantal hoekpunten van een piramide is afhankelijk van de vorm van het grondvlak. Een piramide met een *n*-hoekig grondvlak heeft *n* + 1 hoekpunten. Dit fundamentele begrip is belangrijk voor verschillende vakgebieden, van architectuur tot grafisch ontwerp. Het ontwikkelen van ruimtelijk inzicht door het bestuderen van geometrische figuren zoals piramides is een waardevolle vaardigheid.

Nu je dit weet, kijk eens om je heen. Kun je piramidevormen herkennen in je omgeving? En zo ja, hoeveel hoekpunten hebben ze?