Hoeveel Hoekpunten Heeft Een Prisma

Het begrijpen van de eigenschappen van geometrische vormen is essentieel, niet alleen voor studenten wiskunde, maar ook voor iedereen die zich bezighoudt met architectuur, design en andere praktische toepassingen. Een van de meest voorkomende en interessante vormen is het prisma. Een veelgestelde vraag over prisma's is: hoeveel hoekpunten heeft een prisma? Het antwoord is niet zo eenvoudig als een enkel getal, omdat het aantal hoekpunten afhangt van het type prisma in kwestie. Dit artikel gaat dieper in op deze vraag en onderzoekt de factoren die het aantal hoekpunten bepalen.

Wat is een Prisma?

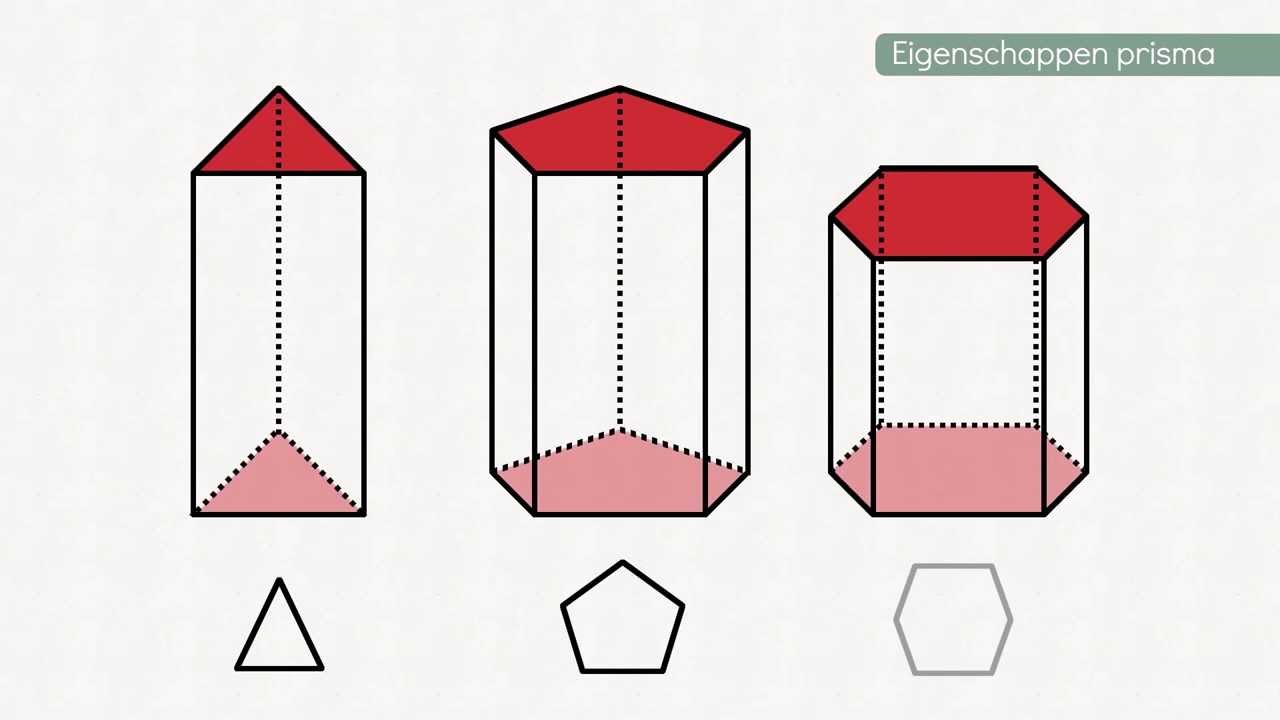
Laten we beginnen met een definitie: Een prisma is een driedimensionale geometrische vorm met twee identieke en parallelle basissen, verbonden door rechthoekige vlakken (of parallellogrammen, in het geval van een schuin prisma). De basissen kunnen elke veelhoek zijn, zoals een driehoek, vierkant, vijfhoek, enzovoort. De zijvlakken, die de basissen verbinden, zijn altijd rechthoeken (of parallellogrammen). Een belangrijk kenmerk is dat de doorsnede parallel aan de basis overal hetzelfde is.

Belangrijke Termen:

• Basis: De twee identieke en parallelle veelhoeken.
• Zijvlakken: De rechthoekige (of parallellogramvormige) vlakken die de basissen verbinden.
• Hoekpunt: Een punt waar twee of meer lijnen of randen samenkomen. Het zijn de "hoeken" van de vorm.
• Ribbe: Een lijnstuk waar twee vlakken samenkomen.

De Invloed van de Basis op het Aantal Hoekpunten

Het aantal hoekpunten van een prisma wordt volledig bepaald door de vorm van de basis. Als de basis een driehoek is, spreken we van een driehoekig prisma. Als de basis een vierkant is, spreken we van een vierkant prisma (of een balk). En zo verder. Elke hoek van de basisfiguur wordt een hoekpunt van het prisma, en omdat er twee identieke basissen zijn, verdubbelt het aantal hoeken van de basis.

Formule voor het Aantal Hoekpunten

We kunnen een eenvoudige formule gebruiken om het aantal hoekpunten te berekenen:

Aantal hoekpunten = 2 * (Aantal zijden van de basis)

Laten we dit toepassen op verschillende soorten prisma's:

• Driehoekig Prisma: De basis is een driehoek (3 zijden). Dus, 2 * 3 = 6 hoekpunten.
• Vierkant Prisma: De basis is een vierkant (4 zijden). Dus, 2 * 4 = 8 hoekpunten.
• Vijfhoekig Prisma: De basis is een vijfhoek (5 zijden). Dus, 2 * 5 = 10 hoekpunten.
• Zeshoekig Prisma: De basis is een zeshoek (6 zijden). Dus, 2 * 6 = 12 hoekpunten.

Zoals je kunt zien, neemt het aantal hoekpunten toe naarmate het aantal zijden van de basis toeneemt. Het is cruciaal om te herkennen dat deze formule alleen van toepassing is op rechte prisma's, waarbij de zijvlakken loodrecht op de basissen staan. Voor schuine prisma's blijft het aantal hoekpunten hetzelfde, maar de geometrische eigenschappen kunnen iets complexer zijn.

Rechte Prisma's vs. Schuine Prisma's

Het is belangrijk om het verschil tussen rechte en schuine prisma's te begrijpen. Bij een recht prisma staan de zijvlakken loodrecht op de basissen. Dit betekent dat de zijvlakken rechthoeken zijn. Bij een schuin prisma staan de zijvlakken niet loodrecht op de basissen. Dit betekent dat de zijvlakken parallellogrammen zijn.

Hoewel de vorm van de zijvlakken verandert, heeft dit geen invloed op het aantal hoekpunten. Of een prisma nu recht of schuin is, het aantal hoekpunten wordt nog steeds bepaald door de vorm van de basis en de formule blijft geldig. Het is de positie van de hoekpunten die verandert, wat resulteert in een visueel "scheef" uiterlijk.

Voorbeelden uit de Praktijk

Prisma's komen in vele vormen voor in de wereld om ons heen:

• Verpakkingen: Veel dozen en verpakkingen hebben de vorm van een prisma. Denk aan een doos melk (vierkant prisma) of een chocoladeverpakking met een driehoekige vorm.
• Architectuur: Gebouwen kunnen prismatische vormen aannemen. Een flatgebouw met een rechthoekige basis is bijvoorbeeld een vierkant prisma.
• Optica: Optische prisma's worden gebruikt om licht te breken en te splitsen. Deze zijn vaak driehoekig.
• Tent: Sommige tenten, vooral die gebruikt worden voor kamperen, hebben de vorm van een driehoekig prisma.

Denk aan een Toblerone-verpakking. Dit is een driehoekig prisma. Het heeft twee driehoekige basissen en drie rechthoekige zijvlakken. Volgens onze formule heeft het 2 * 3 = 6 hoekpunten. Bekijk het de volgende keer dat je er een ziet!

Data en Prisma's

In de data visualisatie worden prisma's, of prismatische vormen, minder direct gebruikt dan andere geometrische vormen zoals balken (die speciale vierkante prisma's zijn). Echter, het concept van het begrijpen van de ruimtelijke relaties en het correct weergeven van driedimensionale data is van cruciaal belang. De principes die gelden voor het analyseren van prisma's, zoals het bepalen van volume en oppervlakte, kunnen worden toegepast op complexere datasets die ruimtelijke componenten bevatten.

Bijvoorbeeld, bij het modelleren van een stad in 3D, kunnen gebouwen worden benaderd als prisma's. Het begrijpen van de hoekpunten en de relaties daartussen is essentieel voor het correct weergeven en analyseren van de data.

Conclusie

Samenvattend, het aantal hoekpunten van een prisma wordt bepaald door de vorm van de basis. De formule Aantal hoekpunten = 2 * (Aantal zijden van de basis) is een betrouwbare manier om het aantal hoekpunten te berekenen, ongeacht of het prisma recht of schuin is. Het is belangrijk om de definities en concepten te begrijpen om de eigenschappen van verschillende prisma's te kunnen identificeren en analyseren.

Dus, de volgende keer dat je een prisma tegenkomt, onthoud dan deze eenvoudige formule en je kunt direct het aantal hoekpunten bepalen. Blijf nieuwsgierig en onderzoek de wondere wereld van de geometrie! Blijf leren!