Hoeveel Ribben Heeft Een Bol

Heb je je ooit afgevraagd hoeveel ribben een bol heeft? Het lijkt misschien een vreemde vraag. Immers, als je aan ribben denkt, denk je waarschijnlijk aan het menselijk skelet of misschien aan de ribben van een boot. Maar in de wiskunde, en dan specifiek in de topologie en meetkunde, kan het woord "ribbe" een heel andere betekenis hebben. Dit artikel duikt diep in de vraag hoeveel ribben een bol heeft, waarbij we de wiskundige concepten verkennen die nodig zijn om deze vraag te beantwoorden. We richten ons op een breed publiek, van studenten die geïnteresseerd zijn in wiskunde tot gewoon nieuwsgierige geesten.

Wat is een Ribbe Eigenlijk?

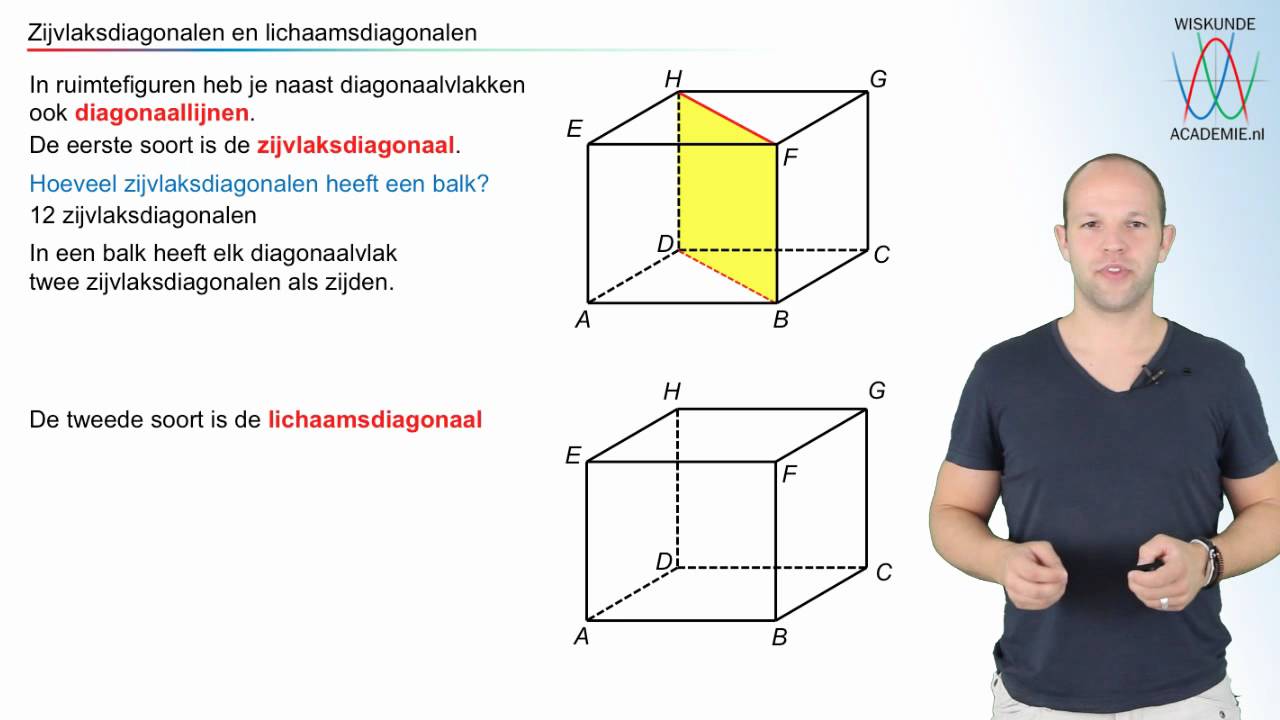
Om te begrijpen hoeveel ribben een bol heeft, moeten we eerst definiëren wat een ribbe is. In de dagelijkse taal verwijst een ribbe naar een botstructuur die bescherming biedt aan de interne organen, zoals onze borstkas. In de meetkunde en topologie daarentegen, is een ribbe een lijnsegment dat twee hoekpunten (of punten) verbindt in een graaf, een polygoon of een polyëder. Het is een element van de "rand" van een object. Denk bijvoorbeeld aan een kubus: deze heeft 12 ribben, die elk twee hoekpunten verbinden en een zijde vormen.

In de context van grafen is een ribbe eenvoudigweg een verbinding tussen twee knooppunten. Een graaf is een wiskundige structuur die bestaat uit knooppunten (of vertices) en ribben (of edges) die deze knooppunten verbinden. Grafen worden gebruikt om relaties tussen objecten te modelleren in diverse velden, zoals computerwetenschappen, sociale netwerken en biologie.

De Bol: Een Fundamenteel Geometrisch Object

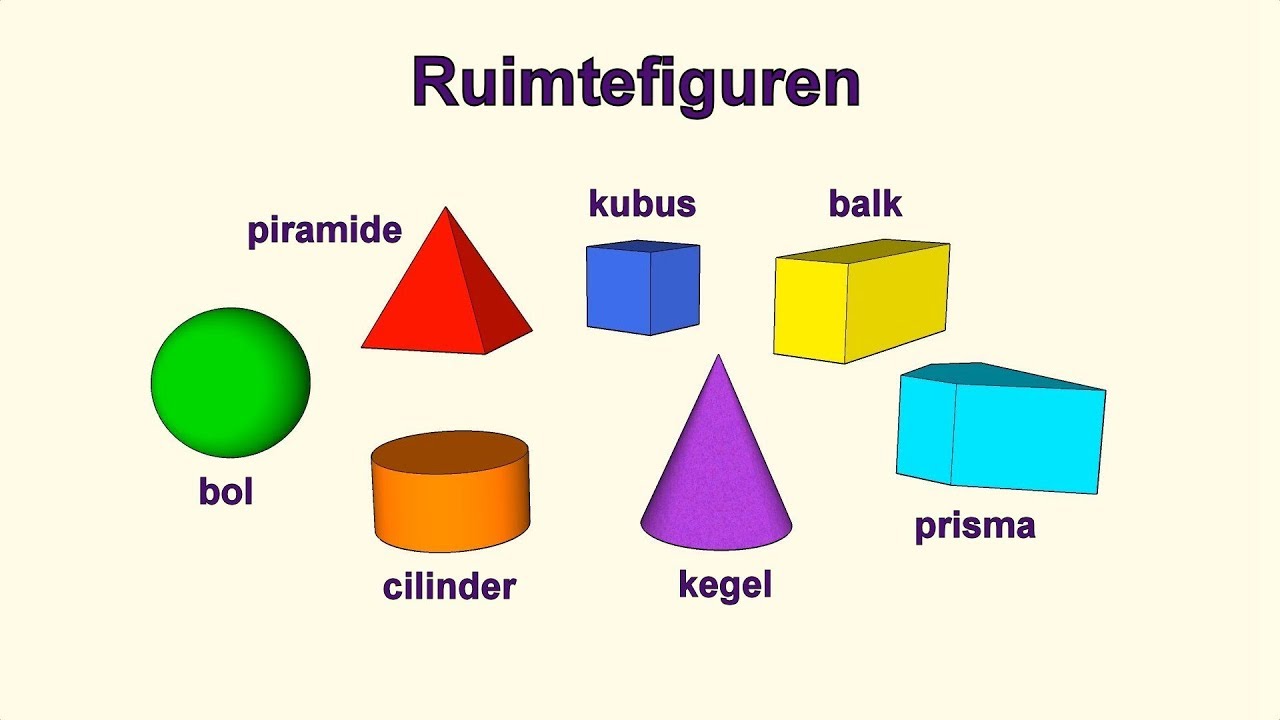
De bol is een perfect rond, driedimensionaal object. Je kunt het zien als de verzameling van alle punten die zich op een gelijke afstand (de straal) van een centraal punt bevinden. Denk aan een voetbal, een knikker, of de aarde (bij benadering). In de wiskunde is de bol een van de meest fundamentele geometrische objecten en speelt een cruciale rol in vele gebieden, waaronder differentiaalmeetkunde, topologie en fysica.

Het oppervlak van een bol heeft een aantal unieke eigenschappen. Het is bijvoorbeeld een gesloten oppervlak, wat betekent dat het geen randen heeft. Het is ook een compact en samenhangend oppervlak. Deze eigenschappen maken de bol een interessant object om te bestuderen vanuit wiskundig oogpunt.

Ribben en de Bol: Een Moeilijke Vraag

Nu komt het lastige gedeelte: hoeveel ribben heeft een bol? Direct gezien lijkt het antwoord nul. Een bol heeft geen hoekpunten en geen duidelijke rechte lijnen die ze verbinden, zoals bij een kubus of een piramide. Het is een glad, continu oppervlak.

Echter, de vraag is interessanter dan het lijkt. We kunnen de bol *benaderen* met behulp van andere geometrische vormen die wel ribben hebben. Stel je voor dat je een bol steeds beter wilt benaderen met een polyëder (een ruimtelijke figuur met platte vlakken). Hoe meer vlakken en ribben je gebruikt, hoe meer de polyëder op een bol zal lijken.

Benaderingen van de Bol

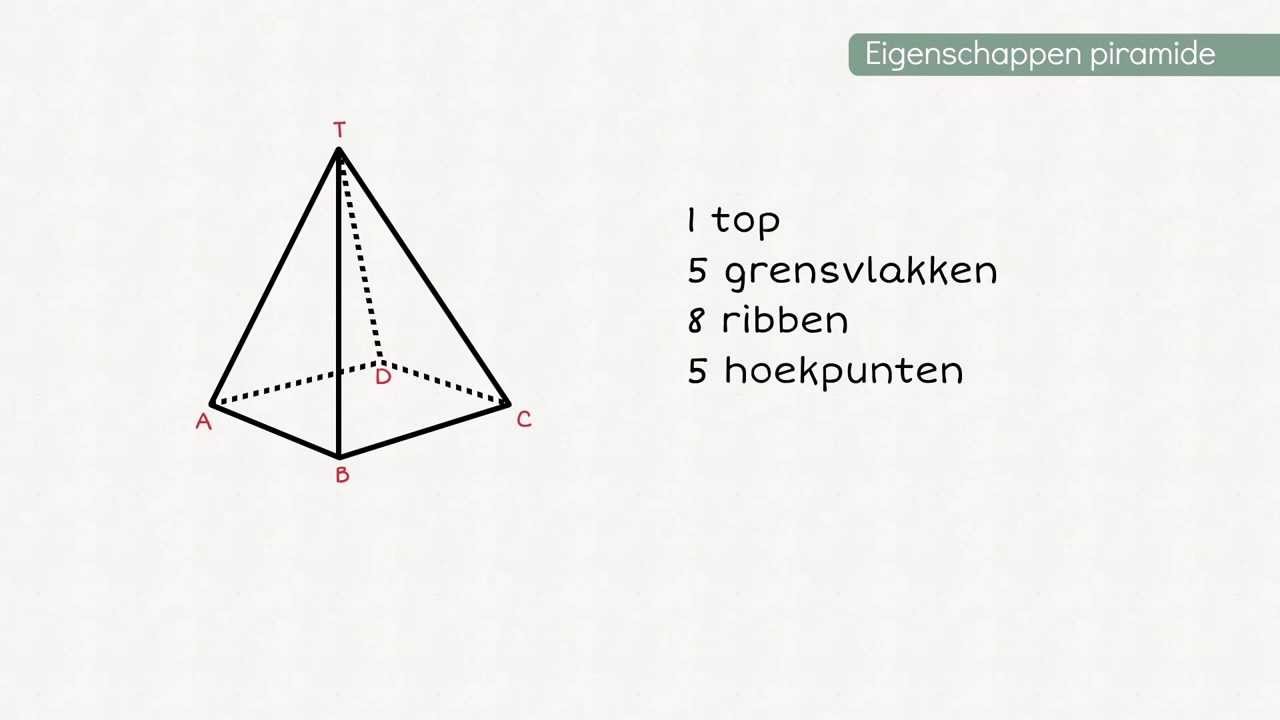
• Tetraëder: Een tetraëder is een piramide met een driehoekige basis. Het heeft 4 vlakken, 4 hoekpunten en 6 ribben. Een tetraëder is een zeer grove benadering van een bol.
• Octaëder: Een octaëder heeft 8 vlakken (driehoeken), 6 hoekpunten en 12 ribben. Het is een betere benadering dan de tetraëder.
• Icosaëder: Een icosaëder heeft 20 vlakken (driehoeken), 12 hoekpunten en 30 ribben. Het is een nog betere benadering van een bol.

Naarmate we steeds meer vlakken toevoegen aan de polyëder, komt de vorm steeds dichter bij de bol te liggen. In de limiet, als het aantal vlakken oneindig groot wordt en de grootte van elk vlak oneindig klein, *benadert* de polyëder de bol perfect. Maar zelfs in deze limiet heeft de *echte* bol nog steeds geen ribben in de klassieke meetkundige zin.

Topologie: Een Ander Perspectief

De topologie, ook wel "rubberen blad meetkunde" genoemd, is een tak van de wiskunde die zich bezighoudt met de eigenschappen van objecten die behouden blijven onder continue vervormingen. Met andere woorden, topologie is geïnteresseerd in eigenschappen die niet veranderen als je een object uitrekt, buigt, verdraait of samentrekt (zonder te scheuren of te plakken).

Vanuit topologisch oogpunt is een bol equivalent aan een kubus of een tetraëder. Dat wil zeggen, je kunt een kubus continu vervormen tot een bol zonder te scheuren of te plakken. Dit klinkt misschien contra-intuïtief, omdat een kubus duidelijk hoekpunten en ribben heeft, terwijl een bol dat niet heeft. Maar in de topologie zijn we alleen geïnteresseerd in de *connectiviteit* van de objecten, niet in hun precieze vorm of metrische eigenschappen.

Deze topologische equivalentie kan ons helpen om een andere manier te vinden om naar de ribben van een bol te kijken. Omdat een bol topologisch equivalent is aan een kubus, kunnen we stellen dat de bol in zekere zin *lijkt* op een kubus. We kunnen dus proberen om de ribben van de kubus op de bol af te beelden.

Stel je voor dat je een kubus opblaast tot een bol. De hoekpunten van de kubus worden punten op de bol, en de ribben van de kubus worden krommen op de bol. Deze krommen verbinden de punten die overeenkomen met de hoekpunten van de kubus. In deze context kunnen we zeggen dat de bol effectief 12 "ribben" heeft, overeenkomend met de ribben van de kubus na vervorming.

Euler-karakteristiek

De Euler-karakteristiek is een topologische invariant die een relatie legt tussen het aantal hoekpunten (V), ribben (E) en vlakken (F) van een polyëder. De formule is: V - E + F = 2. Voor een bol geldt, in zekere zin, dat V=2 (denk aan een Noordpool en een Zuidpool) en F=0 (er zijn geen vlakke vlakken). Om aan de Euler-formule te voldoen, zou E=0 moeten zijn, tenzij we een specifieke triangulatie van de bol kiezen, zoals hierboven besproken.

Praktische Toepassingen en Visualisaties

Hoewel de vraag naar het aantal ribben van een bol misschien abstract lijkt, heeft het wel degelijk praktische toepassingen en kan het gevisualiseerd worden in diverse contexten:

• Geodesische koepels: Architectuur van koepels gebaseerd op de geodeet, waardoor het gewicht gelijkmatig wordt verdeeld. Deze structuren benaderen een bol en zijn opgebouwd uit driehoeken die ribben vormen. De berekening van deze ribben en hun onderlinge verbindingen is essentieel voor de stabiliteit van de constructie.
• Computer graphics: Om een bol weer te geven in een computerprogramma, wordt deze vaak gemodelleerd als een polygonale mesh, een netwerk van polygonen die de bol benaderen. Elke polygoon heeft randen, die ribben zijn in de wiskundige zin.
• Wereldkaarten: Projecties van de bolvormige aarde op een plat vlak vereisen een zekere vervorming. Een veelgebruikte projectie is de Mercatorprojectie, die de aarde verdeelt in een rooster van lijnen (meridianen en parallellen). Deze lijnen kunnen worden gezien als een soort ribben op de bol, die helpen bij het navigeren en lokaliseren van plaatsen.
• Moleculaire structuren: Sommige moleculen, zoals fullerenen (bijvoorbeeld buckminsterfullereen, C60), hebben een bolvormige structuur. De bindingen tussen de atomen kunnen worden gezien als de ribben van een bolvormig netwerk.

Conclusie

Dus, hoeveel ribben heeft een bol? Het korte antwoord is: geen, in de traditionele meetkundige zin. Een bol is een glad oppervlak zonder hoekpunten of rechte lijnen die ze verbinden. Echter, als we de bol benaderen met polygonen, topologische equivalenties overwegen, of practicale toepassingen in acht nemen, dan kunnen we op verschillende manieren een *concept* van ribben op een bol construeren.

De vraag is niet zozeer wat het *correcte* antwoord is, maar eerder wat de verschillende perspectieven en benaderingen ons leren over de aard van wiskundige objecten en hun relatie tot de werkelijkheid. De wiskunde is een gereedschap om de wereld om ons heen te begrijpen, en soms leidt het stellen van ogenschijnlijk eenvoudige vragen tot diepere inzichten in complexe concepten.

Hopelijk heeft dit artikel je geholpen om de vraag "hoeveel ribben heeft een bol?" op een nieuwe manier te benaderen. Blijf nieuwsgierig, blijf vragen stellen, en blijf de wonderen van de wiskunde ontdekken!

Het belangrijkste is de reis, niet de bestemming. En in dit geval, was de reis een interessante verkenning van geometrie, topologie en abstract denken!