Hoeveel Vlakken Heeft Een Piramide

Weet je nog dat je als kind speelde met bouwstenen? Misschien heb je wel eens geprobeerd om een piramide te bouwen. Het is fascinerend hoe zo'n eenvoudige vorm al eeuwenlang tot de verbeelding spreekt. Maar heb je er ooit echt bij stilgestaan hoeveel vlakken een piramide eigenlijk heeft? Het antwoord is niet zo simpel als je misschien denkt, want het hangt af van het type piramide.

In dit artikel duiken we in de wereld van piramides en ontdekken we hoe je het aantal vlakken kunt bepalen. We leggen het uit in begrijpelijke taal, zonder ingewikkelde wiskundige formules. En we laten je zien waarom dit meer is dan alleen een schoolsommen: de vorm van piramides is van invloed op architectuur, design en zelfs onze manier van denken over stabiliteit en hiërarchie.

De Basis: Wat is een Piramide?

Laten we beginnen met de basis. Een piramide is een ruimtelijke figuur met een veelhoek als basis en driehoekige zijvlakken die samenkomen in een punt, de top. De basis kan een driehoek, vierkant, vijfhoek of zelfs een nog complexere veelhoek zijn. Elk van deze mogelijkheden leidt tot een ander type piramide, en dus ook tot een ander aantal vlakken.

Denk bijvoorbeeld aan de piramides van Gizeh in Egypte. Die hebben een vierkante basis. Maar je kunt je ook een piramide voorstellen met een driehoekige basis, een tetraëder. Het is belangrijk om dat in je achterhoofd te houden.

Hoeveel Vlakken Heeft een Piramide met een Vierkante Basis?

Dit is waarschijnlijk het type piramide waar de meeste mensen aan denken. De piramide met een vierkante basis is een klassieker. Hoeveel vlakken heeft zo'n piramide nu precies?

• De basis: Dit is het vierkante vlak aan de onderkant.
• De zijvlakken: Er zijn vier driehoekige zijvlakken die vanuit elke zijde van het vierkant omhoog lopen naar de top.

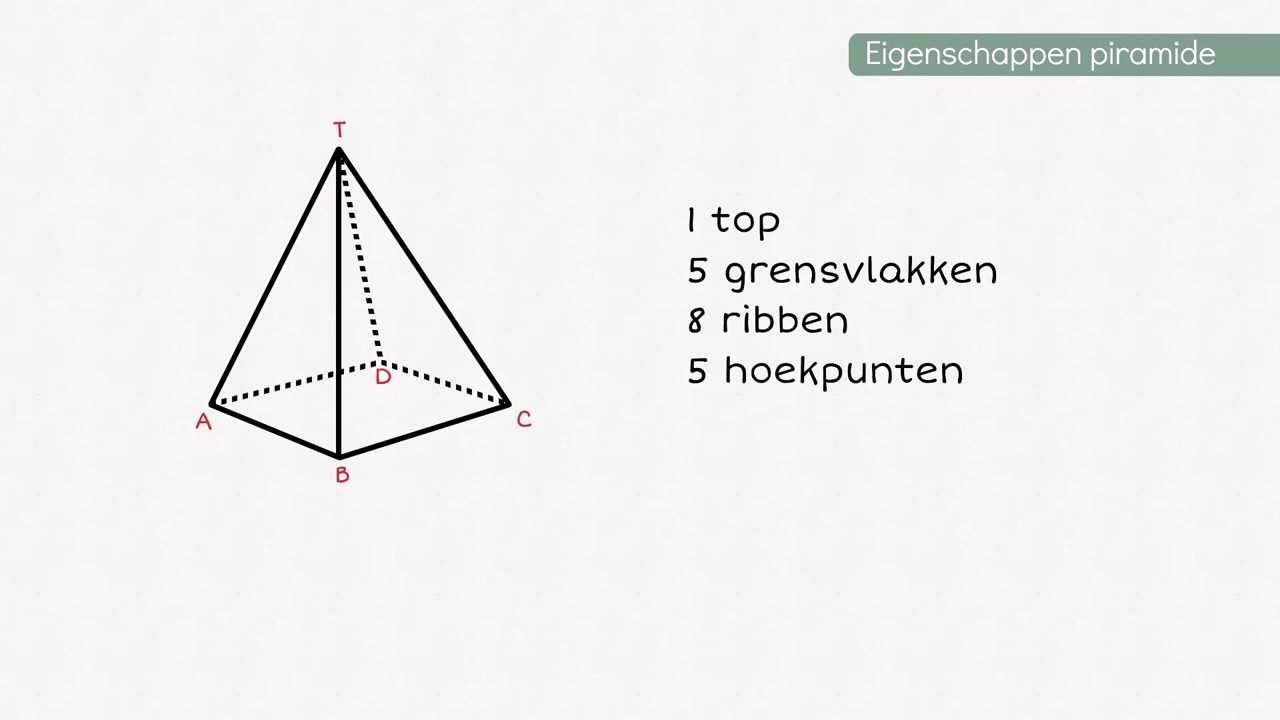
Dus, in totaal heeft een piramide met een vierkante basis vijf vlakken (1 vierkant + 4 driehoeken). Simpel, toch?

En Hoe Zit het met Andere Basissen?

De uitdaging begint pas echt wanneer we kijken naar piramides met andere vormen als basis. Hier is een overzicht:

Piramide met een Driehoekige Basis (Tetraëder)

Een piramide met een driehoekige basis wordt ook wel een tetraëder genoemd. In dit geval is elk vlak een driehoek. Het heeft dus vier vlakken. Een tetraëder is bijzonder omdat elk vlak als basis kan dienen.

Piramide met een Vijfhoekige Basis

Een piramide met een vijfhoekige basis heeft een vijfhoek aan de onderkant en vijf driehoekige zijvlakken. Dat betekent dat er in totaal zes vlakken zijn (1 vijfhoek + 5 driehoeken).

Piramide met een Zeshoekige Basis

Je raadt het al: een piramide met een zeshoekige basis heeft een zeshoek als basis en zes driehoekige zijvlakken. Dat maakt in totaal zeven vlakken (1 zeshoek + 6 driehoeken).

De Algemene Regel

Kun je al een patroon ontdekken? Er is een eenvoudige regel die je kunt toepassen om het aantal vlakken van een piramide te bepalen:

Aantal vlakken = Aantal zijden van de basis + 1

Dus, als je een piramide hebt met een basis die 10 zijden heeft (een decagoon), dan heeft de piramide 10 + 1 = 11 vlakken.

Waarom is dit Belangrijk?

Je vraagt je misschien af: "Waarom moet ik dit eigenlijk weten?" Het antwoord is dat het begrijpen van geometrische vormen en hun eigenschappen cruciaal is in veel verschillende gebieden:

• Architectuur: Architecten gebruiken kennis van geometrie om structuren te ontwerpen die stabiel en esthetisch aantrekkelijk zijn. De vorm van een piramide biedt bijvoorbeeld een natuurlijke stabiliteit.
• Engineering: Ingenieurs gebruiken geometrie om bruggen, gebouwen en andere constructies te ontwerpen.
• Design: Designers gebruiken geometrie om producten te ontwerpen die functioneel en mooi zijn. Denk aan de vorm van een verpakking, een meubelstuk of zelfs een logo.
• Wiskunde en Wetenschap: Het begrijpen van ruimtelijke figuren is essentieel voor wiskundig redeneren en het oplossen van wetenschappelijke problemen.

Bovendien is het stimulerend om je ruimtelijk inzicht te ontwikkelen. Het helpt je om de wereld om je heen beter te begrijpen en problemen op een creatieve manier op te lossen. Het draagt ook bij aan een logische manier van denken.

Veelvoorkomende Misvattingen

Een veelvoorkomende misvatting is dat alle piramides vierkant zijn. Zoals we hebben gezien, kunnen piramides verschillende vormen als basis hebben. Het is belangrijk om te onthouden dat de vorm van de basis bepaalt hoeveel vlakken de piramide heeft.

Een andere misvatting is dat het aantal hoekpunten hetzelfde is als het aantal vlakken. Dit is niet waar. Een piramide met een vierkante basis heeft 5 vlakken, maar 5 hoekpunten (de 4 hoeken van het vierkant + de top).

Counterpoint: Is dit Echt Relevante Kennis?

Sommigen beweren misschien dat het tellen van vlakken van een piramide een nutteloze bezigheid is, iets dat alleen relevant is voor wiskundeleraren of architectuurstudenten. En ja, in het dagelijks leven zul je waarschijnlijk niet vaak gevraagd worden om het aantal vlakken van een piramide te berekenen.

Echter, de vaardigheden die je ontwikkelt door met geometrische vormen te werken – ruimtelijk inzicht, probleemoplossend vermogen, logisch redeneren – zijn wel degelijk waardevol in veel verschillende contexten. Of je nu een kast in elkaar zet, een routebeschrijving volgt, of een complex probleem op je werk aanpakt, deze vaardigheden komen van pas.

Oplossingen en Toepassingen

Laten we eens kijken naar enkele concrete toepassingen:

• Ontwerp van verpakkingen: Bedrijven gebruiken kennis van geometrie om verpakkingen te ontwerpen die efficiënt, aantrekkelijk en beschermend zijn. Een piramidevormige verpakking kan bijvoorbeeld stabieler zijn dan een rechthoekige verpakking.
• Architectuur: Architecten gebruiken piramidevormen om structuren te creëren die sterk en stabiel zijn. Denk aan de piramides van Gizeh, maar ook aan modernere gebouwen met piramidevormige elementen.
• Spelletjes en puzzels: Veel spelletjes en puzzels, zoals Rubik's kubus, zijn gebaseerd op geometrische principes. Het begrijpen van de vormen en hun eigenschappen kan je helpen om deze spellen te beheersen.
• Virtuele Realiteit en 3D-Modeling: Het creëren van realistische 3D-modellen vereist een grondige kennis van geometrie en ruimtelijke figuren.

Conclusie

Dus, hoeveel vlakken heeft een piramide? Het antwoord hangt af van de vorm van de basis. Een piramide met een vierkante basis heeft 5 vlakken, een piramide met een driehoekige basis (tetraëder) heeft 4 vlakken, en zo verder. De algemene regel is: aantal vlakken = aantal zijden van de basis + 1.

Het begrijpen van geometrische vormen is meer dan alleen een wiskundige oefening. Het is een waardevolle vaardigheid die je kan helpen in veel verschillende gebieden, van architectuur tot design tot probleemoplossing. Het scherpt je ruimtelijk inzicht aan en helpt je om de wereld om je heen beter te begrijpen.

En nu jij: welke geometrische vorm fascineert jou het meest en waarom?