How Do You Find Inflection Points

Het vinden van inflectiepunten, ook wel buigpunten genoemd, is een cruciale vaardigheid in de calculus en heeft wijdverspreide toepassingen in diverse vakgebieden. Een inflectiepunt markeert een verandering in de concaviteit van een functie; het is het punt waar een curve overgaat van hol naar bol, of omgekeerd. Het begrijpen en identificeren van inflectiepunten kan waardevolle inzichten verschaffen in het gedrag en de trends van functies, wat van onschatbare waarde is bij het modelleren en analyseren van reële wereldscenario's.

Wat zijn Inflectiepunten en Waarom Zijn Ze Belangrijk?

In essentie is een inflectiepunt het punt op een curve waar de concaviteit verandert. Concaviteit verwijst naar de richting waarin een curve 'buigt'. Een curve is concaaf naar boven (of hol) als deze eruitziet als een lachend gezicht, en concaaf naar beneden (of bol) als deze eruitziet als een fronsend gezicht. Het inflectiepunt is het specifieke punt waar de curve switcht tussen deze twee staten. Het is belangrijk op te merken dat een functie continu en differentieerbaar moet zijn in de omgeving van een inflectiepunt.

Het belang van inflectiepunten ligt in hun vermogen om kritieke veranderingen in het gedrag van een functie aan te duiden. Denk bijvoorbeeld aan een grafiek die de groei van een bedrijf weergeeft. Een inflectiepunt zou kunnen aangeven wanneer de groei versnelt of vertraagt. Of in de natuurkunde, een inflectiepunt in een grafiek die de positie van een object weergeeft, zou een verandering in de richting van de versnelling kunnen aanduiden. Zonder deze punten zouden we cruciale informatie over het gedrag van de functie missen.

De Relatie met de Tweede Afgeleide

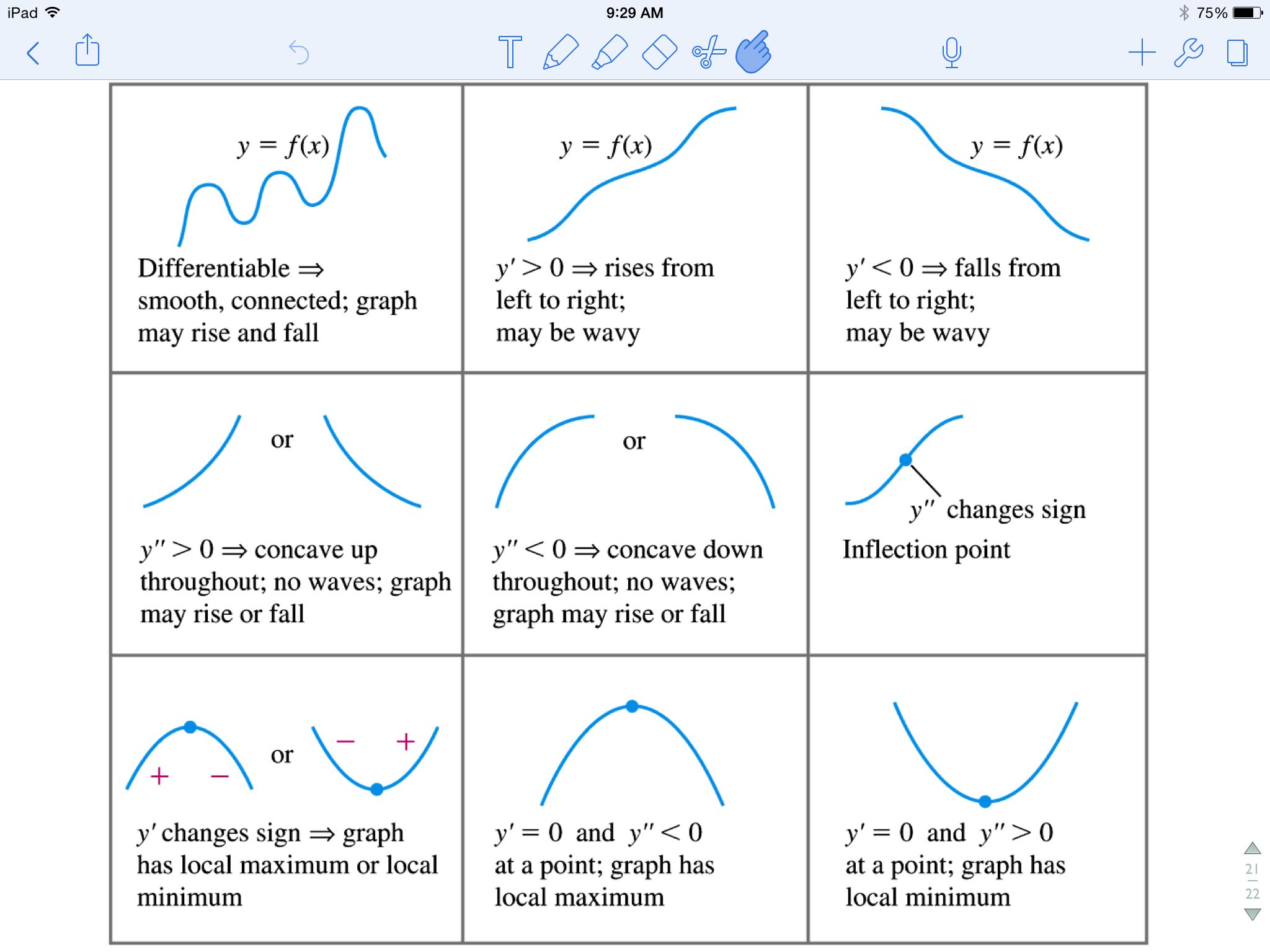
De sleutel tot het vinden van inflectiepunten ligt in de tweede afgeleide van de functie. De tweede afgeleide, aangeduid als f''(x), geeft de snelheid van verandering van de helling (de eerste afgeleide) van de functie weer. Met andere woorden, de tweede afgeleide vertelt ons over de concaviteit van de functie. Wanneer f''(x) > 0, is de functie concaaf naar boven. Wanneer f''(x) < 0, is de functie concaaf naar beneden. Op het inflectiepunt zal de tweede afgeleide ofwel gelijk zijn aan nul, of niet bestaan.

Hoe Vind je Inflectiepunten: Een Stapsgewijze Handleiding

Het vinden van inflectiepunten volgt een relatief eenvoudig proces. Hieronder volgt een stapsgewijze handleiding:

1. Bereken de Tweede Afgeleide: Dit is de eerste en meest cruciale stap. Bepaal de tweede afgeleide van de functie, f''(x). Je moet eerst de eerste afgeleide, f'(x), berekenen en deze vervolgens nogmaals differentiëren.
2. Vind Mogelijke Inflectiepunten: Zoek de waarden van x waarvoor f''(x) = 0 of f''(x) niet bestaat. Deze waarden worden kandidaten voor inflectiepunten genoemd. Het is belangrijk om te onthouden dat niet alle punten waar f''(x) = 0 inflectiepunten zijn.
3. Test de Concaviteit: Om te bepalen of een kandidaat daadwerkelijk een inflectiepunt is, moeten we de concaviteit van de functie aan weerszijden van het punt testen. Dit kan worden gedaan door testwaarden te kiezen die kleiner en groter zijn dan de kandidaat-waarde van x en deze in f''(x) te pluggen.
4. Analyseer de Resultaten: Als de tweede afgeleide van teken verandert (bijvoorbeeld van positief naar negatief of van negatief naar positief) bij de kandidaat-waarde van x, dan is dat punt een inflectiepunt. Als het teken niet verandert, dan is het geen inflectiepunt.
5. Bepaal de y-coördinaat: Om het volledige inflectiepunt (x, y) te vinden, substitueer je de x-waarde van het inflectiepunt terug in de originele functie, f(x), om de bijbehorende y-waarde te vinden.

Voorbeelden en Toepassingen

Laten we een paar voorbeelden bekijken om het proces te illustreren:

Voorbeeld 1: Een Simpele Polynoomfunctie

Beschouw de functie f(x) = x³ - 6x² + 5x - 2.

1. Eerste afgeleide: f'(x) = 3x² - 12x + 5
2. Tweede afgeleide: f''(x) = 6x - 12
3. Mogelijke inflectiepunten: Stel f''(x) = 0, dus 6x - 12 = 0. Dit geeft x = 2.
4. Test de concaviteit:
   • Kies x = 1 (kleiner dan 2): f''(1) = 6(1) - 12 = -6 (concaaf naar beneden)
   • Kies x = 3 (groter dan 2): f''(3) = 6(3) - 12 = 6 (concaaf naar boven)
   Aangezien de concaviteit verandert, is x = 2 een inflectiepunt.
5. Bepaal de y-coördinaat: f(2) = (2)³ - 6(2)² + 5(2) - 2 = 8 - 24 + 10 - 2 = -8. Het inflectiepunt is (2, -8).

Voorbeeld 2: Economische Data - Groeicurves

Stel dat we de groei van de omzet van een bedrijf over een bepaalde periode analyseren. De omzet kan worden gemodelleerd door een functie. Een inflectiepunt op deze functie zou een belangrijke verandering in de groeisnelheid aangeven. Bijvoorbeeld, een farmaceutisch bedrijf dat een nieuw medicijn lanceert, zou mogelijk een inflectiepunt zien in de verkoopcijfers, wanneer de initiële snelle groei afneemt, en de verkoop stabiliseert.

Voorbeeld 3: COVID-19 Verspreiding (vereenvoudigd model)

Hoewel de werkelijke COVID-19-modellering complex is, kunnen we een vereenvoudigd model gebruiken om het concept van inflectiepunten te illustreren. Stel je een grafiek voor die het cumulatieve aantal COVID-19-gevallen in de loop van de tijd weergeeft. Aanvankelijk zien we een exponentiële groei (concaaf naar boven). Naarmate maatregelen zoals lockdowns en vaccinaties worden ingevoerd, kan de verspreiding vertragen. Het punt waar de curve overgaat van exponentiële groei naar afnemende groei is een inflectiepunt. Dit zou belangrijke informatie geven over de effectiviteit van de maatregelen om de verspreiding van het virus te beheersen.

Waarom de Concaviteit Test Cruciaal is

Het is belangrijk om te benadrukken dat niet elk punt waar de tweede afgeleide nul is, een inflectiepunt is. De concaviteit moet daadwerkelijk veranderen op dat punt. Beschouw bijvoorbeeld de functie f(x) = x⁴. De tweede afgeleide is f''(x) = 12x². Als we f''(x) = 0 stellen, vinden we x = 0. Echter, f''(x) is altijd positief of nul (namelijk bij x=0), dus de concaviteit verandert niet. Daarom is x = 0 geen inflectiepunt voor deze functie.

Conclusie en Call to Action

Het vinden van inflectiepunten is een waardevolle vaardigheid met toepassingen in diverse disciplines. Door de stapsgewijze handleiding te volgen, kan men deze punten succesvol identificeren en analyseren om diepere inzichten te verkrijgen in het gedrag van functies. Het is belangrijk om de relatie tussen de tweede afgeleide en concaviteit te begrijpen, en om de concaviteit te testen om te bevestigen dat een kandidaat daadwerkelijk een inflectiepunt is.

Oefen met verschillende functies en real-world voorbeelden om je begrip en vaardigheden te verbeteren. Probeer complexe functies te analyseren, modellen van economische groei of andere data, en probeer de inflectiepunten te vinden. Experimenteer met verschillende tools zoals grafische rekenmachines of software voor wiskundige berekeningen om het proces te visualiseren en te vereenvoudigen. Het beheersen van deze techniek zal je analytische vaardigheden aanzienlijk verbeteren en je vermogen om waardevolle conclusies te trekken uit data.