Levene's Test For Equality Of Variance

Laten we eerlijk zijn, statistiek kan soms voelen als een doolhof. Je bent bezig met een onderzoek, hebt data verzameld, en wilt nu écht interessante conclusies trekken. Maar dan duiken er allerlei tests en aannames op waar je je zorgen over moet maken. De Levene's test voor gelijkheid van varianties is zo'n test die vaak over het hoofd wordt gezien, maar cruciaal kan zijn voor de betrouwbaarheid van je resultaten. Vooral als je werkt met statistische methoden zoals de t-test of ANOVA.

Waarom is dit belangrijk? Omdat het negeren van de aannames achter deze tests kan leiden tot verkeerde conclusies. En dat willen we natuurlijk voorkomen. Dus laten we eens kijken wat Levene's test precies doet, waarom het belangrijk is, en hoe je het kunt gebruiken.

Waarom gelijkheid van varianties ertoe doet

Stel je voor: je vergelijkt de prestaties van twee verschillende groepen leerlingen op een wiskunde-examen. Je wilt weten of er een significant verschil is tussen de twee groepen. Om dit te doen, zou je misschien een t-test gebruiken. Maar die test heeft een belangrijke aanname: de varianties (de spreiding van de scores) van de twee groepen moeten ongeveer gelijk zijn.

Wat gebeurt er als die varianties niet gelijk zijn? Dan kan je t-test onterecht een significant verschil vinden, of juist een verschil missen dat er wel is. Dit staat bekend als een Type I of Type II fout. Met andere woorden, je trekt een verkeerde conclusie, wat kan leiden tot verkeerde beslissingen en interpretaties.

Levene's test helpt je om te controleren of aan deze aanname van gelijkheid van varianties is voldaan. Het is een soort "vooronderzoek" voordat je verder gaat met de t-test of ANOVA.

Wat is Levene's test?

Levene's test is een statistische test die de nulhypothese onderzoekt dat de varianties van twee of meer groepen gelijk zijn. De nulhypothese is dus dat er géén verschil is in de varianties.

De test werkt door de absolute afwijkingen van elke data-punt ten opzichte van het gemiddelde (of de mediaan) van de groep te berekenen. Vervolgens voert de test een ANOVA uit op deze absolute afwijkingen. Als de ANOVA significant is, betekent dit dat er een significant verschil is in de spreiding (variantie) tussen de groepen.

Simpel gezegd: Levene's test kijkt niet naar de data zelf, maar naar hoe ver elk data-punt afwijkt van het centrum van zijn eigen groep. Grote verschillen in deze afwijkingen suggereren verschillende varianties.

Hoe werkt het in de praktijk?

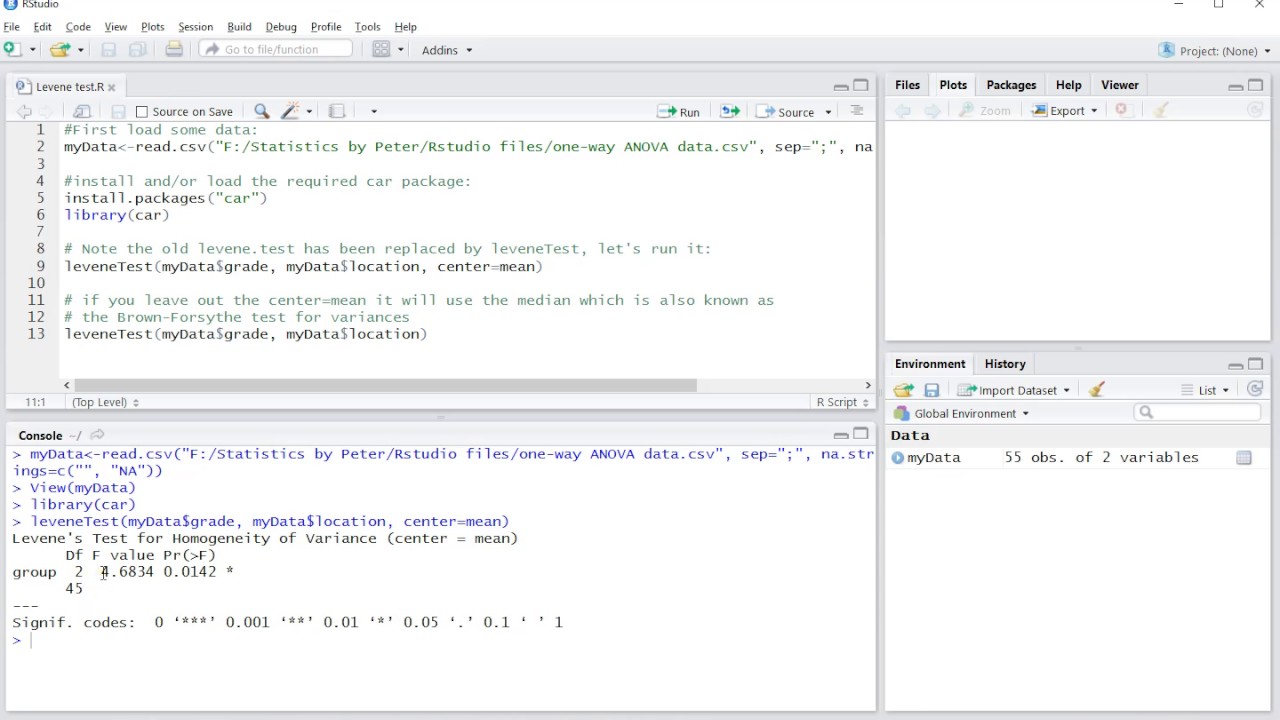
Je voert Levene's test meestal uit met behulp van statistische software zoals SPSS, R, of Python. De software berekent de teststatistiek (meestal een F-waarde) en de bijbehorende p-waarde.

• P-waarde > α (significantieniveau): Je verwerpt de nulhypothese niet. Dit betekent dat er geen significant bewijs is dat de varianties verschillen. Je kunt doorgaan met je t-test of ANOVA.
• P-waarde ≤ α (significantieniveau): Je verwerpt de nulhypothese. Dit betekent dat er een significant verschil is in de varianties. Je moet alternatieve methoden overwegen (zie hieronder).

Het significantieniveau (α) is meestal 0.05, maar dit kan variëren afhankelijk van het onderzoeksgebied en de mate van zekerheid die je wilt hebben.

Alternatieven wanneer de varianties niet gelijk zijn

Wat doe je als Levene's test aantoont dat de varianties niet gelijk zijn? Geen paniek! Er zijn verschillende opties:

• Welch's t-test: Dit is een variant van de t-test die geen aanname van gelijke varianties maakt. Het is een robuust alternatief dat je kunt gebruiken als Levene's test significant is.
• Brown-Forsythe test: Een andere test voor gelijkheid van varianties die robuuster is dan Levene's test, vooral wanneer de data niet normaal verdeeld is.
• Non-parametrische tests: Tests zoals de Mann-Whitney U test (voor het vergelijken van twee groepen) of de Kruskal-Wallis test (voor het vergelijken van meer dan twee groepen) maken geen aannames over de verdeling van de data of de gelijkheid van varianties.
• Data transformaties: Soms kun je de data transformeren (bijvoorbeeld met een logaritmische transformatie) om de varianties meer gelijk te maken. Echter, dit is niet altijd de beste oplossing, omdat het de interpretatie van de resultaten kan bemoeilijken.

De keuze voor de beste alternatieve methode hangt af van de specifieke data en de onderzoeksvraag. Het is belangrijk om de voor- en nadelen van elke methode zorgvuldig te overwegen.

Kritiek en nuances

Hoewel Levene's test nuttig is, is het belangrijk om ook de beperkingen te kennen:

• Gevoeligheid voor niet-normaliteit: Levene's test is zelf gevoelig voor afwijkingen van de normaliteit. Als de data niet normaal verdeeld is, kan de test onterecht een significant verschil in varianties detecteren.
• Steekproefgrootte: Bij grote steekproeven is Levene's test zeer krachtig en kan het kleine verschillen in varianties detecteren die in de praktijk niet relevant zijn. Bij kleine steekproeven is de test mogelijk niet gevoelig genoeg om echte verschillen te detecteren.
• Alternatieve interpretaties: Soms is een verschil in varianties op zichzelf al een interessante bevinding. Het kan bijvoorbeeld aangeven dat een bepaalde interventie meer effect heeft op sommige individuen dan op anderen.

Sommige statistici stellen dat het beter is om de aanname van gelijke varianties niet te testen, maar in plaats daarvan altijd een robuustere test zoals Welch's t-test te gebruiken. Dit vermijdt de potentiële problemen die gepaard gaan met Levene's test.

De real-world impact

Denk aan het testen van de effectiviteit van een nieuw medicijn. Stel dat je de bloeddruk meet van twee groepen patiënten: één groep krijgt het nieuwe medicijn, de andere groep een placebo. Als de variantie in de bloeddruk van de medicijngroep veel groter is dan die van de placebogroep, kan dit betekenen dat het medicijn bij sommige patiënten een sterk effect heeft, terwijl het bij anderen nauwelijks werkt. Dit is waardevolle informatie die je zou missen als je alleen naar het gemiddelde verschil keek.

In het onderwijs kan het vergelijken van de prestaties van leerlingen uit verschillende scholen met verschillende onderwijsmethoden laten zien dat een bepaalde methode de leerresultaten van sommige leerlingen verbetert, terwijl het de prestaties van andere leerlingen juist negatief beïnvloedt. Het identificeren van deze verschillen is cruciaal voor het optimaliseren van het onderwijs.

Samenvatting en conclusie

Levene's test voor gelijkheid van varianties is een belangrijk instrument in de gereedschapskist van elke statisticus. Het helpt je om de aannames achter statistische tests zoals de t-test en ANOVA te controleren, en om verkeerde conclusies te vermijden. Hoewel de test zijn beperkingen heeft, biedt het waardevolle informatie over de spreiding van je data en de potentiële verschillen tussen groepen.

Kortom:

• Levene's test controleert of de varianties van groepen gelijk zijn.
• Ongelijke varianties kunnen leiden tot onbetrouwbare resultaten van t-tests en ANOVA.
• Als Levene's test significant is, overweeg alternatieve methoden zoals Welch's t-test of non-parametrische tests.
• Houd rekening met de beperkingen van Levene's test, zoals de gevoeligheid voor niet-normaliteit en de invloed van de steekproefgrootte.

Door bewust om te gaan met de aannames achter statistische tests, kun je de betrouwbaarheid en validiteit van je onderzoek verbeteren en écht interessante conclusies trekken.

Nu je meer weet over Levene's test, hoe ga je dit toepassen in je eigen onderzoek? En welke andere statistische tests vind je uitdagend om te begrijpen?