Linear Algebra And Its Applications Answers

Herken je dat? Urenlang zwoegen op lineaire algebra, vastzitten op die ene, cruciale opgave? Je bent niet de enige. Lineaire algebra, met zijn matrices, vectoren en transformaties, kan soms aanvoelen als een ondoordringbare jungle. En wanneer je dan eindelijk denkt de oplossing te hebben, is het vaak nog een uitdaging om je antwoord te *controleren* en te verifiëren. De juiste antwoorden, correct uitgelegd, kunnen het verschil maken tussen frustratie en begrip.

Dit artikel is bedoeld als een gids, niet alleen om de antwoorden te vinden, maar ook om het *waarom* achter de antwoorden te begrijpen. We duiken in de wereld van lineaire algebra en bekijken hoe je effectief antwoorden kunt vinden en interpreteren, zodat je écht grip krijgt op de materie.

Waarom Lineaire Algebra Zo Belangrijk Is

Voordat we naar de antwoorden kijken, is het belangrijk te beseffen waarom lineaire algebra zo’n fundamenteel vak is. Het is de basis voor vele andere disciplines, waaronder machine learning, computer graphics, econometrie en natuurkunde. Denk aan het trainen van een AI-model: dat draait in essentie op lineaire algebraïsche bewerkingen. Of het renderen van een 3D-object op je scherm: matrices spelen een sleutelrol. Zonder een stevige basis in lineaire algebra, wordt het moeilijk om deze complexere onderwerpen te begrijpen en toe te passen.

"Linear algebra is arguably the most important subject in all of mathematics for students in engineering and science," aldus Gilbert Strang, een gerenommeerd wiskundige en auteur op het gebied van lineaire algebra. Deze quote onderstreept het belang van het vakgebied.

De Uitdagingen bij het Vinden van Antwoorden

Het vinden van correcte antwoorden op lineaire algebra opgaven kan om verschillende redenen lastig zijn:

• Complexiteit: De concepten zijn abstract en vereisen een diepgaand begrip.
• Formele Notatie: De notatie met matrices en vectoren kan intimiderend zijn.
• Veel Mogelijkheden: Er zijn vaak verschillende manieren om een probleem op te lossen, en het is niet altijd duidelijk welke de beste is.
• Foutgevoeligheid: Kleine fouten in de berekeningen kunnen leiden tot compleet verkeerde antwoorden.

Het is dus cruciaal om systematisch te werk te gaan en gebruik te maken van de juiste hulpmiddelen.

Strategieën voor het Vinden van Correcte Antwoorden

Hier zijn enkele effectieve strategieën om je te helpen bij het vinden en begrijpen van de juiste antwoorden in lineaire algebra:

1. Begrijp de Basisconcepten

Begin met het *begrijpen* van de basisconcepten. Zorg ervoor dat je een solide basis hebt in vectoren, matrices, lineaire transformaties, eigenwaarden en eigenvectoren. Zonder een goed begrip van deze fundamentele concepten, zul je moeite hebben met het oplossen van complexere problemen. Lees de definities aandachtig, bekijk voorbeelden en oefen met eenvoudige opgaven.

2. Gebruik een Stapsgewijze Aanpak

Breek complexe problemen op in kleinere, beter beheersbare stappen. Schrijf elke stap duidelijk op en controleer je werk zorgvuldig. "The key is to work systematically and to be meticulous in your calculations," zegt Professor David Lay in zijn bekende handboek over lineaire algebra. Deze nauwkeurigheid is cruciaal om fouten te minimaliseren.

3. Visualiseer de Problemen

Lineaire algebra leent zich goed voor visualisatie. Probeer de vectoren en transformaties in de ruimte te visualiseren. Gebruik grafische hulpmiddelen zoals GeoGebra of MATLAB om matrices en vectoren te plotten en hun effecten te visualiseren. Dit kan je helpen om een beter *intuïtief* begrip te krijgen van de problemen en de oplossingen.

4. Maak Gebruik van Beschikbare Hulpmiddelen

Er zijn tal van hulpmiddelen beschikbaar die je kunnen helpen bij het oplossen van lineaire algebra problemen:

• Handboeken: Goede handboeken bieden gedetailleerde uitleg, voorbeelden en opgaven. Kies een handboek dat past bij jouw niveau en leerstijl.
• Online Resources: Websites zoals Khan Academy, MIT OpenCourseWare en YouTube bieden gratis tutorials en video's over lineaire algebra.
• Software: Softwarepakketten zoals MATLAB, Mathematica en Python (met de NumPy-bibliotheek) kunnen je helpen bij het uitvoeren van complexe berekeningen en het visualiseren van resultaten.
• Forum en Vraagbaken: Sites zoals Stack Exchange (Mathematics) kunnen nuttig zijn voor het stellen van vragen en het vinden van antwoorden op specifieke problemen.

5. Controleer Je Antwoorden

Het is essentieel om je antwoorden te controleren. Er zijn verschillende manieren om dit te doen:

• Substitutie: Vul je antwoord in de oorspronkelijke vergelijking en kijk of het klopt.
• Alternatieve Methoden: Los het probleem op met een andere methode en vergelijk de resultaten.
• Software: Gebruik software om je antwoord te controleren. Bijvoorbeeld, gebruik MATLAB om de inverse van een matrix te berekenen en vergelijk dit met je eigen berekening.

6. Zoek Hulp wanneer Nodig

Aarzel niet om hulp te vragen als je vastzit. Praat met je docent, medestudenten of een tutor. Samenwerking kan je helpen om nieuwe perspectieven te krijgen en je begrip te verdiepen. Leg uit waar je precies vastloopt, zodat anderen je gerichter kunnen helpen.

Praktische Voorbeelden en Tips

Laten we eens kijken naar een paar praktische voorbeelden en tips:

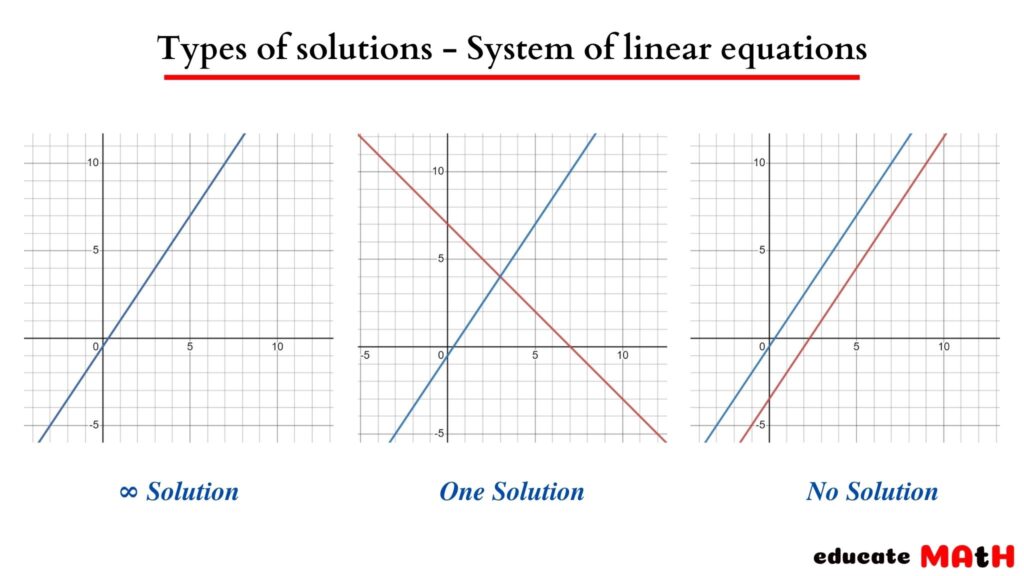
Voorbeeld 1: Het Oplossen van een Stelsel Vergelijkingen

Stel, je hebt het volgende stelsel vergelijkingen:

2x + y = 5

x - y = 1

Je kunt dit stelsel oplossen met behulp van verschillende methoden, zoals substitutie, eliminatie of matrixrekening. Met matrixrekening zet je het stelsel om in een matrixvergelijking:

[2 1][x] = [5]

[1 -1][y] [1]

Vervolgens kun je de inverse van de matrix [2 1; 1 -1] berekenen en vermenigvuldigen met de vector [5; 1] om de waarden van x en y te vinden. Het controleren van je antwoord doe je door de gevonden waarden voor x en y in de oorspronkelijke vergelijkingen te substitueren.

Voorbeeld 2: Het Berekenen van Eigenwaarden en Eigenvectoren

Het berekenen van eigenwaarden en eigenvectoren kan complex zijn. Zorg ervoor dat je de definitie van eigenwaarden en eigenvectoren begrijpt: een eigenvector v van een matrix A verandert niet van richting wanneer A erop wordt toegepast; hij wordt alleen geschaald met een factor λ (de eigenwaarde). Dit wordt weergegeven door de vergelijking Av = λv.

Gebruik software zoals MATLAB om de eigenwaarden en eigenvectoren te controleren die je met de hand hebt berekend. Dit is een snelle en effectieve manier om fouten te detecteren.

Conclusie

Het vinden van de juiste antwoorden in lineaire algebra vereist een combinatie van begrip, oefening en de juiste hulpmiddelen. Door de basisconcepten te beheersen, systematisch te werken, problemen te visualiseren en gebruik te maken van beschikbare hulpmiddelen, kun je je vaardigheden in lineaire algebra aanzienlijk verbeteren en het vertrouwen opbouwen om complexe problemen aan te pakken. Vergeet niet: oefening baart kunst! Blijf oefenen, wees geduldig en geef niet op. Met de juiste aanpak kun je lineaire algebra onder de knie krijgen en de vele toepassingen ervan ontdekken.