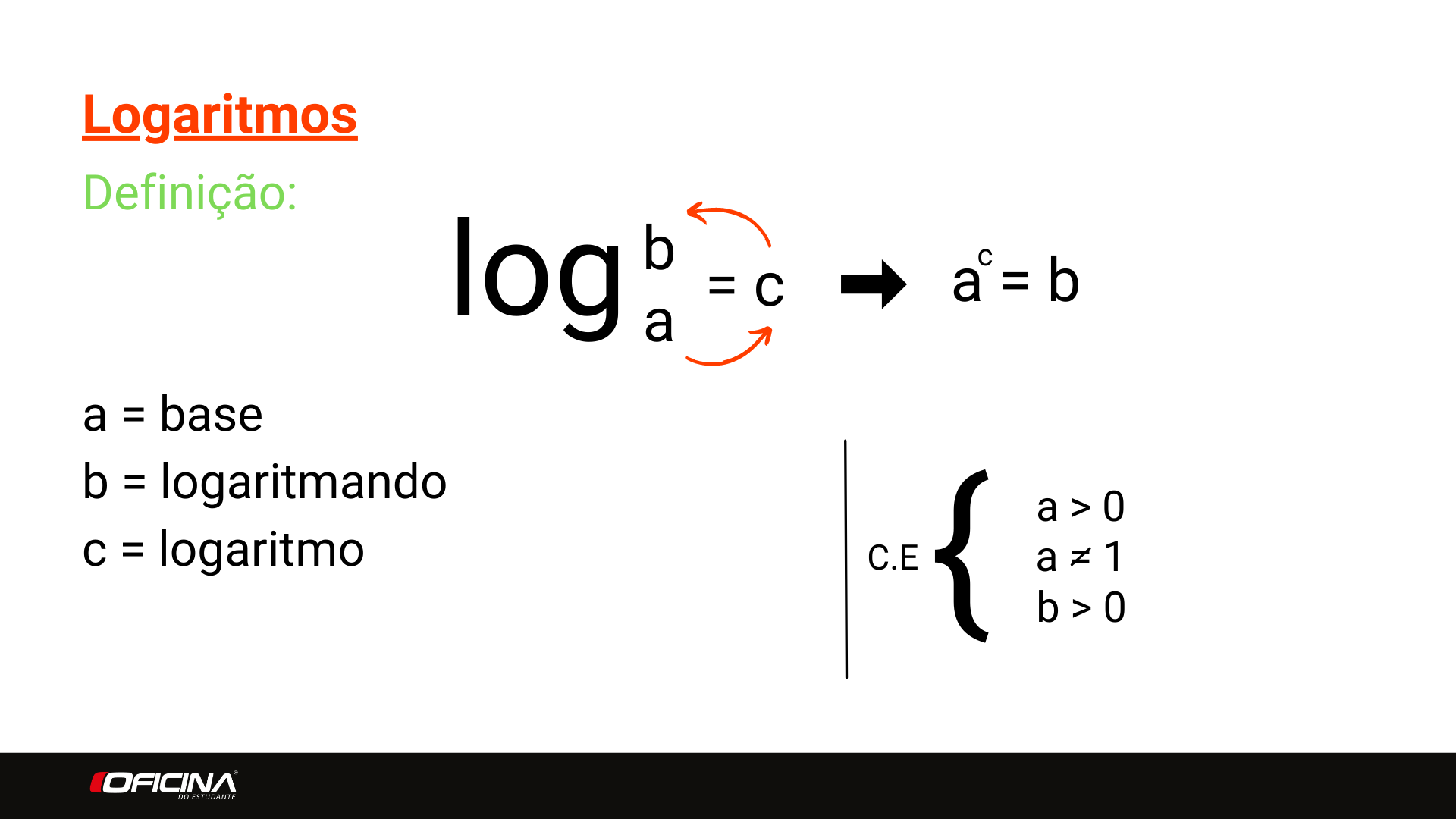
Log Rank Mantel Cox Test

We begrijpen het. Overlevingsanalyse kan ingewikkeld zijn. Je bent bezig met onderzoek, je verzamelt data over de tijd tot een bepaalde gebeurtenis – of het nu om herstel na een operatie gaat, de tijd tot een machine kapotgaat, of de levensduur van een product. En je wilt waardevolle inzichten halen uit die data. De Log-Rank (Mantel-Cox) test is een krachtig hulpmiddel in je arsenaal, maar de statistische complexiteit kan overweldigend zijn. Laten we proberen dit te vereenvoudigen en te laten zien hoe het jou kan helpen.

Dit artikel is bedoeld om de Log-Rank test te ontrafelen, niet alleen de theorie te bespreken, maar ook te laten zien hoe deze echt impact kan hebben op jouw werk en uiteindelijk, op de levens van mensen. We zullen ook ingaan op de kritiek en alternatieven, zodat je een weloverwogen beslissing kunt nemen over de toepassing van deze test.

Waarom is de Log-Rank test belangrijk?

Stel je voor: je bent onderzoeker in een ziekenhuis. Je bestudeert twee verschillende behandelingen voor een bepaalde vorm van kanker. Je hebt data verzameld over de overlevingstijd van patiënten die elke behandeling hebben ontvangen. Je wilt weten: is behandeling A echt beter dan behandeling B? Puur kijken naar de gemiddelde overlevingstijd is misleidend, omdat sommige patiënten wellicht langer leven puur door toeval, of door andere factoren die niet direct met de behandeling te maken hebben.

De Log-Rank test komt hier in beeld. Het is een statistische test die specifiek ontworpen is om twee of meer overlevingscurves te vergelijken. Het beoordeelt of er een significant verschil is in de overlevingstijden tussen de groepen, rekening houdend met de censurering van data (wanneer de studie eindigt voordat alle patiënten de gebeurtenis hebben meegemaakt, bijvoorbeeld overlijden). Censurering is cruciaal in overlevingsanalyse, en de Log-Rank test behandelt dit op een correcte manier.

Real-world impact

• Klinische studies: Bepalen of een nieuwe behandeling effectiever is dan de huidige standaardbehandeling. Dit kan leiden tot de goedkeuring van levensreddende medicijnen.
• Productontwikkeling: Vergelijken van de levensduur van verschillende ontwerpen of materialen. Denk aan het testen van de duurzaamheid van verschillende typen autobanden.
• Marketing: Analyseren van de retentie van klanten na verschillende marketingcampagnes. Welke campagne leidt tot de langste klantrelaties?
• Volksgezondheid: Evalueren van de impact van volksgezondheidscampagnes op de levensverwachting.

De impact van de Log-Rank test is dus breed en reikt veel verder dan alleen de statistische analyse. Het kan daadwerkelijk leiden tot betere behandelingen, betere producten en een betere volksgezondheid.

Hoe werkt de Log-Rank test?

De Log-Rank test werkt op basis van de nulhypothese dat er geen verschil is tussen de overlevingscurves van de groepen. Het berekent een teststatistiek (vaak een Chi-kwadraat waarde) die de verschillen tussen de waargenomen en verwachte aantal gebeurtenissen in elke groep samenvat. Een grote teststatistiek, en dus een kleine p-waarde, wijst erop dat de nulhypothese onwaarschijnlijk is, en dat er dus een significant verschil is tussen de overlevingscurves.

Denk aan twee roeiteams die een race varen. De Log-Rank test probeert te bepalen of er een daadwerkelijk verschil is in de snelheid van de teams, of dat het verschil puur toeval is (bijvoorbeeld, de wind stond gunstiger voor het ene team). De test kijkt niet alleen naar wie als eerste over de finishlijn komt, maar ook naar hoe snel elke roeier in elk team vaart gedurende de hele race, rekening houdend met eventuele uitvallers (censurering).

Belangrijke concepten:

• Hazard Ratio (HR): Een maat voor de relatieve kans op een gebeurtenis in de ene groep ten opzichte van de andere. Een HR van 2 betekent dat de kans op een gebeurtenis twee keer zo groot is in de ene groep.
• Kaplan-Meier curve: Een grafische weergave van de overlevingskans over de tijd. De Log-Rank test vergelijkt deze curves tussen groepen.
• P-waarde: De kans dat de waargenomen verschillen tussen de groepen zouden optreden als er geen daadwerkelijk verschil is. Een p-waarde kleiner dan een vooraf bepaald significantieniveau (bijvoorbeeld 0.05) wordt beschouwd als statistisch significant.

Counterpoints en alternatieven

Hoewel de Log-Rank test een krachtig hulpmiddel is, is het niet zonder kritiek. Een belangrijk punt is dat de Log-Rank test de aanname maakt dat de hazard ratio constant is over de tijd. Dit betekent dat het relatieve risico op een gebeurtenis hetzelfde moet blijven gedurende de hele studieperiode. Als deze aanname niet klopt, kan de Log-Rank test misleidende resultaten opleveren.

Bijvoorbeeld: stel dat een nieuwe behandeling voor kanker in eerste instantie zeer effectief is, maar na een tijdje minder effectief wordt. De hazard ratio zou dan niet constant zijn. In dergelijke gevallen zijn er alternatieve tests beschikbaar, zoals de Cox Proportional Hazards regressie, die rekening kan houden met tijdsafhankelijke covariaten.

Andere kritiekpunten en alternatieven omvatten:

• Gevoeligheid voor uitschieters: De Log-Rank test kan gevoelig zijn voor individuele gevallen met extreem lange of korte overlevingstijden. Alternatieven zoals de Wilcoxon test (gegeneraliseerde Kruskal-Wallis test) kunnen robuuster zijn in dergelijke situaties, omdat ze minder gewicht toekennen aan uitschieters. Echter, de Wilcoxon test is gevoeliger voor verschillen in overleving aan het *begin* van de follow-up periode, terwijl de Log-Rank test meer gewicht geeft aan verschillen aan het *einde*.
• Aanname van onafhankelijke censurering: De test gaat ervan uit dat de redenen voor censurering (bijvoorbeeld, patiënt trekt zich terug uit de studie) niet gerelateerd zijn aan de overlevingstijd. Als dit niet het geval is (bijvoorbeeld, patiënten die zich terugtrekken zijn significant zieker), kan dit de resultaten vertekenen. Het modelleren van censurering kan dan noodzakelijk zijn.
• Verschillende power bij verschillende patronen van verschillen: Zoals eerder genoemd, de Log-Rank test is optimal voor situaties waar de hazard ratio relatief constant is. Als de overlevingscurves kruisen (bijvoorbeeld, de ene behandeling is eerst beter, maar later slechter), kan de Log-Rank test een gebrek aan significantie laten zien, zelfs als er daadwerkelijk een verschil is. Tests die specifiek zijn ontworpen om kruisende curves te detecteren (zoals de Fleming-Harrington test) kunnen dan meer geschikt zijn.

Het is dus cruciaal om de aannames van de Log-Rank test te begrijpen en te evalueren of ze van toepassing zijn op jouw data. Als dat niet zo is, overweeg dan alternatieve methoden.

Een oplossing-gerichte aanpak

In plaats van alleen de problemen te benadrukken, willen we ook oplossingen bieden. Hier zijn enkele tips voor het effectief gebruik van de Log-Rank test:

• Controleer de aannames: Voordat je de Log-Rank test toepast, controleer de aanname van proportionele hazards. Dit kan grafisch worden gedaan door de Kaplan-Meier curves te plotten en visueel te beoordelen of ze parallel lopen. Er zijn ook formele statistische tests beschikbaar om de proportionele hazards aanname te beoordelen.
• Kies de juiste test: Als de aannames van de Log-Rank test niet kloppen, overweeg dan alternatieve testen zoals de Cox Proportional Hazards regressie, de Wilcoxon test of de Fleming-Harrington test.
• Rapporteer de resultaten duidelijk: Rapporteer de teststatistiek, de p-waarde, de hazard ratio en de 95% betrouwbaarheidsinterval. Geef ook een grafische weergave van de Kaplan-Meier curves.
• Interpreteer de resultaten in context: Beschouw de klinische relevantie van de resultaten. Een statistisch significant verschil is niet altijd klinisch significant.
• Overweeg andere covariaten: Houd rekening met andere factoren die de overleving kunnen beïnvloeden. Cox regressie kan worden gebruikt om de impact van deze covariaten te controleren.

Onthoud dat de Log-Rank test slechts een hulpmiddel is. Het is belangrijk om de resultaten te interpreteren in de context van je onderzoeksvraag en de beschikbare data. Werk samen met statistici of biostatistici om ervoor te zorgen dat je de test correct toepast en de resultaten correct interpreteert.

Voorbeeld van implementatie in R:

library(survival)
library(survminer)

# Maak een voorbeeld dataframe
df <- data.frame(
  time = c(10, 15, 20, 25, 30, 12, 18, 22, 28, 32),
  event = c(1, 1, 0, 1, 1, 1, 0, 1, 0, 1),
  group = c(rep("A", 5), rep("B", 5))
)

# Creëer een survival object
surv_object <- Surv(time = df$time, event = df$event)

# Fit het Kaplan-Meier model
fit <- survfit(surv_object ~ group, data = df)

# Voer de Log-Rank test uit
survdiff(surv_object ~ group, data = df)

# Visualiseer de Kaplan-Meier curves
ggsurvplot(fit, data = df, pval = TRUE, risk.table = TRUE)

Dit is een simpel voorbeeld. In de praktijk zal je dataset groter zijn en mogelijk complexere analyses vereisen. De survival package in R is een krachtig hulpmiddel voor overlevingsanalyse.

De sleutel tot succesvolle overlevingsanalyse ligt in het begrijpen van de data, de aannames van de methoden, en de interpretatie van de resultaten in de juiste context. Laat je niet ontmoedigen door de complexiteit. Met de juiste kennis en vaardigheden kan de Log-Rank test een waardevol hulpmiddel zijn om belangrijke inzichten te onthullen.

We hopen dat dit artikel je heeft geholpen om de Log-Rank test beter te begrijpen. Welke vraag over overlevingsanalyse houdt jou op dit moment het meest bezig?