Make A Box And Whisker Plot

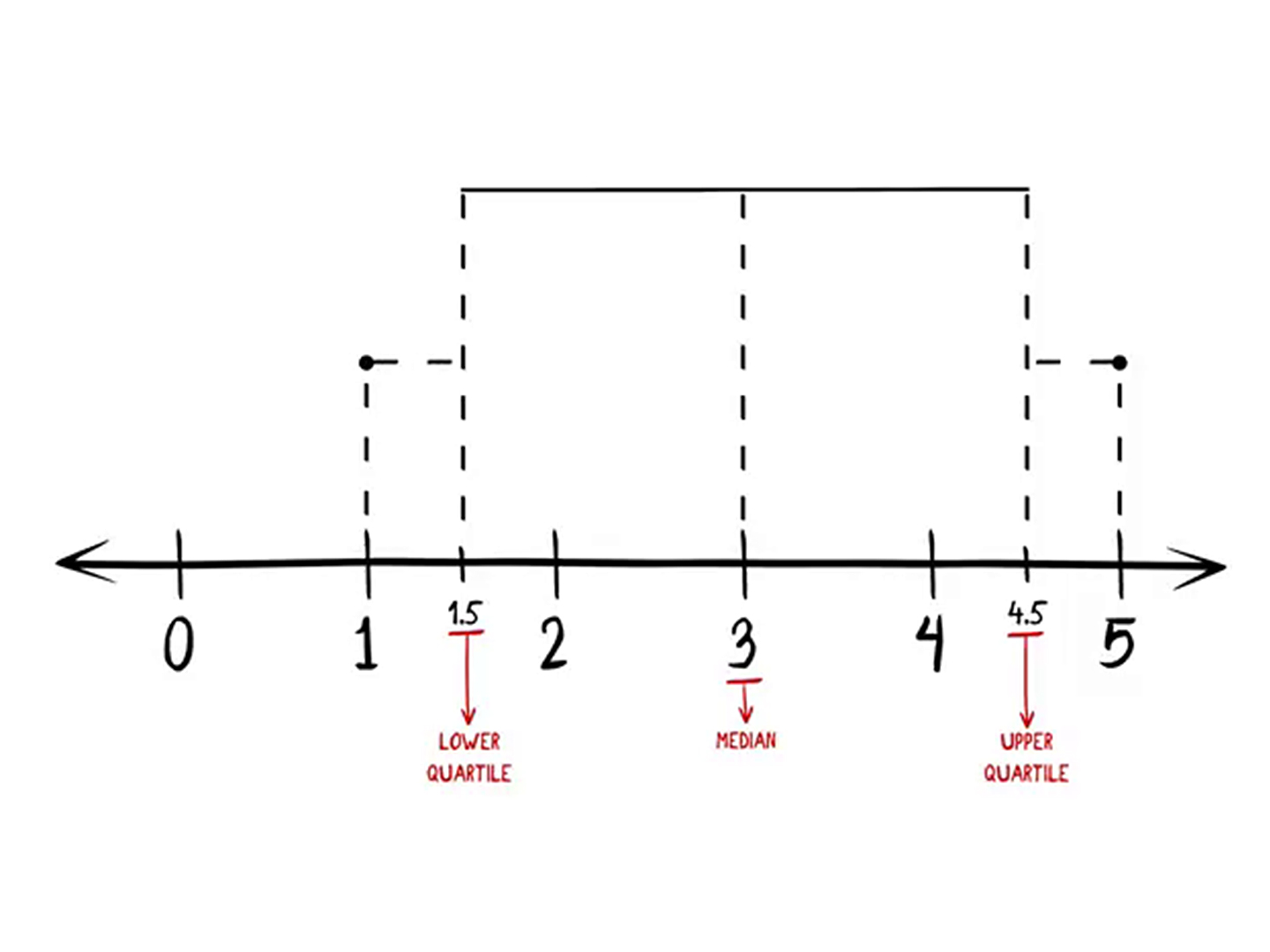
Een boxplot, ook wel bekend als een box-and-whisker plot, is een krachtig hulpmiddel voor het visualiseren van de verdeling van een dataset. Het biedt een snelle en overzichtelijke manier om de mediaan, kwartielen, en mogelijke uitbijters te identificeren. In dit artikel duiken we dieper in op de constructie en interpretatie van boxplots, zodat je zelf deze waardevolle grafische representatie kunt maken en begrijpen.

Waarom een Boxplot Gebruiken?

Boxplots zijn bijzonder nuttig in situaties waar je:

De spreiding van data wilt vergelijken tussen verschillende groepen.
Mogelijke uitbijters in een dataset wilt identificeren.
Snel een overzicht van de belangrijkste kenmerken van een verdeling nodig hebt, zonder te veel in detail te treden.

Voordelen van Boxplots

Boxplots bieden verschillende voordelen ten opzichte van andere visualisaties, zoals histogrammen of staafdiagrammen:

Compacte representatie: Ze vatten de belangrijkste kenmerken van een dataset samen in een enkele afbeelding.
Gemakkelijke vergelijking: Meerdere boxplots kunnen naast elkaar geplaatst worden om de verdelingen van verschillende datasets te vergelijken.
Uitbijterdetectie: Boxplots markeren uitbijters duidelijk, wat helpt bij het identificeren van ongebruikelijke waarden.

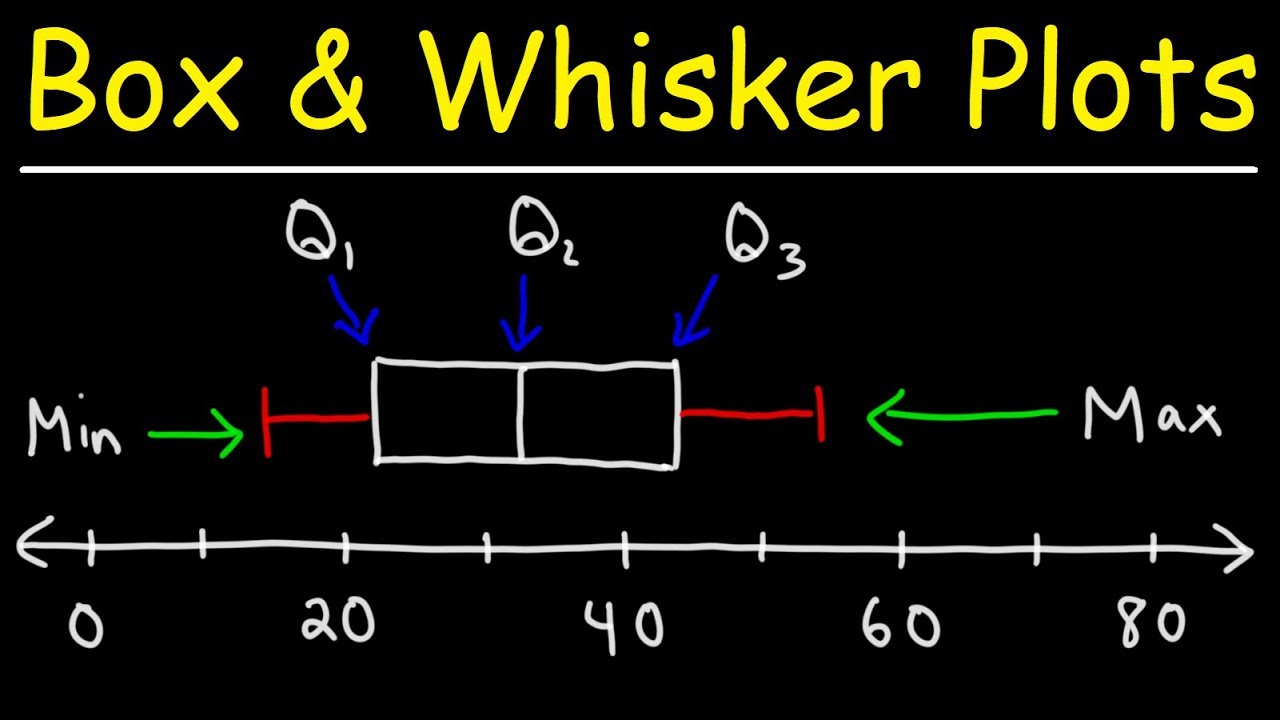
De Onderdelen van een Boxplot

Een boxplot bestaat uit verschillende essentiële componenten:

De Box (Doos)

De box zelf vertegenwoordigt het interkwartielbereik (IQR). De onderkant van de box markeert het eerste kwartiel (Q1), dat is de waarde waaronder 25% van de data valt. De bovenkant van de box markeert het derde kwartiel (Q3), de waarde waaronder 75% van de data valt. De lengte van de box (Q3 - Q1) geeft dus de spreiding van de middelste 50% van de data aan.

De Mediaan

Binnen de box bevindt zich een lijn die de mediaan (Q2) aangeeft. De mediaan is de middelste waarde in de dataset, wanneer deze van klein naar groot is geordend. De positie van de mediaan binnen de box kan ons vertellen over de scheefheid van de verdeling. Als de mediaan zich bijvoorbeeld dichter bij de onderkant van de box bevindt, is de verdeling waarschijnlijk rechtsscheef (positief scheef).

De Whiskers (Snorharen)

De whiskers strekken zich uit vanaf de box en geven de spreiding van de data buiten de box weer. De uiteinden van de whiskers worden bepaald door verschillende methoden, maar een veelgebruikte methode is de 1.5 * IQR-regel. Dit betekent dat de whiskers zich uitstrekken tot de meest extreme datawaarde die niet meer dan 1.5 keer het IQR onder Q1 of boven Q3 ligt. Datawaarden die verder liggen dan deze grenzen worden als uitbijters beschouwd en apart weergegeven (zie hieronder).

Uitbijters (Outliers)

Datawaarden die verder dan 1.5 * IQR onder Q1 of boven Q3 liggen, worden als uitbijters beschouwd en meestal weergegeven als individuele punten of kleine cirkels buiten de whiskers. Uitbijters kunnen wijzen op meetfouten, ongebruikelijke gebeurtenissen, of gewoon de natuurlijke variatie binnen de data. Het is belangrijk om uitbijters te onderzoeken en te bepalen of ze valide data zijn of dat ze verwijderd moeten worden (met de juiste voorzichtigheid en onderbouwing!).

Hoe Maak je een Boxplot?

Laten we de stappen doorlopen om een boxplot te maken. We gebruiken een fictieve dataset van de scores van studenten op een tentamen:

Data: 65, 70, 75, 80, 82, 85, 88, 90, 92, 95, 100, 40, 110

Sorteer de data: 40, 65, 70, 75, 80, 82, 85, 88, 90, 92, 95, 100, 110
Bereken de mediaan (Q2): Met 13 data punten is de mediaan de 7e waarde: 85.
Bereken het eerste kwartiel (Q1): Dit is de mediaan van de data onder de algemene mediaan (40, 65, 70, 75, 80, 82): (70+75)/2 = 72.5
Bereken het derde kwartiel (Q3): Dit is de mediaan van de data boven de algemene mediaan (88, 90, 92, 95, 100, 110): (92+95)/2 = 93.5
Bereken het Interkwartielbereik (IQR): IQR = Q3 - Q1 = 93.5 - 72.5 = 21
Bereken de grenzen voor uitbijters:
- Ondergrens: Q1 - (1.5 * IQR) = 72.5 - (1.5 * 21) = 41
- Bovengrens: Q3 - (1.5 * IQR) = 93.5 + (1.5 * 21) = 125
Identificeer uitbijters: De waarde 40 ligt onder de ondergrens (41), en de waarde 110 ligt niet buiten de bovengrens (125).
Bepaal de uiteinden van de whiskers:
- De onderste whisker loopt tot de laagste datawaarde die *niet* een uitbijter is, dus tot 65.
- De bovenste whisker loopt tot de hoogste datawaarde binnen de bovengrens, dus tot 110.

Nu kun je de boxplot tekenen:

Teken een verticale lijn.
Markeer Q1 (72.5) en Q3 (93.5) op de lijn en teken een rechthoek tussen deze punten.
Markeer de mediaan (85) binnen de box.
Teken de whiskers van de box tot 65 (onder) en 110 (boven).
Markeer de uitbijter (40) als een individueel punt onder de whisker.

Tegenwoordig worden boxplots meestal gemaakt met behulp van statistische software (zoals R, Python, SPSS) of spreadsheetprogramma's (zoals Excel). Deze tools automatiseren het proces en maken het gemakkelijk om boxplots te genereren voor grote datasets.

Real-World Voorbeelden

Vergelijken van Verkoopprestaties

Stel dat je de verkoopprestaties van verschillende verkoopteams wilt vergelijken. Je kunt boxplots gebruiken om de spreiding van de verkoopcijfers van elk team te visualiseren. De boxplot toont je de mediaanverkopen per team, de spreiding van de verkopen (IQR), en mogelijke uitschieters (bijvoorbeeld een teamlid dat exceptioneel goed presteert).

Analyse van Testresultaten

In het onderwijs kunnen boxplots worden gebruikt om de resultaten van verschillende klassen op een toets te vergelijken. De boxplot laat zien hoe de resultaten verdeeld zijn, of er sprake is van een grote spreiding, en of er leerlingen zijn die significant afwijken van de rest (zowel positief als negatief).

Onderzoek naar Klimaatverandering

Wetenschappers kunnen boxplots gebruiken om de temperatuurverschillen tussen verschillende jaren of locaties te visualiseren. De boxplot geeft een overzicht van de temperatuurspreiding, de mediane temperatuur, en mogelijke extreme temperatuurwaarden (hittegolven of koudegolven).

Conclusie en Actie

Boxplots zijn een onmisbaar hulpmiddel voor iedereen die met data werkt. Ze bieden een snelle en effectieve manier om de verdeling van een dataset te visualiseren, uitschieters te identificeren, en verschillende groepen te vergelijken. Experimenteer met verschillende datasets en softwarepakketten om vertrouwd te raken met het maken en interpreteren van boxplots. Door deze techniek te beheersen, kun je waardevolle inzichten uit je data halen en betere beslissingen nemen.

Aan de slag! Zoek een dataset die je interessant vindt, bijvoorbeeld via open data portalen. Gebruik een programma zoals Excel, Python met Matplotlib of Seaborn, of R om een boxplot te maken en de data te analyseren. Deel je bevindingen met collega's of vrienden om je begrip verder te verdiepen.