Modus Ponens And Modus Tollens

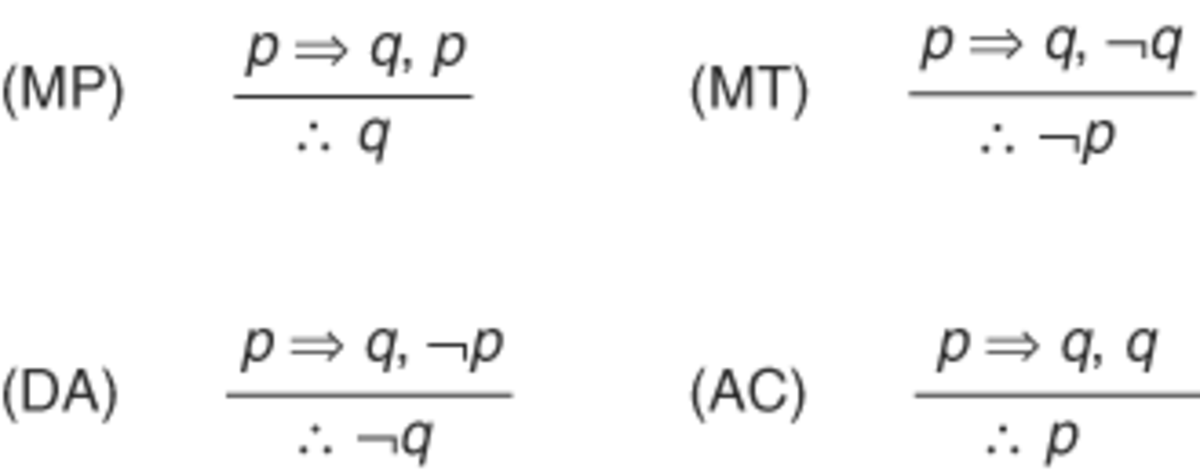
Heb je je ooit afgevraagd hoe je logisch kunt redeneren en geldige conclusies kunt trekken? Het lijkt soms alsof sommige mensen een ingebouwd kompas hebben voor waarheid, terwijl anderen verdwalen in verwarrende argumenten. Maar wat als ik je zou vertellen dat er eenvoudige, beproefde methoden zijn die je kunt gebruiken om je redeneervermogen aanzienlijk te verbeteren? Dit is waar Modus Ponens en Modus Tollens om de hoek komen kijken. Deze twee logische principes zijn krachtige hulpmiddelen die je helpen om je gedachten te ordenen, argumenten te evalueren en helderder te denken. Ze zijn fundamenteler dan je wellicht denkt en vormen de basis voor veel van onze dagelijkse beslissingen en redeneringen.

De Basis: Conditionele Uitspraken

Voordat we in Modus Ponens en Modus Tollens duiken, is het essentieel om te begrijpen wat een conditionele uitspraak is. Een conditionele uitspraak is een 'als... dan...' statement. Bijvoorbeeld: "Als het regent, dan wordt de straat nat."

In deze uitspraak is "het regent" de antecedent (het "als" gedeelte) en "de straat wordt nat" de consequent (het "dan" gedeelte). Het is cruciaal om te onthouden dat een conditionele uitspraak niet beweert dat de antecedent *altijd* waar is. Het zegt alleen dat *als* de antecedent waar is, *dan* zal de consequent ook waar zijn.

Laten we nu eens kijken naar hoe we deze conditionele uitspraken in onze logische toolbox kunnen gebruiken.

Modus Ponens: De Bevestigende Wijze

Modus Ponens, wat letterlijk "de manier van bevestigen" betekent in het Latijn, is een van de meest fundamentele en intuïtieve vormen van deductieve argumentatie. Het werkt als volgt:

1. Premisse 1: Als P, dan Q. (Bijvoorbeeld: Als het regent, dan wordt de straat nat.)
2. Premisse 2: P is waar. (Bijvoorbeeld: Het regent.)
3. Conclusie: Daarom is Q waar. (Daarom wordt de straat nat.)

Het mooie van Modus Ponens is dat als de premisen waar zijn, de conclusie noodzakelijk waar is. Er is geen ruimte voor twijfel. Het is een geldig argument.

Een praktisch voorbeeld: Stel je voor dat je een nieuwe espressomachine hebt gekocht. De handleiding zegt: "Als je de machine aanzet, dan licht het indicatielampje op." Je zet de machine aan (Premisse 2: P is waar). Wat kun je concluderen? Je kunt veilig concluderen dat het indicatielampje oplicht (Conclusie: Q is waar).

Waarom is dit belangrijk? Modus Ponens stelt ons in staat om voorspellingen te doen op basis van bestaande regels en waarnemingen. Het is de basis van veel van onze dagelijkse beslissingen. "Als ik nu vertrek, dan haal ik de trein." (Ik vertrek nu). "Dus, ik haal de trein."

Valstrikken en Misverstanden

Het is belangrijk om te onthouden dat Modus Ponens alleen werkt *als* de premisen waar zijn. Als een van de premisen onwaar is, is de conclusie mogelijk niet waar.

Voorbeeld: "Als ik de loterij win, dan koop ik een nieuwe auto." (Premisse 1). Ik win de loterij (Premisse 2). Dus, ik koop een nieuwe auto (Conclusie). Dit is Modus Ponens in actie. Maar wat als ik *niet* de loterij win? Dan is Premisse 2 onwaar, en de conclusie (dat ik een nieuwe auto koop) is niet noodzakelijk waar. Misschien koop ik de auto wel, misschien niet. De conditionele uitspraak garandeert alleen dat *als* ik win, ik een auto koop. Het zegt niets over wat er gebeurt als ik *niet* win.

Modus Tollens: De Ontkennende Wijze

Modus Tollens, wat "de manier van ontkennen" betekent, is een andere krachtige vorm van deductieve argumentatie. Het is iets minder intuïtief dan Modus Ponens, maar even belangrijk.

Het werkt als volgt:

1. Premisse 1: Als P, dan Q. (Bijvoorbeeld: Als het regent, dan wordt de straat nat.)
2. Premisse 2: Q is niet waar. (Bijvoorbeeld: De straat is niet nat.)
3. Conclusie: Daarom is P niet waar. (Daarom regent het niet.)

In Modus Tollens ontkennen we de *consequent* van de conditionele uitspraak om te concluderen dat de *antecedent* ook onwaar moet zijn. Als de premisen waar zijn, is de conclusie geldig.

Een praktisch voorbeeld: Je hebt een slimme thermostaat in huis. Je hebt hem geprogrammeerd om de verwarming aan te zetten "als de temperatuur onder de 18 graden Celsius komt." (Premisse 1). Je loopt de kamer binnen en de verwarming staat *niet* aan (Premisse 2). Wat kun je concluderen? Je kunt concluderen dat de temperatuur *niet* onder de 18 graden Celsius is gekomen (Conclusie).

Waarom is dit belangrijk? Modus Tollens is bijzonder nuttig om hypotheses te weerleggen en beweringen te falsificeren. In de wetenschap wordt het gebruikt om theorieën te testen. "Als mijn theorie klopt, dan zal ik X waarnemen." "Ik heb X *niet* waargenomen." "Dus, mijn theorie is waarschijnlijk onjuist (of moet worden aangepast)."

Valstrikken en Misverstanden

Een veel voorkomende fout bij het gebruik van Modus Tollens is het verwarren met de ontkenning van de antecedent. Dit is een ongeldige redenering.

De Ontkenning van de Antecedent (Ongeldig):

1. Premisse 1: Als P, dan Q.
2. Premisse 2: P is niet waar.
3. Conclusie: Daarom is Q niet waar.

Voorbeeld: "Als het regent, dan wordt de straat nat." Het regent *niet*. Daarom wordt de straat *niet* nat. Deze redenering is ongeldig! De straat kan ook nat worden door bijvoorbeeld een sproeier of een lek.

Het verschil tussen Modus Tollens en de ontkenning van de antecedent is cruciaal. Modus Tollens beweert dat *als* de consequent onwaar is, de antecedent *moet* onwaar zijn. De ontkenning van de antecedent beweert dat *als* de antecedent onwaar is, de consequent *moet* onwaar zijn, wat niet noodzakelijk het geval is.

Modus Ponens en Modus Tollens in het Dagelijks Leven

Hoewel deze logische principes misschien abstract lijken, gebruiken we ze voortdurend in ons dagelijks leven, vaak zonder erbij na te denken.

• Probleemoplossing: "Als ik dit probleem wil oplossen, dan moet ik eerst X doen." Ik wil het probleem oplossen, dus ik doe X (Modus Ponens). "Als dit de oorzaak van het probleem is, dan zou ik Y moeten zien." Ik zie Y *niet*, dus dit is waarschijnlijk *niet* de oorzaak (Modus Tollens).
• Besluitvorming: "Als ik deze investering doe, dan hoop ik rendement Z te behalen." Ik heb rendement Z *niet* behaald, dus misschien was de investering geen goede keuze (Modus Tollens). "Als ik deze vaardigheid leer, dan kan ik een betere baan krijgen." Ik leer de vaardigheid, dus ik verwacht een betere baan te kunnen vinden (Modus Ponens).
• Communicatie: Het herkennen van Modus Ponens en Modus Tollens in de argumenten van anderen stelt je in staat om deze argumenten kritisch te evalueren en te bepalen of ze geldig zijn.

Conclusie: Logisch Redeneren als Vaardigheid

Modus Ponens en Modus Tollens zijn fundamentele bouwstenen van logisch redeneren. Door deze principes te begrijpen en toe te passen, kun je je denken verscherpen, argumenten effectiever evalueren en betere beslissingen nemen. Het is een vaardigheid die je kunt leren en perfectioneren, net als elke andere vaardigheid. Door bewust aandacht te besteden aan de structuur van je argumenten en de argumenten van anderen, kun je valstrikken vermijden en je redeneervermogen aanzienlijk verbeteren. Oefen met het identificeren van Modus Ponens en Modus Tollens in verschillende contexten, en je zult versteld staan van de impact die deze eenvoudige principes kunnen hebben op je leven.