Omtrek Berekenen Van Een Cirkel

Heb je je ooit afgevraagd hoe ze de afstand rond een pannenkoek meten, of hoe je de hoeveelheid hekwerk berekent die je nodig hebt voor een rond bloemperk? Het antwoord ligt in het berekenen van de omtrek van een cirkel. Dit artikel is speciaal geschreven voor iedereen die nieuw is in de wiskunde, van studenten tot hobbyisten, en biedt een heldere en praktische gids voor dit fundamentele concept.

Wat is de Omtrek van een Cirkel?

De omtrek van een cirkel is niets meer dan de totale afstand rond de buitenkant. Stel je voor dat je een touwtje rond een pizzabodem legt – de lengte van dat touwtje is de omtrek.

Waarom is dit belangrijk?

Het berekenen van de omtrek is verrassend nuttig in het dagelijks leven, zoals:

• Hekwerk plaatsen: Bepalen hoeveel hekwerk nodig is voor een cirkelvormige tuin.
• Pizza snijden: Begrijpen hoeveel korst iedereen krijgt.
• Fietsen: De afstand berekenen die een fiets aflegt per wielomwenteling.
• Constructie: Het plannen en bouwen van ronde structuren zoals koepels en tunnels.

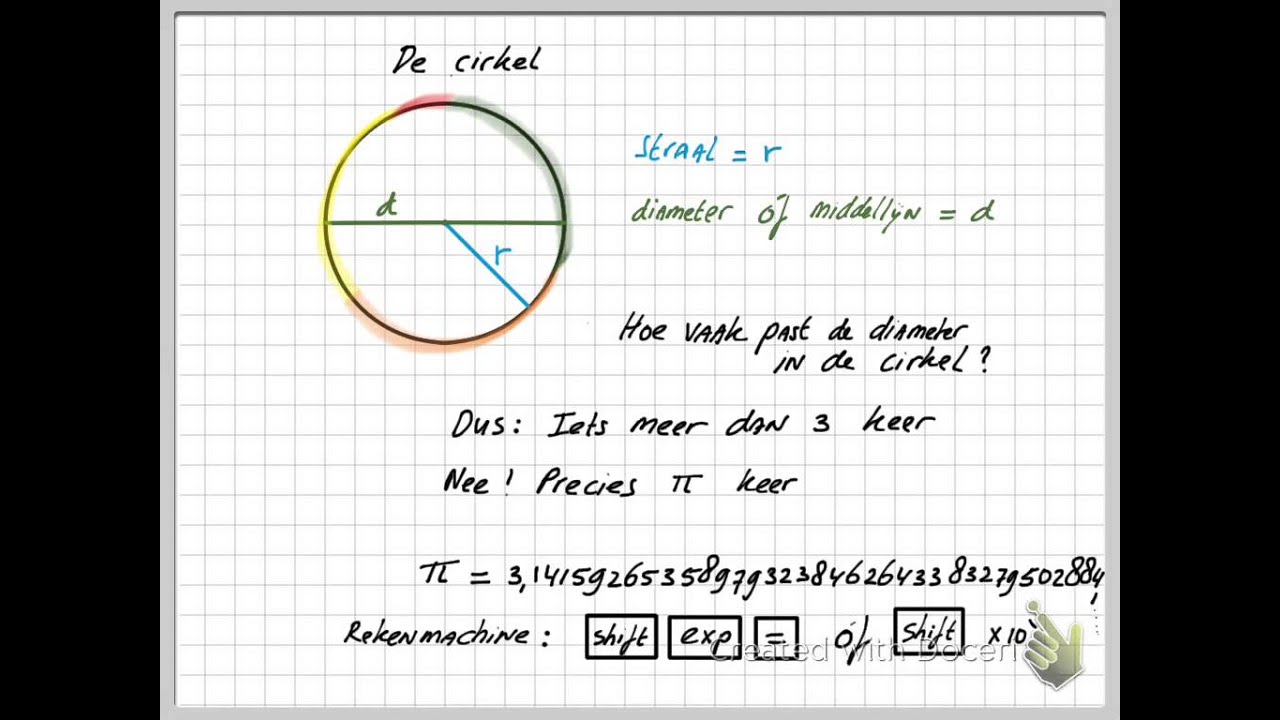
De Formule: Omtrek = πd = 2πr

De omtrek van een cirkel kan berekend worden met de volgende formule:

Omtrek = πd

Of, als je de straal (radius) weet:

Omtrek = 2πr

Laten we deze elementen eens bekijken:

• π (pi): Dit is een constante waarde, ongeveer gelijk aan 3.14159. Voor de meeste praktische doeleinden kun je 3.14 gebruiken.
• d (diameter): De diameter is de afstand door het midden van de cirkel, van de ene kant naar de andere. Het is twee keer de straal.
• r (radius/straal): De straal is de afstand van het middelpunt van de cirkel tot de rand.

Stap-voor-Stap Uitleg met Voorbeelden

Laten we eens kijken hoe we deze formule in de praktijk kunnen gebruiken met een paar voorbeelden:

Voorbeeld 1: Gegeven Diameter

Stel dat je een ronde tafel hebt met een diameter van 1 meter. Wat is de omtrek van de tafel?

1. Identificeer de gegeven waarde: De diameter (d) = 1 meter.
2. Gebruik de formule: Omtrek = πd
3. Vul de waarden in: Omtrek = 3.14 * 1 meter
4. Bereken het resultaat: Omtrek = 3.14 meter

Dus, de omtrek van de tafel is 3.14 meter.

Voorbeeld 2: Gegeven Straal

Stel dat je een cirkelvormig bloemperk hebt met een straal van 2 meter. Hoeveel hekwerk heb je nodig om er omheen te plaatsen?

1. Identificeer de gegeven waarde: De straal (r) = 2 meter.
2. Gebruik de formule: Omtrek = 2πr
3. Vul de waarden in: Omtrek = 2 * 3.14 * 2 meter
4. Bereken het resultaat: Omtrek = 12.56 meter

Je hebt dus 12.56 meter hekwerk nodig.

Voorbeeld 3: Een iets ingewikkeldere situatie

Een fietswiel heeft een straal van 35 cm. Hoeveel meter legt de fiets af na 10 omwentelingen van het wiel?

1. Identificeer de gegeven waarde: De straal (r) = 35 cm.
2. Bereken de omtrek van het wiel: Omtrek = 2πr = 2 * 3.14 * 35 cm = 219.8 cm
3. Bereken de totale afstand na 10 omwentelingen: Totale afstand = 10 * 219.8 cm = 2198 cm
4. Converteer naar meters: 2198 cm / 100 = 21.98 meter

De fiets legt dus 21.98 meter af na 10 omwentelingen van het wiel.

Praktische Tips en Trucs

• Gebruik een rekenmachine: Voor meer nauwkeurige berekeningen, gebruik een rekenmachine met een π-knop.
• Rond af: Voor praktische toepassingen is het vaak voldoende om π af te ronden tot 3.14.
• Meet nauwkeurig: Hoe nauwkeuriger je de diameter of straal meet, hoe nauwkeuriger je omtrekberekening zal zijn.
• Denk in eenheden: Let goed op de eenheden (meters, centimeters, etc.) en zorg ervoor dat je consistent bent.

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Hier zijn een paar veelvoorkomende fouten die mensen maken bij het berekenen van de omtrek:

• Straal en diameter verwarren: Zorg ervoor dat je weet of je de straal of de diameter hebt. De diameter is twee keer de straal.
• Verkeerde waarde voor π gebruiken: Gebruik 3.14 of de π-knop op je rekenmachine voor een nauwkeurige berekening.
• Verkeerde eenheden gebruiken: Zorg ervoor dat alle metingen in dezelfde eenheden zijn voordat je gaat rekenen. Als de straal in centimeters is, moet de omtrek ook in centimeters zijn.
• Vergeten de formule te gebruiken: Zorg ervoor dat je de juiste formule gebruikt: Omtrek = πd of Omtrek = 2πr.

Waarom Pi (π) Zo Speciaal is

Pi (π) is een irrationeel getal, wat betekent dat het een oneindige, niet-herhalende decimale representatie heeft. Het is ongeveer 3.14159265358979323846... en gaat oneindig door. Het is een van de meest fundamentele constanten in de wiskunde en komt voor in veel verschillende formules en toepassingen, niet alleen bij het berekenen van de omtrek van een cirkel.

De ontdekking en studie van π gaat duizenden jaren terug, met vroege benaderingen door de Babyloniërs en Egyptenaren. Archimedes was een van de eersten die een nauwkeurige manier bedacht om π te benaderen, en sindsdien hebben wiskundigen over de hele wereld hun steentje bijgedragen aan ons begrip van dit fascinerende getal.

Andere Toepassingen van de Omtrek Berekening

Buiten de eerder genoemde voorbeelden, duikt de omtrek berekening op in nog veel meer situaties:

• Ontwerpen van wielen en tandwielen: Bij het ontwerpen van machines is de omtrek van wielen en tandwielen cruciaal voor het bepalen van de overbrengingsverhoudingen en de snelheid van beweging.
• Navigatie: Bij het berekenen van afstanden op de aarde, die we benaderen als een bol, speelt de omtrek een belangrijke rol.
• Astronomie: Bij het berekenen van de baan van planeten en satellieten rond sterren.
• Maken van sieraden: Bij het maken van armbanden en halskettingen met ronde elementen.

Oefenen Baart Kunst

De beste manier om de formule voor de omtrek van een cirkel onder de knie te krijgen, is door te oefenen. Zoek online naar oefenopgaven, of bedenk zelf scenario's waarin je de omtrek moet berekenen. Hoe meer je oefent, hoe makkelijker het zal worden.

Conclusie

Het berekenen van de omtrek van een cirkel is een fundamentele vaardigheid met verrassend veel praktische toepassingen. Met de eenvoudige formule Omtrek = πd of Omtrek = 2πr, kun je de afstand rond elke cirkelvormige vorm berekenen. Onthoud: oefening baart kunst! Dus pak je rekenmachine en meetlint en ga aan de slag! We hopen dat dit artikel je heeft geholpen om dit belangrijke concept beter te begrijpen. Nu kun jij met vertrouwen de omtrek van cirkels berekenen en deze kennis toepassen in allerlei situaties!