Omtrek Cirkel Berekenen Met Straal

Ken je dat? Je staat in de keuken, kijkt naar die prachtige taartvorm en vraagt je af: hoeveel lint heb ik eigenlijk nodig om hier helemaal omheen te strikken? Of misschien ben je bezig met een knutselproject, een tuinontwerp, of zelfs een wiskundige uitdaging op school. De vraag blijft: hoe bereken ik de omtrek van die cirkel?

Je bent niet de enige! Velen worstelen met dit probleem. Het lijkt misschien een abstracte wiskundige formule, maar het heeft zoveel praktische toepassingen in ons dagelijks leven. Laten we samen eens kijken hoe we dit kunnen aanpakken.

Waarom de Omtrek van een Cirkel Belangrijk Is

Laten we eerlijk zijn, wiskunde kan soms voelen als een ver-van-mijn-bedshow. Maar de waarheid is dat de omtrek van een cirkel, en de formule om deze te berekenen, cruciaal is in veel verschillende gebieden:

Techniek en Architectuur: Denk aan het ontwerpen van wielen, leidingen, koepels of bruggen. Een accurate berekening van de omtrek is essentieel voor de structurele integriteit en functionaliteit.
Vervaardiging: Van het maken van blikjes soep tot het ontwerpen van pizza’s, de omtrek speelt een rol in materiaalkosten en efficiëntie.
Navigatie: GPS-systemen en andere navigatiehulpmiddelen gebruiken cirkels en hun eigenschappen om afstanden en routes te berekenen.
Alledaagse situaties: Zoals eerder genoemd, van het inschatten van de benodigde hoeveelheid lint voor een cadeau tot het plannen van een bloembed in je tuin.

Zonder deze basiskennis zou een groot deel van de technologie en infrastructuur die we dagelijks gebruiken simpelweg niet bestaan.

De Basis: Straal, Diameter en Pi (π)

Voordat we de formule induiken, moeten we een paar belangrijke concepten helder hebben:

Straal (r): De afstand van het middelpunt van de cirkel tot een punt op de rand.
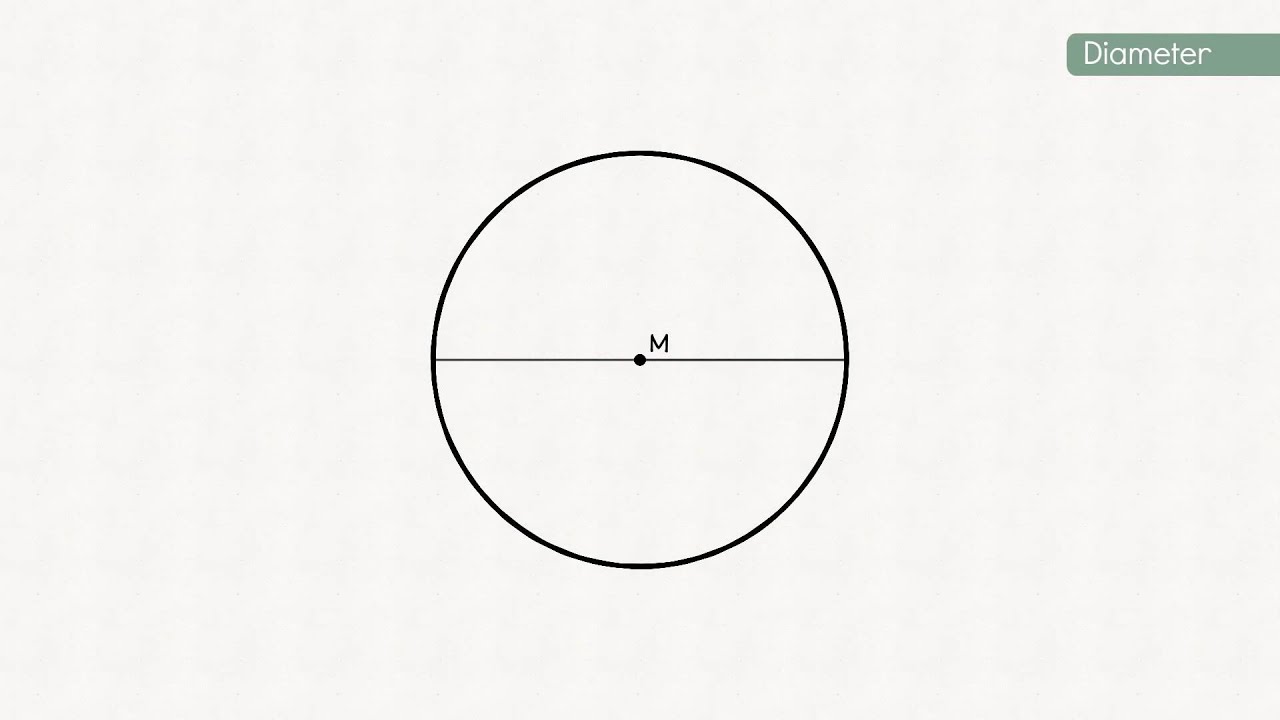
Diameter (d): De afstand over de cirkel, door het middelpunt. De diameter is twee keer de straal (d = 2r).
Pi (π): Een constante waarde, ongeveer gelijk aan 3,14159. Pi is de verhouding tussen de omtrek van een cirkel en zijn diameter.

Je kunt Pi zien als een magisch getal dat de omtrek en de diameter van elke cirkel, ongeacht de grootte, met elkaar verbindt. Het is een fundamenteel getal in de wiskunde en komt overal voor, van geometrie tot kansberekening.

De Formule: Omtrek = 2πr of πd

Hier komt de formule waar je op hebt gewacht:

Omtrek = 2 * π * straal of Omtrek = π * diameter

Laten we deze eens ontleden:

2πr: Je vermenigvuldigt 2 met Pi (π) en vervolgens met de straal (r) van de cirkel.
πd: Je vermenigvuldigt Pi (π) met de diameter (d) van de cirkel.

Beide formules geven hetzelfde resultaat. Je gebruikt de formule die het makkelijkst is op basis van de informatie die je hebt. Heb je de straal? Gebruik dan 2πr. Heb je de diameter? Gebruik dan πd.

Voorbeeld: Stel je voor dat je een cirkel hebt met een straal van 5 cm. De omtrek zou dan zijn: 2 * 3,14159 * 5 = 31,4159 cm. Als je de diameter zou hebben (10 cm), dan zou de omtrek zijn: 3,14159 * 10 = 31,4159 cm. Precies hetzelfde!

Een Praktische Benadering: Stappenplan voor het Berekenen van de Omtrek

Hier is een stapsgewijze handleiding om je te helpen de omtrek van een cirkel te berekenen:

Identificeer de straal of diameter: Lees het probleem zorgvuldig. Wordt de straal of de diameter gegeven? Soms moet je een beetje detectivewerk verrichten.
Kies de juiste formule: Gebruik 2πr als je de straal hebt en πd als je de diameter hebt.
Vervang de waarden: Vervang de letters in de formule door de overeenkomstige getallen. Gebruik 3,14159 voor π, of gebruik de π-knop op je rekenmachine voor een nauwkeuriger resultaat.
Vermenigvuldig: Voer de vermenigvuldiging uit. Zorg ervoor dat je de juiste volgorde van bewerkingen volgt.
Noteer de eenheden: Vergeet niet de eenheden toe te voegen aan je antwoord. Als de straal in centimeters is, is de omtrek ook in centimeters.

Tip: Als je geen rekenmachine bij de hand hebt, kun je π afronden op 3,14 voor een snelle schatting. Dit is vaak voldoende voor alledaagse toepassingen.

Mogelijke Valkuilen en Hoe Ze Te Vermijden

Soms gaat het niet helemaal vlekkeloos. Hier zijn een paar veelvoorkomende fouten en hoe je ze kunt voorkomen:

Straal en diameter verwarren: Onthoud dat de diameter twee keer de straal is. Lees de vraag aandachtig!
Verkeerde formule gebruiken: Zorg ervoor dat je de juiste formule gebruikt op basis van de beschikbare informatie.
Pi vergeten: Pi is essentieel voor de berekening. Vergeet het niet!
Eenheden vergeten: Een getal zonder eenheden is als een verhaal zonder einde. Voeg altijd de juiste eenheden toe aan je antwoord.
Verkeerde volgorde van bewerkingen: Volg de regels van de wiskunde. Vermenigvuldig voordat je optelt (in dit geval, vermenigvuldigingen eerst!).

De Discussie: Is Pi Echt 3,14?

Je hoort vaak dat Pi gelijk is aan 3,14. Maar is dat wel zo? Het korte antwoord is nee. Pi is een irrationeel getal, wat betekent dat het een oneindige, niet-herhalende decimale uitbreiding heeft. 3,14 is slechts een benadering. Voor de meeste alledaagse berekeningen is 3,14 prima, maar voor meer nauwkeurige berekeningen (zoals in de wetenschap of techniek) is het belangrijk om een nauwkeurigere waarde te gebruiken, of de π-knop op je rekenmachine te gebruiken.

Sommigen beweren dat het gebruik van een benadering van Pi de resultaten onnauwkeurig maakt. Dit is waar, maar de impact is vaak minimaal, vooral bij kleine cirkels. De relevantie van de nauwkeurigheid hangt af van de context. Voor het bakken van een taart maakt het waarschijnlijk weinig uit of je Pi afrondt, maar voor het bouwen van een brug kan het wel een significant verschil maken.

De Kracht van Visualisatie: Cirkels in het Echt

Om de formule echt te begrijpen, kan het helpen om de cirkel in de echte wereld te visualiseren. Denk aan een fietswiel. De straal is de afstand van de naaf tot de band. De omtrek is de afstand die de fiets aflegt bij één volledige omwenteling van het wiel. Door deze verbanden te zien, wordt de abstracte formule plotseling veel concreter.

Probeer zelf eens wat objecten met een cirkelvormige doorsnede op te meten. Gebruik een meetlint om de omtrek direct te meten, en meet vervolgens de diameter. Deel de omtrek door de diameter. Wat krijg je? Als je het nauwkeurig genoeg hebt gemeten, zou je een getal in de buurt van 3,14 moeten krijgen! Dit is een leuke manier om de formule in de praktijk te ervaren en te zien hoe Pi "werkt".

Verder dan de Basis: Geavanceerde Toepassingen

De omtrek van een cirkel is slechts het begin. Deze kennis kan worden gebruikt om complexere problemen op te lossen, zoals:

Oppervlakte van een cirkel: De oppervlakte is gerelateerd aan de straal en wordt berekend met de formule: Oppervlakte = πr².
Volume van een cilinder: Het volume is gerelateerd aan de oppervlakte van de basis (een cirkel) en de hoogte van de cilinder: Volume = πr²h.
Booglengte: Een deel van de omtrek van een cirkel. De booglengte kan worden berekend als je de hoek van de boog kent.

Door de basisprincipes van de omtrek te begrijpen, open je de deur naar een hele wereld van wiskundige en wetenschappelijke toepassingen.

Conclusie: Omtrek Berekenen is Makkelijker Dan Je Denkt!

Hopelijk heb je nu een beter begrip van hoe je de omtrek van een cirkel kunt berekenen. Het is een fundamentele vaardigheid die op veel verschillende manieren van pas kan komen. Met de juiste kennis en oefening, zul je in staat zijn om cirkels te overwinnen, of het nu gaat om het versieren van een taart of het ontwerpen van een complex technisch project.

Dus, wat ga jij vandaag met je nieuwe kennis doen? Welke cirkel ga jij als eerste berekenen?