Omtrek Van Een Cirkel Berekenen

Heb je ooit naar een perfect ronde pizza gekeken en je afgevraagd hoeveel korst er precies omheen zit? Of misschien probeerde je te bepalen hoeveel hekwerk je nodig hebt voor een rond bloemperk? Het berekenen van de omtrek van een cirkel – de afstand rondom de cirkel – is een fundamentele vaardigheid die verrassend vaak van pas komt. Vaak voelt dit als een abstracte wiskundeles, maar in werkelijkheid is het een praktische tool die je in talloze situaties kunt gebruiken.

Laten we eerlijk zijn: wiskunde kan soms intimiderend zijn. Al die formules en symbolen… het kan je duizelen. Maar vrees niet! Dit artikel is bedoeld om het berekenen van de omtrek van een cirkel te demystificeren. We zullen het stap voor stap uitleggen, met duidelijke voorbeelden en zonder ingewikkeld jargon. We begrijpen dat je misschien niet de volgende Einstein bent, en dat is helemaal prima. Ons doel is om je de tools te geven om zelfverzekerd de omtrek van elke cirkel te kunnen berekenen.

Waarom is de Omtrek van een Cirkel Belangrijk?

De impact van deze kennis reikt veel verder dan alleen schoolwerk. Denk eens aan:

Architectuur en Design: Architecten en ontwerpers gebruiken cirkels en bogen in hun ontwerpen. De omtrek berekenen is cruciaal voor het bepalen van materialen en afmetingen.
Techniek: Ingenieurs gebruiken de omtrek van cirkels bij het ontwerpen van wielen, pijpleidingen en andere circulaire componenten.
Koken en Bakken: Zoals we al zeiden: pizza! Maar ook taarten, pannenkoeken en andere ronde lekkernijen vereisen dat je de omtrek kunt inschatten of berekenen, bijvoorbeeld bij het bepalen van de juiste hoeveelheid glazuur.
Tuinieren: Het plannen van een rond bloemperk of een vijver vereist het berekenen van de omtrek om te bepalen hoeveel aarde, randafwerking of folie je nodig hebt.
Alledaagse Problemen: Van het bepalen van de afstand die een wiel aflegt in één rotatie tot het inschatten van de hoeveelheid lint die je nodig hebt voor een rond cadeau, de omtrek van een cirkel komt vaker voor dan je denkt.

Dus, hoewel het misschien lijkt op een abstract wiskundig concept, is het berekenen van de omtrek van een cirkel eigenlijk een zeer praktische vaardigheid met toepassingen in een breed scala aan vakgebieden en alledaagse situaties.

De Formule: C = πd of C = 2πr

De formule voor het berekenen van de omtrek van een cirkel is eigenlijk vrij eenvoudig:

C = πd

Of:

C = 2πr

Waar:

C staat voor de omtrek (circumference in het Engels).
π (pi) is een wiskundige constante die ongeveer gelijk is aan 3,14159. Voor de meeste praktische doeleinden kun je 3,14 gebruiken.
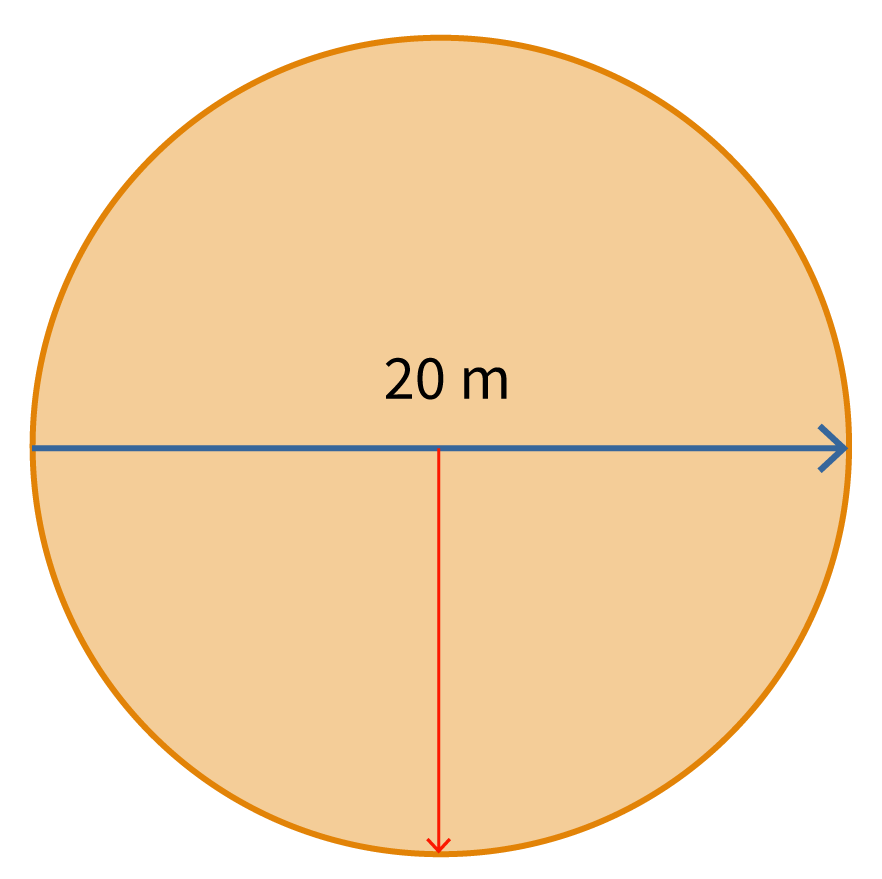
d staat voor de diameter van de cirkel (de afstand van de ene kant van de cirkel naar de andere kant, door het middelpunt).
r staat voor de straal van de cirkel (de afstand van het middelpunt van de cirkel tot de rand). De straal is de helft van de diameter.

Laten we dit verder uitpakken:

Denk aan een taart. De diameter is een snede die recht door het midden van de taart gaat, van de ene rand naar de andere. De straal is een snede van het midden van de taart tot de rand.

Dus, als je de diameter van een cirkel weet, vermenigvuldig je die simpelweg met π (ongeveer 3,14) om de omtrek te vinden. Als je de straal weet, vermenigvuldig je die eerst met 2 (om de diameter te vinden) en vermenigvuldig je vervolgens met π.

Voorbeeld 1: De Pizza

Stel, je hebt een pizza met een diameter van 30 cm. Wat is de omtrek van de pizza?

We kennen de diameter: d = 30 cm.
We gebruiken de formule: C = πd.
We vullen de waarden in: C = 3,14 * 30 cm.
We berekenen: C = 94,2 cm.

Dus, de omtrek van de pizza is ongeveer 94,2 cm. Dat is de lengte van de korst die je gaat eten!

Voorbeeld 2: Het Bloemperk

Je wilt een rond bloemperk aanleggen met een straal van 1,5 meter. Hoeveel randafwerking heb je nodig?

We kennen de straal: r = 1,5 meter.
We gebruiken de formule: C = 2πr.
We vullen de waarden in: C = 2 * 3,14 * 1,5 meter.
We berekenen: C = 9,42 meter.

Je hebt ongeveer 9,42 meter randafwerking nodig voor je bloemperk.

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Hier zijn enkele veelgemaakte fouten bij het berekenen van de omtrek van een cirkel, en hoe je ze kunt vermijden:

De straal en de diameter verwarren: Onthoud dat de straal de helft van de diameter is. Zorg ervoor dat je de juiste waarde gebruikt in de formule. Als je de straal hebt, moet je deze verdubbelen om de diameter te krijgen.
De verkeerde formule gebruiken: Gebruik C = πd als je de diameter kent, en C = 2πr als je de straal kent.
De waarde van π vergeten: Vergeet niet dat π ongeveer 3,14 is. Gebruik deze waarde in je berekening. Sommige rekenmachines hebben een π-knop, wat nog nauwkeuriger is.
Vergeet de eenheden niet: Zorg ervoor dat je de juiste eenheden gebruikt (bijvoorbeeld cm, meter, inch) en dat je consistent bent. Als de diameter in centimeters is, dan is de omtrek ook in centimeters.

Tegenargumenten en Nuances

Sommige mensen beweren dat het berekenen van de omtrek van een cirkel niet relevant is in het moderne tijdperk, omdat computers en software deze berekeningen automatisch kunnen uitvoeren. Hoewel dit waar is in bepaalde contexten (zoals CAD-software), is het belangrijk om de fundamentele principes te begrijpen. Het stelt je in staat om schattingen te maken, fouten te controleren en een dieper begrip te ontwikkelen van de wereld om je heen. Bovendien heb je niet altijd een computer of software tot je beschikking.

Een ander tegenargument is dat π een irrationeel getal is, wat betekent dat het een oneindig aantal decimalen heeft en dus nooit exact kan worden berekend. Dit is waar, maar voor de meeste praktische toepassingen is het voldoende om 3,14 te gebruiken of een rekenmachine met een π-knop. De resulterende fout is meestal verwaarloosbaar.

Oefening Baart Kunst

De beste manier om het berekenen van de omtrek van een cirkel onder de knie te krijgen, is door te oefenen. Hier zijn een paar oefenopgaven:

Een cirkel heeft een diameter van 10 cm. Wat is de omtrek?
Een cirkel heeft een straal van 7 meter. Wat is de omtrek?
Een wiel heeft een omtrek van 157 cm. Wat is de diameter van het wiel? (Hint: je moet de formule omdraaien!)

Probeer deze opgaven op te lossen en controleer je antwoorden met een rekenmachine. Naarmate je meer oefent, zul je merken dat het berekenen van de omtrek van een cirkel steeds gemakkelijker en intuïtiever wordt.

Andere Methoden voor het Berekenen van de Omtrek

Hoewel de formules C = πd en C = 2πr de meest gebruikelijke zijn, zijn er enkele alternatieve methoden:

Meten: In sommige gevallen, vooral bij fysieke objecten, kun je de omtrek direct meten met een meetlint of een touwtje. Dit is echter niet altijd nauwkeurig, vooral bij grote of onregelmatige cirkels.
Online Rekenmachines: Er zijn talloze online rekenmachines beschikbaar die de omtrek van een cirkel kunnen berekenen als je de diameter of de straal invoert. Deze zijn handig voor snelle berekeningen, maar het is belangrijk om te begrijpen hoe de berekening werkt.

Conclusie

Het berekenen van de omtrek van een cirkel is een waardevolle vaardigheid die je in veel verschillende situaties kunt gebruiken. Met de eenvoudige formule en een beetje oefening kun je de omtrek van elke cirkel berekenen, van pizza's tot bloemperken. Onthoud dat wiskunde niet eng hoeft te zijn; het is gewoon een tool die je kunt gebruiken om de wereld om je heen beter te begrijpen.

Nu je de basisprincipes kent, ben je klaar om je wiskundige vaardigheden verder uit te breiden. Begin met het observeren van cirkelvormige objecten in je omgeving. Schat hun omtrek. Meet ze. Verifieer je schattingen met de formule. Door actief bezig te zijn met dit concept, zal je begrip en vertrouwen groeien.

Wat ga jij nu met deze nieuwe kennis doen? Zie je plotseling cirkels overal om je heen, en wil je ze allemaal opmeten?