Oppervlakte Cirkel Berekenen Met Diameter

Het berekenen van de oppervlakte van een cirkel is een fundamentele vaardigheid in de wiskunde, met talloze toepassingen in het dagelijks leven en in diverse vakgebieden. Hoewel de formule met de straal (r) misschien bekender is, is het net zo belangrijk om te begrijpen hoe je de oppervlakte kunt berekenen met behulp van de diameter (d). Dit artikel legt uit hoe je dit doet, met duidelijke uitleg en praktische voorbeelden.

Waarom de Diameter Gebruiken?

Vaak is de diameter van een cirkel makkelijker te meten dan de straal. Denk aan een rond object waar je makkelijk de afstand van de ene kant naar de andere kunt meten, maar moeilijk het exacte middelpunt kunt bepalen. In zulke gevallen is de diameter een handiger startpunt. Het is essentieel om flexibel te zijn in je aanpak en te kunnen kiezen welke gegevens je het beste kunt gebruiken.

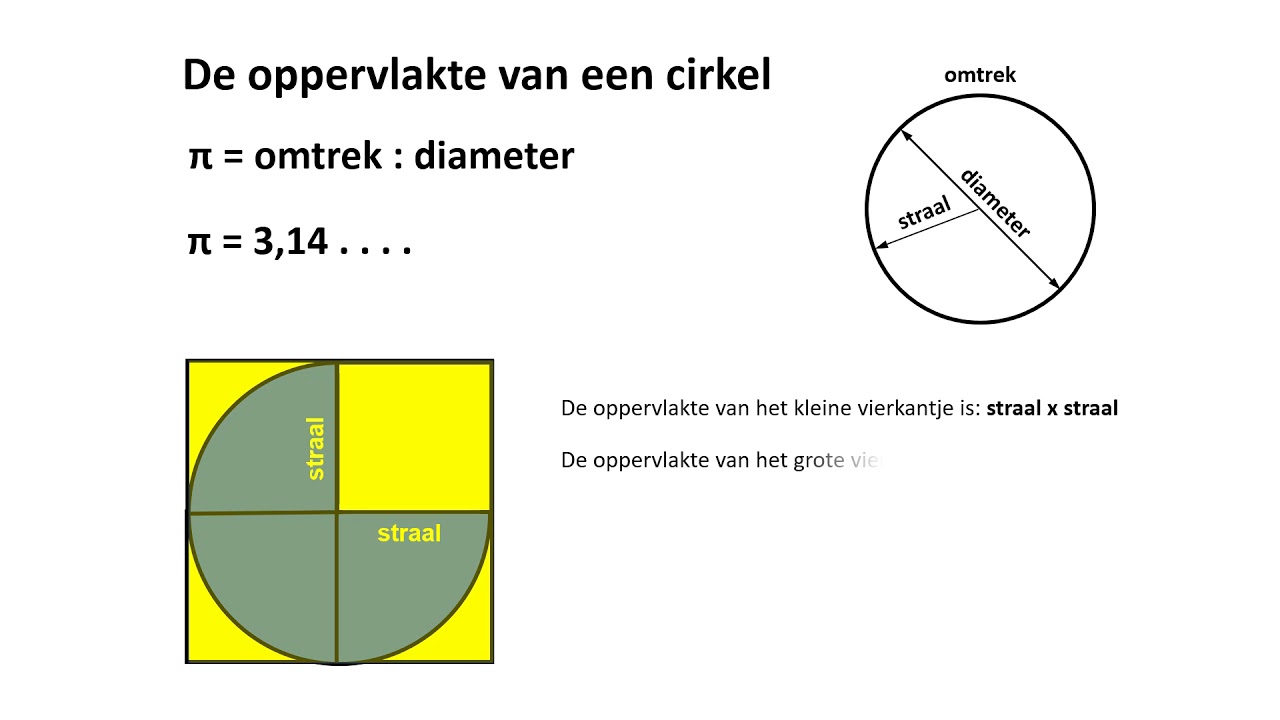
De Basis Relatie: Straal en Diameter

De relatie tussen de straal en de diameter is cruciaal: De diameter is altijd twee keer de straal. Dit wordt weergegeven door de formule: d = 2r. Omgekeerd is de straal de helft van de diameter: r = d/2. Deze eenvoudige relatie vormt de basis voor het berekenen van de oppervlakte met behulp van de diameter.

De Formule voor Oppervlakte met Diameter

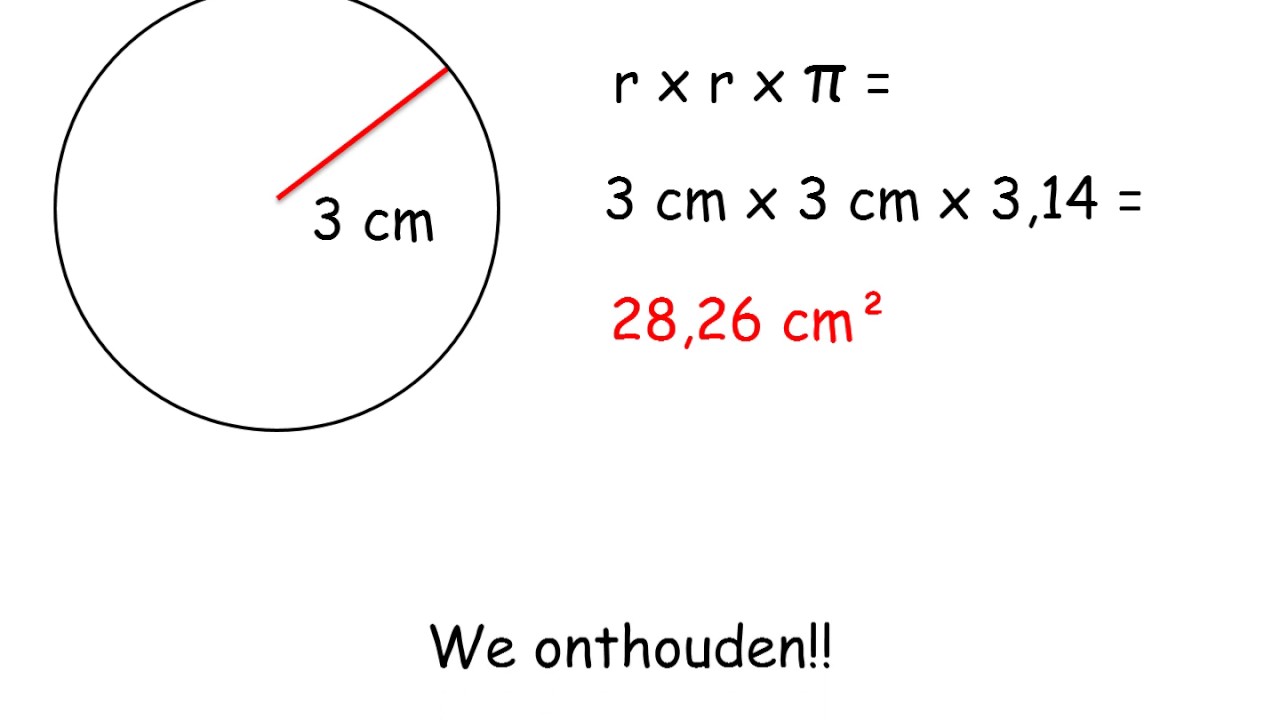
De bekende formule voor de oppervlakte (A) van een cirkel is: A = πr², waarbij π (pi) een wiskundige constante is met een waarde van ongeveer 3.14159. Om deze formule te gebruiken met de diameter, vervangen we 'r' door 'd/2'. Dit leidt tot de volgende formule:

A = π(d/2)²

Laten we deze formule vereenvoudigen:

A = π(d²/4)

Of, nog iets duidelijker:

A = (π/4)d²

Deze formule stelt ons in staat om de oppervlakte van een cirkel direct te berekenen, enkel en alleen met de diameter!

Stap-voor-Stap Berekening

Hier is een stapsgewijze handleiding voor het berekenen van de oppervlakte met de diameter:

1. Meet de diameter (d) van de cirkel. Zorg ervoor dat je de diameter nauwkeurig meet.
2. Kwadrateer de diameter (d²). Vermenigvuldig de diameter met zichzelf.
3. Vermenigvuldig het kwadraat met π (pi). Gebruik de waarde van π (ongeveer 3.14159).
4. Deel het resultaat door 4. Dit geeft je de oppervlakte van de cirkel.

Voorbeelden uit de Praktijk

Laten we een paar voorbeelden bekijken om de toepassing van deze formule te illustreren.

Voorbeeld 1: Een Pizzadeegroller

Stel, je hebt een pizzadeegroller met een diameter van 20 cm. Je wilt weten hoeveel oppervlakte je kunt bedekken met één rol. We gebruiken de formule:

A = (π/4)d²

A = (π/4) * 20²

A = (π/4) * 400

A ≈ 3.14159 / 4 * 400

A ≈ 0.7854 * 400

A ≈ 314.16 cm²

De pizzadeegroller kan dus ongeveer 314.16 vierkante centimeter deeg bedekken met één rol.

Voorbeeld 2: Een Vijver in de Tuin

Je bent een vijver aan het aanleggen en meet de diameter van de cirkelvormige uitsparing die je gegraven hebt. De diameter is 3 meter. Hoeveel folie heb je nodig om de vijver te bekleden?

Eerst zetten we meters om naar centimeters, dus 3 meter = 300 cm.

A = (π/4)d²

A = (π/4) * 300²

A = (π/4) * 90000

A ≈ 3.14159 / 4 * 90000

A ≈ 0.7854 * 90000

A ≈ 70686 cm²

Je hebt dus ongeveer 70686 vierkante centimeter folie nodig. Dit komt overeen met 7.0686 vierkante meter. Het is verstandig om iets meer folie te kopen om zeker te zijn dat je genoeg hebt voor de randen!

Voorbeeld 3: Berekening van een Boomstam

Een bosbouwer wil weten hoeveel hout er ongeveer in een boomstam zit. De diameter van de stam is op een bepaalde hoogte 50 cm. We nemen aan dat de stam over een kort stuk cilindervormig is en berekenen het oppervlak van de doorsnede. Dit kunnen we later gebruiken om het volume te schatten.

A = (π/4)d²

A = (π/4) * 50²

A = (π/4) * 2500

A ≈ 3.14159 / 4 * 2500

A ≈ 0.7854 * 2500

A ≈ 1963.5 cm²

De doorsnede van de boomstam is ongeveer 1963.5 vierkante centimeter.

Nauwkeurigheid en Afronding

De nauwkeurigheid van je resultaat hangt af van de nauwkeurigheid van je meting van de diameter en de waarde die je gebruikt voor π. In de praktijk is het vaak voldoende om π af te ronden tot 3.14. Bij zeer nauwkeurige berekeningen kun je een rekenmachine of software gebruiken die een meer precieze waarde van π hanteert. Het is belangrijk om je afronding te baseren op de benodigde precisie van je eindresultaat.

Wanneer Diameter de Voorkeur Heeft

Zoals eerder genoemd, heeft het gebruik van de diameter voordelen wanneer het direct meten van de straal lastig is. Dit kan het geval zijn bij:

• Objecten met een onduidelijk middelpunt: Denk aan het meten van een buis of een ring.
• Situaties waarbij direct meten sneller is: Het meten van een bestaande cirkelvormige structuur zonder toegang tot het middelpunt.
• Gegevens die al in diameter zijn gegeven: Sommige specificaties en technische tekeningen geven afmetingen in diameter.

Conclusie en Aanmoediging

Het berekenen van de oppervlakte van een cirkel met behulp van de diameter is een krachtige vaardigheid. Door de relatie tussen de straal en de diameter te begrijpen en de juiste formule toe te passen, kun je de oppervlakte eenvoudig en efficiënt berekenen, zelfs als je alleen de diameter kent. Deze kennis is nuttig in diverse situaties, van alledaagse problemen tot professionele toepassingen.

Oefen met verschillende voorbeelden om je vaardigheden te verbeteren. Probeer objecten in je omgeving te meten en hun oppervlakte te berekenen. Hoe meer je oefent, hoe zekerder je wordt in het toepassen van deze belangrijke wiskundige concepten. Succes!