Oppervlakte Van Een Cilinder Berekenen

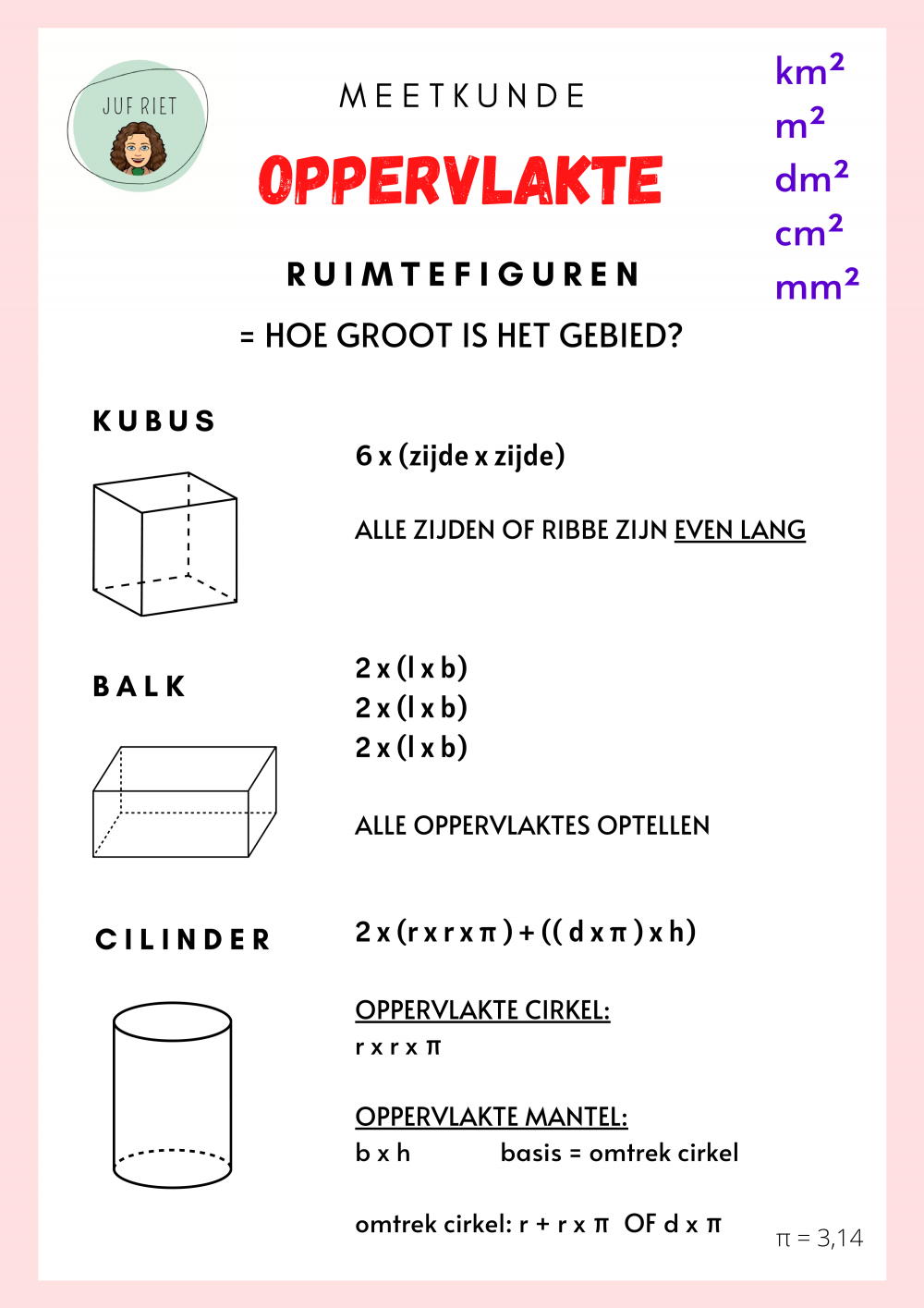
Het berekenen van de oppervlakte van een cilinder is een fundamentele vaardigheid in de wiskunde en heeft praktische toepassingen in diverse vakgebieden, van engineering tot dagelijks leven. In dit artikel gaan we dieper in op de formule, de stappen en de achterliggende principes om de oppervlakte van een cilinder nauwkeurig te bepalen.

Waarom de Oppervlakte van een Cilinder Berekenen?

Het begrijpen van de oppervlakte van een cilinder is cruciaal voor een aantal redenen:

Materialen schatten: Bij de fabricage van cilindervormige objecten, zoals tanks, pijpen of blikken, is het essentieel om de benodigde hoeveelheid materiaal te berekenen.
Warmteoverdracht: De oppervlakte speelt een cruciale rol bij het bepalen van de warmteoverdracht in warmtewisselaars en andere thermische systemen.
Architectuur en constructie: Het berekenen van de oppervlakte is essentieel bij het ontwerpen en bouwen van cilindervormige structuren, zoals kolommen en steunpilaren.
Volume-berekeningen: Hoewel dit artikel zich richt op oppervlakte, is het belangrijk te onthouden dat de oppervlakte essentieel is voor het begrijpen van het concept van volume en hoe je het volume van een cilinder kan berekenen.

Kortom, het is een basisconcept dat in veel verschillende gebieden van wetenschap en techniek terugkomt.

De Oppervlakteformule: Uitleg en Componenten

De totale oppervlakte (A) van een cilinder wordt berekend met de volgende formule:

A = 2πr² + 2πrh

Laten we de componenten van deze formule in detail bekijken:

Basisoppervlakte (2πr²)

Een cilinder heeft twee identieke cirkelvormige basisvlakken (de boven- en onderkant). De oppervlakte van een cirkel wordt berekend met de formule:

πr²

Waar:

π (pi) is een wiskundige constante, ongeveer gelijk aan 3,14159.
r is de straal van de cirkel (de afstand van het middelpunt tot de rand).

Omdat er twee cirkels zijn, vermenigvuldigen we de oppervlakte van één cirkel met 2: 2πr². Dit vertegenwoordigt de totale oppervlakte van de twee basisvlakken.

Manteloppervlakte (2πrh)

De manteloppervlakte is het gebogen oppervlak dat de twee basisvlakken verbindt. Je kunt je voorstellen dat je deze oppervlakte "openrolt" tot een rechthoek. De lengte van deze rechthoek is de omtrek van de cirkelvormige basis (2πr), en de breedte is de hoogte van de cilinder (h). Daarom is de oppervlakte van de mantel:

2πrh

Waar:

π (pi) is de wiskundige constante (≈ 3.14159).
r is de straal van de cirkel.
h is de hoogte van de cilinder (de afstand tussen de twee basisvlakken).

Totale Oppervlakte

Om de totale oppervlakte te berekenen, adderen we de oppervlakte van de twee basisvlakken en de manteloppervlakte:

A = 2πr² + 2πrh

Stapsgewijze Berekening: Een Praktisch Voorbeeld

Laten we een concreet voorbeeld bekijken om de berekening te illustreren. Stel dat we een cilinder hebben met:

Straal (r) = 5 cm
Hoogte (h) = 10 cm

Stap 1: Bereken de oppervlakte van de basisvlakken.

Oppervlakte van één basisvlak = πr² = π * (5 cm)² ≈ 3.14159 * 25 cm² ≈ 78.54 cm²

Oppervlakte van beide basisvlakken = 2 * 78.54 cm² ≈ 157.08 cm²

Stap 2: Bereken de manteloppervlakte.

Manteloppervlakte = 2πrh = 2 * π * 5 cm * 10 cm ≈ 2 * 3.14159 * 50 cm² ≈ 314.16 cm²

Stap 3: Bereken de totale oppervlakte.

Totale oppervlakte = Basisoppervlakte + Manteloppervlakte ≈ 157.08 cm² + 314.16 cm² ≈ 471.24 cm²

Dus de totale oppervlakte van de cilinder is ongeveer 471.24 cm².

Real-world voorbeelden en toepassingen

De berekening van de oppervlakte van een cilinder heeft talloze toepassingen in de echte wereld. Hier zijn enkele voorbeelden:

Blikjes: Bij het ontwerpen en produceren van blikjes (bijvoorbeeld voor soep, frisdrank, of verf) is het cruciaal om de oppervlakte van het blik te kennen om de hoeveelheid benodigd materiaal te minimaliseren en kosten te besparen. Een fabrikant kan berekenen hoeveel metaal er nodig is voor een blik van een bepaald formaat. Stel een fabriek produceert 1 miljoen blikjes per week. Een kleine reductie in het materiaal per blik kan leiden tot een enorme besparing op jaarbasis.
Pijpleidingen: Bij het construeren van pijpleidingen voor water, olie of gas is het van belang om de oppervlakte van de buizen te bepalen voor isolatie of coatings. Als een pijpleiding een diameter heeft van 1 meter en een lengte van 1 kilometer, dan kan de totale oppervlakte berekend worden om de hoeveelheid benodigde isolatie nauwkeurig te schatten.
Tanks: Het berekenen van de oppervlakte van tanks is belangrijk voor het bepalen van de hoeveelheid verf of coating die nodig is, en voor het berekenen van de warmteoverdracht in de tank. Denk aan een opslagtank voor water. De oppervlakte bepaalt hoeveel verf nodig is om de tank te beschermen tegen roest en corrosie.
Warmtewisselaars: De oppervlakte van de buizen in een warmtewisselaar is direct gerelateerd aan de efficiëntie van de warmteoverdracht. Een grotere oppervlakte betekent een betere warmteoverdracht. Ingenieurs gebruiken de formule om de optimale afmetingen van de warmtewisselaar te bepalen.
Architectuur: In architectuur kan de oppervlakte van cilindervormige kolommen gebruikt worden om de hoeveelheid benodigd materiaal voor de bekleding te bepalen.

Tips en aandachtspunten

Hier zijn enkele tips en aandachtspunten om in gedachten te houden bij het berekenen van de oppervlakte van een cilinder:

Consistentie van eenheden: Zorg ervoor dat alle metingen (straal en hoogte) in dezelfde eenheden zijn (bijvoorbeeld allemaal in centimeters of meters).
Gebruik een nauwkeurige waarde voor π: Hoewel 3.14 een acceptabele benadering is, kan het gebruik van een nauwkeuriger waarde van π (zoals de waarde op je rekenmachine) leiden tot preciezere resultaten, vooral bij grotere afmetingen.
Controleer je antwoord: Controleer altijd je antwoord om er zeker van te zijn dat het redelijk is in de context van het probleem. Een enorm groot getal voor de oppervlakte van een klein object is een indicatie van een fout.
Gebruik een rekenmachine: Voor complexe berekeningen kan een rekenmachine helpen om fouten te minimaliseren.
Vereenvoudiging: De formule kan ook vereenvoudigd worden tot A = 2πr (r+h). Dit kan handig zijn om de berekening sneller uit te voeren, maar zorg ervoor dat je de betekenis van elke term begrijpt.

Conclusie

Het berekenen van de oppervlakte van een cilinder is een belangrijke vaardigheid met talloze toepassingen in verschillende vakgebieden. Door de formule, de stappen en de achterliggende principes te begrijpen, kun je nauwkeurige berekeningen uitvoeren en problemen in de echte wereld oplossen. Oefening baart kunst. Probeer verschillende voorbeelden te berekenen om je vaardigheid te verbeteren. Begrijp de logica achter de formule, dan kan je het altijd toepassen!

We hopen dat dit artikel een duidelijke en begrijpelijke uitleg heeft gegeven over het berekenen van de oppervlakte van een cilinder. Blijf leren en ontdekken!