Oppervlakte Van Een Cirkel Berekenen

Ben je ooit gefascineerd geweest door de perfecte vorm van een cirkel? Van de wielen van een fiets tot de pizza die je vanavond gaat eten, cirkels zijn overal om ons heen. Maar heb je je ooit afgevraagd hoe je de oppervlakte van zo'n cirkel eigenlijk berekent? Geen zorgen! In dit artikel nemen we je mee op een heldere en begrijpelijke reis door de wereld van cirkels en hun oppervlakten. Of je nu een student bent die worstelt met wiskunde, een doe-het-zelver die een rond tafelblad wil maken, of gewoon iemand die nieuwsgierig is, hier leer je alles wat je moet weten.

Wat is een Cirkel Eigenlijk?

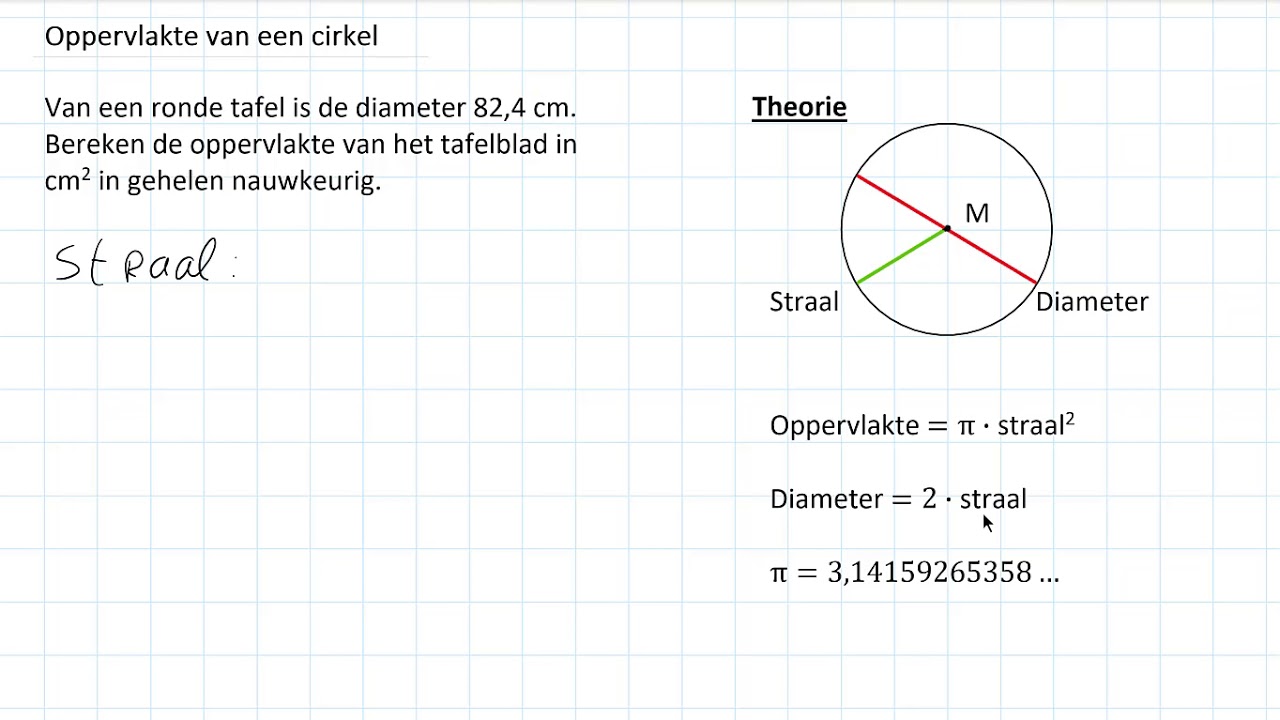
Laten we beginnen met de basis. Een cirkel is een perfect ronde vorm waarbij alle punten op de rand zich op dezelfde afstand van het middelpunt bevinden. Deze afstand van het middelpunt tot de rand noemen we de straal, vaak aangeduid met de letter r.

Belangrijke termen om te onthouden:

Straal (r): De afstand van het middelpunt tot de rand van de cirkel.
Diameter (d): De afstand van de ene kant van de cirkel naar de andere, door het middelpunt. De diameter is twee keer de straal (d = 2r).
Omtrek (O): De lengte van de rand van de cirkel.
Oppervlakte (A): De ruimte binnen de cirkel. Dit is wat we gaan berekenen.

De Magische Formule: A = πr²

De formule voor het berekenen van de oppervlakte van een cirkel is relatief eenvoudig: A = πr². Laten we deze formule even ontleden:

A staat voor de oppervlakte (area).
π (pi) is een speciale constante, een getal dat ongeveer gelijk is aan 3,14159. Pi is een irrationaal getal, wat betekent dat het oneindig veel decimalen heeft zonder een zich herhalend patroon. In de praktijk gebruiken we vaak 3,14 of de pi-knop op onze rekenmachine.
r staat voor de straal van de cirkel.
² (kwadraat) betekent dat we de straal met zichzelf vermenigvuldigen (r * r).

Dus, de formule zegt: om de oppervlakte van een cirkel te vinden, vermenigvuldig je pi met de straal in het kwadraat. Simpel, toch?

Stapsgewijs de Oppervlakte Berekenen

Laten we de formule in actie zien met een paar voorbeelden. We gaan stapsgewijs de oppervlakte berekenen:

Voorbeeld 1: Straal is Bekend

Stel, we hebben een cirkel met een straal van 5 cm. Hoe berekenen we de oppervlakte?

Schrijf de formule op: A = πr²
Vervang de straal: A = π * 5²
Bereken de straal in het kwadraat: A = π * 25
Vermenigvuldig met pi: A ≈ 3,14 * 25
Bereken de oppervlakte: A ≈ 78,5 cm²

De oppervlakte van de cirkel is dus ongeveer 78,5 vierkante centimeter. Vergeet niet de eenheid! Omdat de straal in centimeters was, is de oppervlakte in vierkante centimeters.

Voorbeeld 2: Diameter is Bekend

Wat als we de diameter van een cirkel weten in plaats van de straal? Geen probleem! We weten dat de diameter twee keer de straal is (d = 2r). Dus, om de straal te vinden, delen we de diameter door 2 (r = d/2).

Stel, we hebben een cirkel met een diameter van 10 meter. Hoe berekenen we de oppervlakte?

Bereken de straal: r = d/2 = 10/2 = 5 meter
Schrijf de formule op: A = πr²
Vervang de straal: A = π * 5²
Bereken de straal in het kwadraat: A = π * 25
Vermenigvuldig met pi: A ≈ 3,14 * 25
Bereken de oppervlakte: A ≈ 78,5 m²

De oppervlakte van de cirkel is dus ongeveer 78,5 vierkante meter.

Waarom is dit Belangrijk? Praktische Toepassingen

Het berekenen van de oppervlakte van een cirkel is veel meer dan alleen een wiskundige oefening. Het heeft talloze praktische toepassingen in het dagelijks leven en in verschillende vakgebieden. Hier zijn een paar voorbeelden:

Bouwkunde: Architecten en ingenieurs gebruiken de formule om de benodigde materialen voor ronde structuren te berekenen, zoals koepels, zwembaden en vijvers.
Landbouw: Boeren kunnen de oppervlakte van ronde velden berekenen om de hoeveelheid zaaigoed, meststoffen en water te bepalen die nodig is.
Koken: Koks gebruiken de formule om de grootte van taartvormen te bepalen en de juiste hoeveelheid beslag te bereiden.
Techniek: Ingenieurs gebruiken de formule bij het ontwerpen van machines en onderdelen, zoals wielen, tandwielen en lagers.
Doe-het-zelven: Je kunt het gebruiken om de hoeveelheid verf te berekenen die nodig is voor een ronde tafel, de hoeveelheid stof voor een cirkelvormig kussen, of de grootte van een rond terras.

Tips en Trucs voor Succes

Hier zijn een paar tips om het berekenen van de oppervlakte van een cirkel nog makkelijker te maken:

Gebruik een rekenmachine: Een rekenmachine met een pi-knop geeft je een nauwkeuriger resultaat dan het gebruik van 3,14.
Let op de eenheden: Zorg ervoor dat je de juiste eenheden gebruikt en dat je ze consistent houdt. Als de straal in centimeters is, is de oppervlakte in vierkante centimeters.
Controleer je antwoord: Maak een schatting van de oppervlakte om te controleren of je antwoord redelijk is. Als de straal 10 is, weet je dat de oppervlakte ongeveer 300 (3 * 10²) moet zijn.
Oefening baart kunst: Hoe meer je oefent, hoe sneller en zelfverzekerder je wordt.
Online hulpmiddelen: Er zijn veel online calculators die je kunnen helpen bij het berekenen van de oppervlakte van een cirkel. Ze zijn handig om je antwoorden te controleren of om snel een berekening uit te voeren.

Veelgemaakte Fouten en Hoe Ze te Vermijden

Hier zijn enkele veelgemaakte fouten die mensen maken bij het berekenen van de oppervlakte van een cirkel:

De straal en diameter verwarren: Zorg ervoor dat je de straal (r) gebruikt en niet de diameter (d). Vergeet niet dat r = d/2.
Vergeten om de straal te kwadrateren: De formule is A = πr², dus je moet de straal met zichzelf vermenigvuldigen (r * r).
De verkeerde waarde voor pi gebruiken: Gebruik 3,14 of de pi-knop op je rekenmachine voor een nauwkeuriger resultaat.
De eenheden vergeten: Vergeet niet om de juiste eenheden te vermelden (bijv. cm², m², enz.).

De Kracht van Pi

Pi (π) is een fascinerend getal dat in veel gebieden van de wiskunde en natuurkunde voorkomt. Het is een transcendentaal getal, wat betekent dat het geen wortel is van een polynoomvergelijking met rationale coëfficiënten. Dit maakt het een van de meest intrigerende en bestudeerde getallen in de wiskundige geschiedenis. De benadering van Pi tot op vele duizenden decimalen is al jaren een hobby van wiskundigen en computerwetenschappers.

Conclusie: Beheers de Cirkel, Beheers de Wereld (Nou ja, Bijna...)

Het berekenen van de oppervlakte van een cirkel is een fundamentele vaardigheid met veel praktische toepassingen. Door de formule (A = πr²) te begrijpen en te oefenen met verschillende voorbeelden, kun je zelfverzekerd en nauwkeurig de oppervlakte van elke cirkel berekenen. Of je nu een student bent, een professional, of gewoon iemand die geïnteresseerd is in wiskunde, deze kennis zal je zeker van pas komen. Dus ga erop uit en omarm de cirkel! Je zult verbaasd zijn hoe vaak je deze vaardigheid zult gebruiken. En wie weet, misschien inspireert het je zelfs om de fascinerende wereld van de wiskunde verder te verkennen.

We hopen dat dit artikel je heeft geholpen om de oppervlakte van een cirkel beter te begrijpen. Blijf oefenen, blijf leren en blijf nieuwsgierig!