Oppervlakte Van Een Cirkel Formule

Heb je ooit naar een perfect ronde pizza gekeken en je afgevraagd hoeveel pepperoni je erop zou kunnen leggen? Of misschien moest je berekenen hoeveel verf je nodig had om een rond tuinprieel te schilderen? In beide gevallen heb je de oppervlakte van een cirkel nodig! Het klinkt misschien ingewikkeld, maar geloof me, met de juiste uitleg is het eigenlijk heel eenvoudig.

Veel mensen vinden wiskunde ingewikkeld, vooral formules. Maar in dit geval ga ik je laten zien dat de formule voor de oppervlakte van een cirkel verrassend eenvoudig en enorm nuttig is in het dagelijks leven. Laten we er samen induiken!

Wat is een Cirkel en wat is Oppervlakte eigenlijk?

Laten we beginnen met de basis. Een cirkel is een perfect ronde figuur, waarbij alle punten op de rand dezelfde afstand hebben tot het middelpunt. Denk aan een wiel, een munt, of een bloem. De afstand van het middelpunt tot de rand noemen we de radius (straal).

Oppervlakte, daarentegen, is de hoeveelheid ruimte die een tweedimensionale vorm beslaat. Simpel gezegd: het is de hoeveelheid 'vlak' die binnen de omtrek van de cirkel ligt. Denk aan de hoeveelheid gras in een rond grasveld, of de hoeveelheid stof die je nodig hebt om een ronde tafel te bedekken.

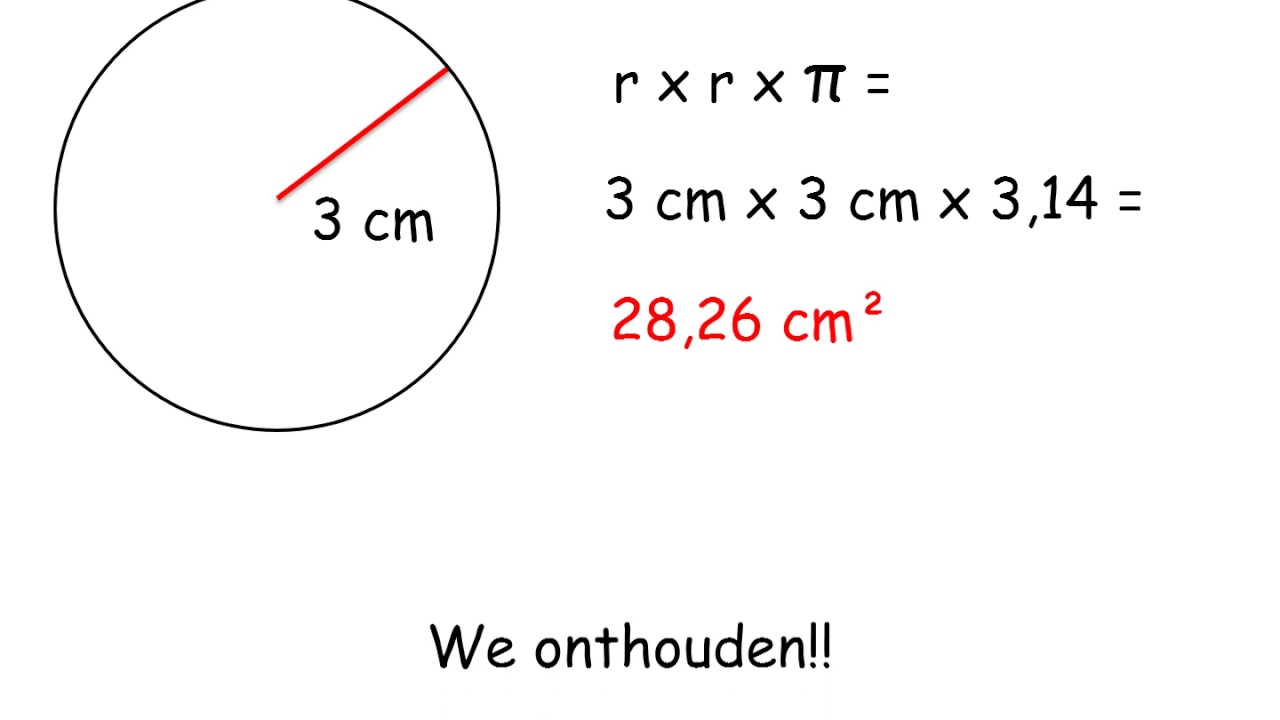
De Magische Formule: A = πr²

De formule voor de oppervlakte van een cirkel is: A = πr²

Laten we die formule even ontleden:

• A staat voor de oppervlakte van de cirkel. Dit is wat we willen berekenen!
• π (Pi) is een speciale constante die ongeveer gelijk is aan 3.14159. Het is een irrationeel getal, wat betekent dat het oneindig veel decimalen heeft zonder een herhalend patroon. Voor de meeste berekeningen gebruiken we 3.14 als een goede benadering.
• r staat voor de radius van de cirkel, zoals we eerder besproken hebben.
• ² betekent "in het kwadraat", wat inhoudt dat je de radius met zichzelf moet vermenigvuldigen (r * r).

Dus, om de oppervlakte van een cirkel te berekenen, vermenigvuldig je Pi (π) met het kwadraat van de radius (r²). Simpel, toch?

Hoe Gebruik je de Formule in de Praktijk?

Laten we een paar voorbeelden bekijken om de formule in actie te zien:

Voorbeeld 1: De Pizza

Stel je voor dat je een pizza hebt met een diameter van 30 cm. Om de radius te vinden, deel je de diameter door 2: 30 cm / 2 = 15 cm. De radius (r) is dus 15 cm.

Nu kunnen we de formule toepassen: A = πr²

A = 3.14 * 15²

A = 3.14 * 225

A = 706.5 cm²

De oppervlakte van de pizza is ongeveer 706.5 vierkante centimeter. Dat is veel pizza!

Voorbeeld 2: Het Ronde Tapijt

Je wilt een rond tapijt kopen voor je woonkamer. Het tapijt heeft een radius van 2 meter. Hoeveel vloeroppervlak zal het tapijt bedekken?

A = πr²

A = 3.14 * 2²

A = 3.14 * 4

A = 12.56 m²

Het tapijt zal ongeveer 12.56 vierkante meter vloeroppervlak bedekken.

Voorbeeld 3: De Tuin Vijver

Je bent van plan een ronde vijver in je tuin aan te leggen. De vijver zal een radius van 1.5 meter hebben. Hoeveel water heb je nodig om de vijver te vullen (uitgaande van een uniforme diepte)? Dit is eigenlijk een berekening van volume, maar de oppervlakte is de eerste stap!

A = πr²

A = 3.14 * 1.5²

A = 3.14 * 2.25

A = 7.065 m²

De oppervlakte van de vijver is 7.065 vierkante meter. Nu je de oppervlakte weet, kun je met de diepte de hoeveelheid water berekenen die je nodig hebt.

Waarom is dit Belangrijk?

De formule voor de oppervlakte van een cirkel is niet alleen nuttig voor het oplossen van wiskundige problemen. Het komt in allerlei dagelijkse situaties van pas:

• Architectuur en Bouw: Het berekenen van de oppervlakte van ronde ramen, koepels, of funderingen.
• Engineering: Het ontwerpen van ronde onderdelen voor machines en voertuigen.
• Tuinieren: Het bepalen van de hoeveelheid zaad of gras nodig voor een rond gazon.
• Koken: Zoals we al zagen, voor het berekenen van de hoeveelheid ingrediënten die nodig zijn voor een ronde taart of pizza.
• Fabricage: Het bepalen van de hoeveelheid materiaal die nodig is om ronde objecten te produceren.

Zoals je ziet, is de formule van de oppervlakte van een cirkel een fundamentele wiskundige tool met veel praktische toepassingen.

Tips en Trucs voor het Gebruik van de Formule

Hier zijn een paar handige tips om het berekenen van de oppervlakte van een cirkel nog makkelijker te maken:

• Wees nauwkeurig: Gebruik een nauwkeurige waarde voor Pi (π) als je een heel precies resultaat nodig hebt. De meeste rekenmachines hebben een Pi-knop die een meer accurate waarde geeft dan 3.14.
• Gebruik de juiste eenheden: Zorg ervoor dat je de juiste eenheden gebruikt voor de radius. Als de radius in centimeters is, zal de oppervlakte in vierkante centimeters zijn. Als de radius in meters is, zal de oppervlakte in vierkante meters zijn.
• Diameter versus Radius: Onthoud dat de radius de helft is van de diameter. Als je de diameter krijgt, deel deze dan door 2 om de radius te vinden.
• Rekenmachines en Online Tools: Er zijn veel online rekenmachines beschikbaar die je kunt gebruiken om de oppervlakte van een cirkel te berekenen. Dit kan handig zijn als je geen rekenmachine bij de hand hebt, of als je complexe berekeningen wilt uitvoeren.
• Oefening Baart Kunst: Hoe meer je oefent met het gebruiken van de formule, hoe vertrouwder je ermee wordt. Probeer verschillende voorbeelden te berekenen om je vaardigheden te verbeteren.

Verder dan de Basis: Complexere Toepassingen

Hoewel de basisformule simpel is, kan de oppervlakte van een cirkel ook gebruikt worden in complexere problemen. Denk bijvoorbeeld aan:

• Oppervlakte van een Cirkelsegment: Een segment is het gebied dat wordt afgesneden van een cirkel door een lijn (een koorde). De berekening hiervan is complexer, en vereist trigonometrie.
• Oppervlakte van een Cirkelsector: Een sector is het gebied tussen twee radii en de boog die ze verbinden. Ook hierbij is extra kennis nodig, hoewel het principe hetzelfde blijft.
• Gecombineerde Vormen: Je kunt de oppervlakte van een cirkel combineren met de oppervlakte van andere vormen (zoals vierkanten of rechthoeken) om de oppervlakte van complexe figuren te berekenen.

Deze complexere toepassingen vereisen meer geavanceerde wiskundige kennis, maar de basisformule A = πr² blijft de fundamentele bouwsteen.

Conclusie: De Oppervlakte van een Cirkel is Machtig!

Hopelijk heb je nu een goed begrip van de formule voor de oppervlakte van een cirkel en hoe je deze in verschillende situaties kunt toepassen. Onthoud: A = πr². Het is een krachtige formule die je kan helpen bij het oplossen van een breed scala aan problemen, van alledaagse situaties tot complexe technische uitdagingen.

Dus de volgende keer dat je een perfect ronde vorm ziet, denk dan aan deze formule en realiseer je hoe nuttig wiskunde kan zijn! En vergeet niet: oefening baart kunst. Blijf oefenen en je zult een meester worden in het berekenen van de oppervlakte van cirkels!

Of je nu een pizza snijdt, een tuin ontwerpt, of een machine bouwt, de oppervlakte van een cirkel is een concept dat je leven makkelijker kan maken. Dus ga erop uit en omarm de cirkel!