Piramide Met 4 Gelijkzijdige Driehoeken

Een object dat fascineert en inspireert over de hele wereld, de piramide. Wanneer mensen aan piramides denken, stellen ze zich vaak de massieve bouwwerken van het oude Egypte voor. Maar de term "piramide" verwijst naar een veel bredere categorie geometrische vormen. Een bijzonder interessante variant is de piramide met vier gelijkzijdige driehoeken, ook wel bekend als een regelmatig viervlak of tetraëder. In dit artikel duiken we dieper in de eigenschappen, toepassingen en betekenis van deze intrigerende vorm.

Wat is een Regelmatig Viervlak?

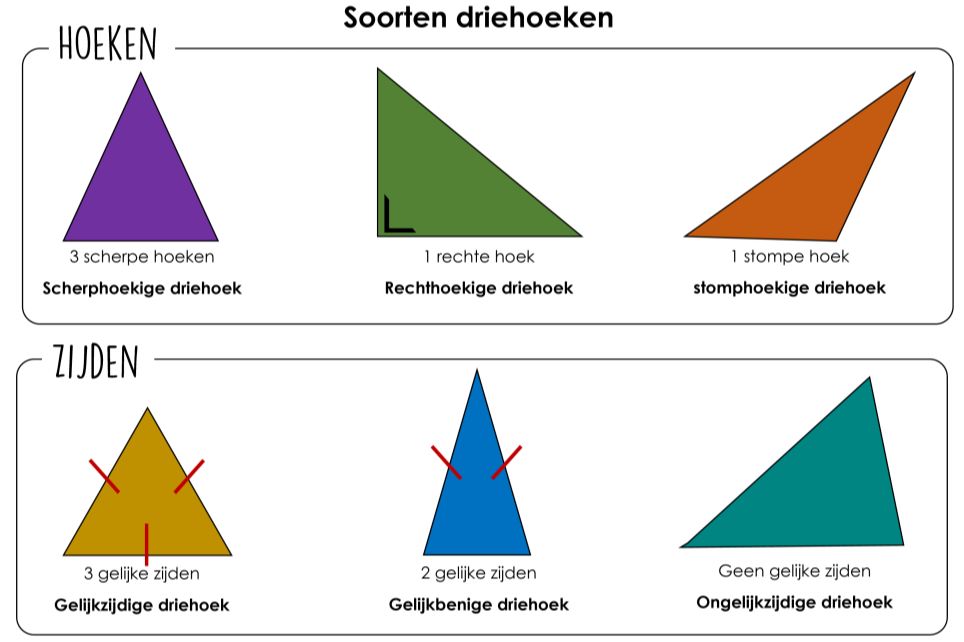
Een regelmatig viervlak, of tetraëder, is een driedimensionale vorm die wordt begrensd door vier gelijkzijdige driehoeken. Dit betekent dat alle vier de zijvlakken identiek zijn en alle ribben dezelfde lengte hebben. Het is een van de vijf platonische lichamen, die worden gekenmerkt door hun regelmatige en symmetrische structuur.

Kenmerken en Eigenschappen

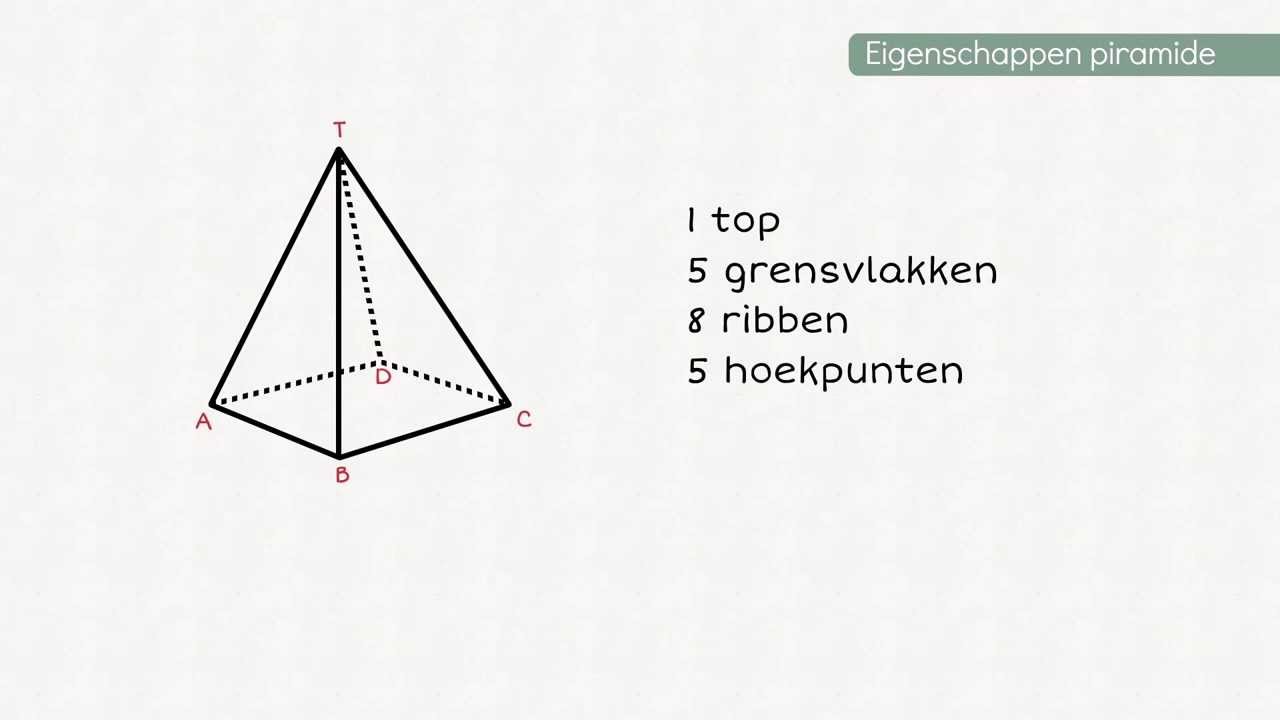
Het regelmatig viervlak heeft een aantal opvallende kenmerken:

• Aantal vlakken: 4 (allemaal gelijkzijdige driehoeken)
• Aantal hoekpunten: 4
• Aantal ribben: 6
• Elke hoekpunt is de samenkomst van: 3 ribben en 3 vlakken
• Zwaartepunt: Het zwaartepunt bevindt zich in het midden van het viervlak.
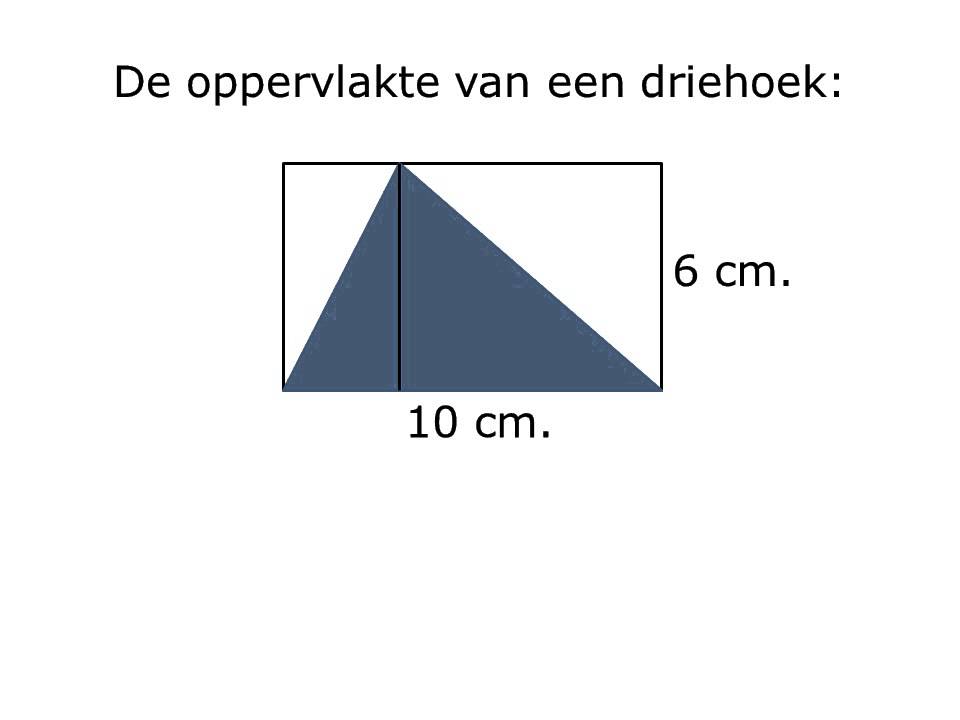
• Oppervlakte: De totale oppervlakte van een regelmatig viervlak met ribbe 'a' is √3 * a².
• Volume: Het volume van een regelmatig viervlak met ribbe 'a' is (a³ * √2) / 12.

Een van de meest intrigerende eigenschappen van een regelmatig viervlak is de symmetrie. Omdat alle zijden en hoeken gelijk zijn, bezit het een hoge mate van rotatie- en spiegelingssymmetrie. Dit maakt het tot een visueel aantrekkelijke en harmonieuze vorm.

De Wiskunde Achter het Viervlak

De geometrie van het regelmatig viervlak is rijk en complex, en het vormt de basis voor veel wiskundige concepten. Het kan bijvoorbeeld worden gebruikt om concepten zoals vectoralgebra, matrices en transformaties te illustreren.

Afstand tot een vlak

Een interessante wiskundige uitdaging is het berekenen van de afstand van een hoekpunt tot het tegenoverliggende vlak in een regelmatig viervlak. Deze afstand, ook wel de hoogte genoemd, kan worden berekend met behulp van de stelling van Pythagoras en elementaire trigonometrie. De formule voor de hoogte (h) is: h = (√(2/3)) * a, waarbij 'a' de lengte van de ribbe is.

Dihedrale Hoek

De dihedrale hoek is de hoek tussen twee aangrenzende vlakken van het viervlak. Voor een regelmatig viervlak is deze hoek arccos(1/3), wat ongeveer 70.53 graden is. Het is een constante waarde, wat de regelmaat van deze vorm benadrukt.

Toepassingen van het Viervlak in de Wereld

Het regelmatig viervlak is niet alleen een abstract wiskundig concept, maar heeft ook tal van praktische toepassingen in verschillende disciplines.

Chemie en Moleculaire Structuur

In de chemie is het viervlak een belangrijke structuur voor het begrijpen van de ruimtelijke ordening van moleculen. Het meest bekende voorbeeld is het methaanmolecuul (CH4). Het koolstofatoom in methaan bevindt zich in het centrum van een viervlak, met de vier waterstofatomen op de hoekpunten. Deze tetraëdrische geometrie minimaliseert de afstoting tussen de waterstofatomen en zorgt voor een stabiele moleculaire structuur. Dit principe strekt zich uit tot vele andere organische en anorganische moleculen, waarbij de tetraëdrische coördinatie een sleutelrol speelt in hun reactiviteit en eigenschappen.

Daarnaast spelen tetraëdrische eenheden een belangrijke rol in de structuur van sommige kristalroosters, bijvoorbeeld in silicaten, de meest voorkomende mineralen in de aardkorst. De SiO4 tetraëder is de fundamentele bouwsteen van deze materialen, en de manier waarop deze tetraëders met elkaar verbonden zijn, bepaalt de eigenschappen van het mineraal.

Architectuur en Design

Hoewel minder frequent dan kubussen of rechthoeken, zijn viervlakken ook in architectuur en design te vinden. Ze kunnen gebruikt worden als basisvorm voor koepels, daken en andere structurele elementen. Een bekend voorbeeld is de "Eden Project" in Cornwall, Engeland, waar grote geodetische koepels, bestaande uit een netwerk van driehoeken, een viervlakachtige structuur vertonen. De stevigheid en efficiëntie van de driehoekige vorm maken ze aantrekkelijk voor het construeren van grote overspanningen met relatief weinig materiaal.

In de kunst en design wordt het viervlak vaak gebruikt als een esthetisch element. De eenvoudige en symmetrische vorm spreekt tot de verbeelding en kan gebruikt worden om een gevoel van balans en harmonie te creëren. Sieraden, sculpturen en zelfs meubels kunnen gebaseerd zijn op de vorm van het viervlak.

Spelletjes en Recreatie

Het viervlak komt ook voor in verschillende spelletjes en recreatieve activiteiten. Een bekend voorbeeld is de D4 dobbelsteen, een vierzijdige dobbelsteen die gebruikt wordt in rollenspellen zoals Dungeons & Dragons. De relatieve eenvoud van de vorm maakt het makkelijk te produceren en te gooien.

Ook in puzzels komt het viervlak voor. Er zijn bijvoorbeeld puzzels waarbij men een grotere vorm moet construeren uit kleinere viervlakken, of waarbij men een viervlak moet vouwen uit een plat patroon. Deze puzzels zijn een leuke manier om ruimtelijk inzicht en probleemoplossende vaardigheden te trainen.

Wiskunde en Onderwijs

Het regelmatig viervlak is een uitstekend hulpmiddel voor het onderwijzen van geometrie en ruimtelijk inzicht. Het is een concrete vorm die leerlingen kunnen manipuleren en onderzoeken, waardoor ze een beter begrip krijgen van concepten zoals vlakken, ribben, hoekpunten, oppervlakte en volume. Door het viervlak te bestuderen, kunnen leerlingen ook kennismaken met de principes van symmetrie en platonische lichamen.

Het kan gebruikt worden om wiskundige principes zoals de stelling van Pythagoras, trigonometrie en vectoralgebra te illustreren. Het is een visueel aantrekkelijke en concrete manier om abstracte concepten te introduceren, waardoor het leren boeiender en effectiever wordt.

Beperkingen en Uitdagingen

Hoewel het viervlak vele voordelen biedt, zijn er ook enkele beperkingen en uitdagingen verbonden aan het gebruik ervan.

Een van de grootste uitdagingen is de instabiliteit. In vergelijking met bijvoorbeeld een kubus is een viervlak relatief instabiel. Het kan makkelijk omvallen, waardoor het minder geschikt is voor bepaalde toepassingen. In de architectuur moet hier rekening mee gehouden worden door het viervlak te combineren met andere structurele elementen om de stabiliteit te vergroten.

Daarnaast is het volume-oppervlakte ratio van een viervlak relatief laag in vergelijking met andere vormen. Dit betekent dat het minder efficiënt is in het opslaan van volume in verhouding tot het oppervlak. Dit kan een nadeel zijn in toepassingen waarbij het maximaliseren van het volume belangrijk is.

Conclusie

Het regelmatig viervlak, of de piramide met vier gelijkzijdige driehoeken, is meer dan alleen een eenvoudige geometrische vorm. Het is een bron van fascinatie, een bouwsteen van de natuur en een hulpmiddel voor het begrijpen van de wereld om ons heen. Van de moleculaire structuur van methaan tot de architectuur van geodetische koepels, het viervlak is een veelzijdige en invloedrijke vorm. Door de eigenschappen, toepassingen en betekenis van het viervlak te begrijpen, kunnen we onze waardering voor wiskunde, wetenschap en kunst verdiepen.

Daag jezelf uit! Zoek naar viervlakken in je omgeving. Denk na over hoe deze vorm gebruikt wordt en welke voordelen hij biedt. Of probeer zelf een viervlak te construeren uit papier of andere materialen. Het verkennen van de wereld door de lens van het viervlak kan een verrassend lonende ervaring zijn. Ontdek de schoonheid en de kracht van deze fundamentele vorm!