Schaal Berekenen Groep 8 Werkblad

Schaalberekening is een essentieel onderdeel van de wiskundelessen in groep 8. Het helpt kinderen de verhoudingen tussen afstanden op een kaart of plattegrond en de werkelijke afstanden in de echte wereld te begrijpen. Dit is niet alleen een abstracte wiskundige oefening, maar een vaardigheid die in vele dagelijkse situaties van pas komt. Een werkblad over schaalberekening in groep 8 is een krachtig hulpmiddel om deze concepten te verduidelijken en kinderen te helpen de vaardigheden te ontwikkelen die ze nodig hebben om schaal effectief te gebruiken.

Waarom is Schaalberekening Belangrijk?

Schaalberekening is meer dan alleen een wiskundige truc. Het is een fundamentele vaardigheid die studenten helpt de wereld om hen heen te begrijpen. Hier zijn enkele redenen waarom schaalberekening zo belangrijk is:

Ruimtelijk Inzicht

Schaalberekening draagt bij aan het ontwikkelen van ruimtelijk inzicht. Kinderen leren hoe ze een tweedimensionale weergave (zoals een kaart) kunnen gebruiken om een driedimensionale ruimte te begrijpen. Dit helpt hen bij het visualiseren van afstanden en het begrijpen van de relaties tussen verschillende locaties.

Praktische Toepassingen

Schaalberekening heeft veel praktische toepassingen. Denk aan het plannen van een reis met behulp van een kaart, het lezen van bouwtekeningen, of het begrijpen van de verhoudingen in een modelbouwproject. Zonder begrip van schaal zouden deze taken veel moeilijker, zo niet onmogelijk, zijn.

Logisch Redeneren

Het werken met schalen vereist logisch redeneren en probleemoplossend vermogen. Kinderen leren hoe ze verhoudingen kunnen interpreteren, proporties kunnen berekenen en de juiste formules kunnen toepassen om problemen op te lossen. Dit zijn waardevolle vaardigheden die hen in andere vakken en in het latere leven van pas zullen komen.

Voorbereiding op Voortgezet Onderwijs

Een goede basis in schaalberekening is cruciaal voor voortgezet onderwijs, met name in vakken als aardrijkskunde, wiskunde en natuurkunde. Begrip van schaal is essentieel voor het interpreteren van kaarten, diagrammen en modellen die in deze vakken worden gebruikt.

Hoe Werkt Schaalberekening?

De basis van schaalberekening ligt in het begrijpen van verhoudingen. Een schaal wordt meestal weergegeven als een verhouding, bijvoorbeeld 1:100. Dit betekent dat 1 cm op de kaart overeenkomt met 100 cm (of 1 meter) in de werkelijkheid.

Om een afstand op een kaart om te zetten naar de werkelijke afstand, moet je de afstand op de kaart vermenigvuldigen met de schaalfactor. Omgekeerd, om een werkelijke afstand om te zetten naar een afstand op de kaart, moet je de werkelijke afstand delen door de schaalfactor.

Voorbeeld 1: Afstand Berekenen op een Kaart

Stel, de schaal van een kaart is 1:50.000 en de afstand tussen twee steden op de kaart is 8 cm. Wat is de werkelijke afstand tussen de twee steden?

Oplossing:

De schaalfactor is 50.000.
De afstand op de kaart is 8 cm.
De werkelijke afstand is 8 cm * 50.000 = 400.000 cm.
Om dit om te zetten naar kilometers: 400.000 cm = 4.000 meter = 4 kilometer.

De werkelijke afstand tussen de twee steden is dus 4 kilometer.

Voorbeeld 2: Afstand Berekenen in Werkelijkheid

Stel, de schaal van een plattegrond is 1:200 en de werkelijke lengte van een kamer is 6 meter. Hoe lang is de kamer op de plattegrond?

Oplossing:

De schaalfactor is 200.
De werkelijke lengte is 6 meter = 600 cm.
De lengte op de plattegrond is 600 cm / 200 = 3 cm.

De lengte van de kamer op de plattegrond is dus 3 cm.

Schaal Berekenen Groep 8 Werkblad: Een Praktische Benadering

Een goed ontworpen werkblad voor schaalberekening in groep 8 moet verschillende elementen bevatten om het leren effectief en boeiend te maken. Hier zijn enkele belangrijke onderdelen:

Verschillende Soorten Opgaven

Het werkblad moet een verscheidenheid aan opgaven bevatten om verschillende aspecten van schaalberekening te oefenen. Dit kunnen opgaven zijn waarin kinderen afstanden op een kaart moeten meten en omrekenen, opgaven waarin ze afstanden in de werkelijkheid moeten omrekenen naar de kaart, en opgaven waarin ze de schaal zelf moeten berekenen.

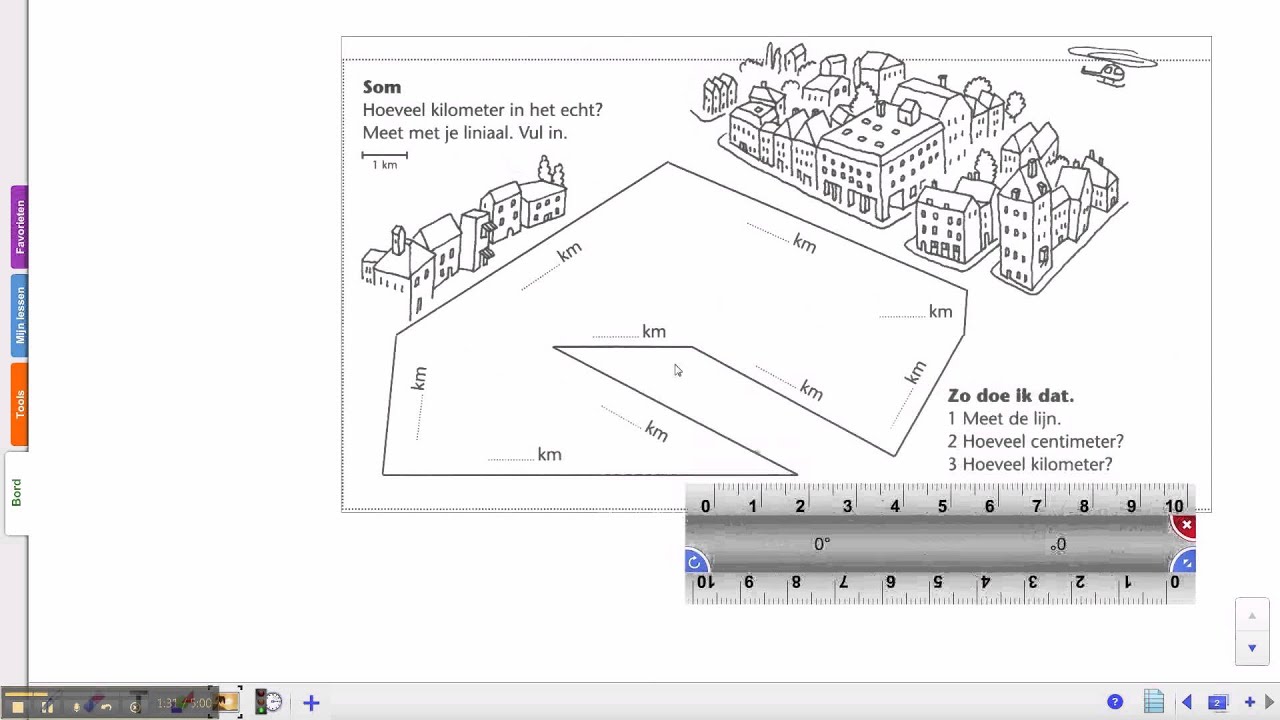
Visuele Ondersteuning

Visuele ondersteuning is cruciaal voor het begrijpen van schaal. Het werkblad kan kaarten, plattegronden en andere visuele hulpmiddelen bevatten om de opgaven te illustreren en de leerlingen te helpen de relatie tussen de kaart en de werkelijkheid te visualiseren.

Realistische Scenario's

Het gebruik van realistische scenario's maakt de opgaven relevanter en boeiender. Denk aan opgaven die te maken hebben met het plannen van een vakantie, het ontwerpen van een tuin, of het bouwen van een model. Dit helpt de kinderen te zien hoe schaalberekening in de praktijk wordt gebruikt.

Stapsgewijze Uitleg

Het werkblad moet stapsgewijze uitleg en voorbeelden bevatten om de leerlingen te helpen de concepten te begrijpen. Dit is vooral belangrijk voor leerlingen die moeite hebben met schaalberekening. Door duidelijke uitleg en voorbeelden kunnen ze de opgaven zelfstandig aanpakken.

Differentiatie

Een goed werkblad biedt mogelijkheden voor differentiatie. Dit betekent dat er opgaven van verschillende niveaus zijn, zodat zowel sterke als zwakkere leerlingen aan hun eigen niveau kunnen werken. Dit kan door opgaven te variëren in moeilijkheidsgraad, complexiteit en context.

Voorbeelden van Real-World Toepassingen

Om het belang van schaalberekening te benadrukken, is het nuttig om voorbeelden van real-world toepassingen te geven:

Reizen: Het plannen van een route met behulp van een kaart en het berekenen van de afstanden tussen verschillende locaties.
Architectuur: Het lezen en begrijpen van bouwtekeningen en plattegronden.
Modelbouw: Het bouwen van modellen op schaal, zoals modeltreinen, modelauto's en modelvliegtuigen.
Cartografie: Het maken en interpreteren van kaarten, inclusief topografische kaarten en thematische kaarten.
Tuinieren: Het ontwerpen van een tuin en het bepalen van de afmetingen van plantenbedden en paden.

Een concreet voorbeeld: Stel, een leerling wil een model van zijn slaapkamer maken. De werkelijke lengte van de kamer is 4 meter en de breedte is 3 meter. De leerling besluit een schaal van 1:20 te gebruiken. Dit betekent dat 1 cm op het model overeenkomt met 20 cm in de werkelijkheid. De lengte van de kamer op het model is dan 400 cm / 20 = 20 cm en de breedte is 300 cm / 20 = 15 cm. De leerling kan nu een model van zijn kamer maken met de juiste verhoudingen.

Conclusie en Call to Action

Schaalberekening is een essentiële vaardigheid die leerlingen in groep 8 helpt de wereld om hen heen te begrijpen en zich voor te bereiden op het voortgezet onderwijs. Een goed ontworpen werkblad kan een krachtig hulpmiddel zijn om deze concepten te verduidelijken en de benodigde vaardigheden te ontwikkelen.

Dus, wat kun je nu doen?

Zoek online naar gratis werkbladen over schaalberekening voor groep 8. Er zijn veel websites die gratis materialen aanbieden.
Ontwerp je eigen werkblad met realistische scenario's en verschillende soorten opgaven.
Oefen regelmatig met schaalberekening, zowel in de klas als thuis.
Gebruik praktische voorbeelden om het belang van schaalberekening te benadrukken.
Maak schaalberekening leuk en boeiend door het te verbinden met de interesses van de leerlingen.

Door schaalberekening op een praktische en boeiende manier aan te pakken, kunnen we ervoor zorgen dat leerlingen de vaardigheden ontwikkelen die ze nodig hebben om te slagen in de wereld van vandaag en morgen.