Straal Cirkel Berekenen Met Omtrek

In de wiskunde is de cirkel een van de meest fundamentele en fascinerende vormen. We komen cirkels overal tegen, van de wielen van een auto tot de planeten die rond een ster draaien. Het begrijpen van de eigenschappen van een cirkel, zoals de straal en de omtrek, is cruciaal voor veel verschillende toepassingen. In dit artikel gaan we dieper in op hoe je de straal van een cirkel kunt berekenen met behulp van de omtrek.

De Basis: Omtrek en Straal

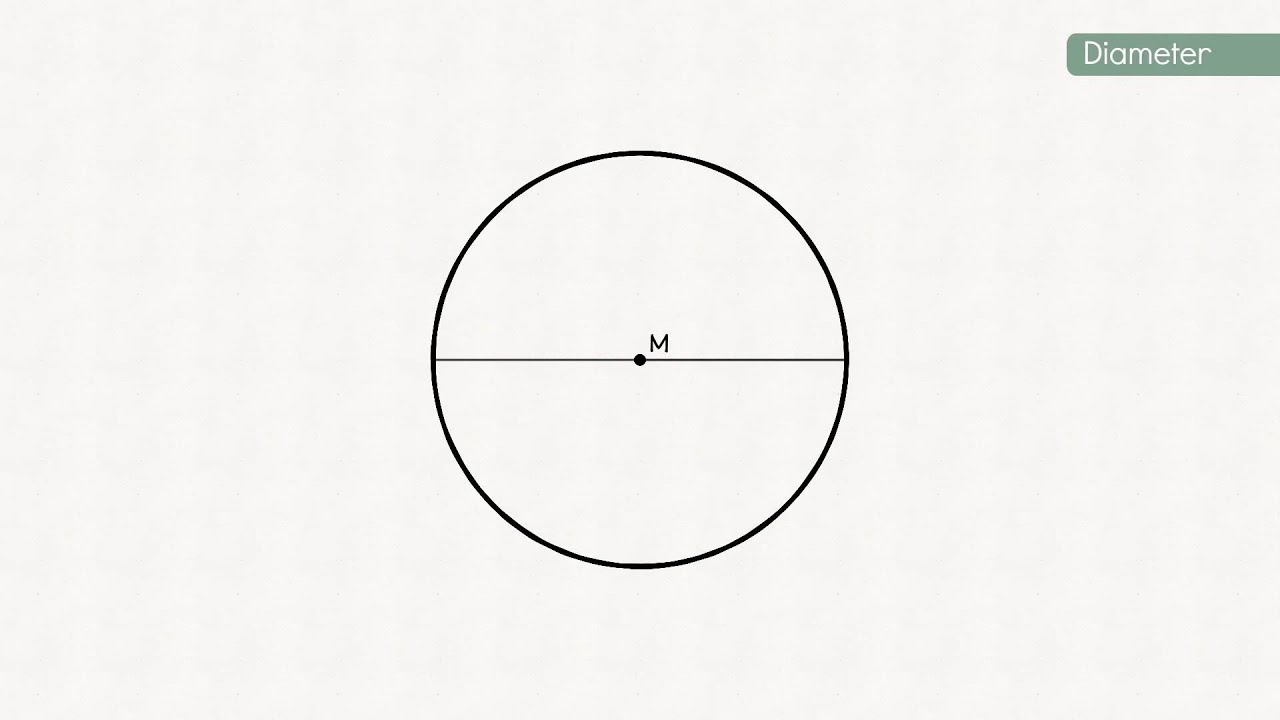
Laten we beginnen met de definities. De omtrek van een cirkel is de afstand rond de buitenrand. Stel je voor dat je een touwtje om een cirkel heenlegt; de lengte van dat touwtje is de omtrek. De straal daarentegen, is de afstand van het middelpunt van de cirkel tot een punt op de rand.

Er is een direct verband tussen de omtrek en de straal, en dit verband wordt beschreven door de volgende formule:

Omtrek (C) = 2 * π * straal (r)

Hier is π (pi) een wiskundige constante die ongeveer gelijk is aan 3.14159. Het is een irrationeel getal, wat betekent dat de decimale weergave oneindig doorgaat zonder zich te herhalen.

De Formule Herleiden

Om de straal te berekenen als je de omtrek kent, moeten we de bovenstaande formule herschrijven. We willen 'r' (de straal) isoleren aan één kant van de vergelijking. Dat doen we als volgt:

1. C = 2 * π * r

2. Deel beide zijden door 2 * π:

3. r = C / (2 * π)

Dus, de formule voor het berekenen van de straal met behulp van de omtrek is: r = C / (2π).

Stap-voor-Stap Berekening

Laten we een paar voorbeelden bekijken om de berekening te illustreren. Stel dat we een cirkel hebben met een omtrek van 25 cm. Hoe berekenen we de straal?

Stap 1: Noteer de bekende waarde. In dit geval is de omtrek (C) = 25 cm.

Stap 2: Gebruik de formule. r = C / (2π)

Stap 3: Vul de waarde in. r = 25 / (2 * 3.14159)

Stap 4: Bereken. r ≈ 25 / 6.28318 ≈ 3.98 cm

Dus, de straal van de cirkel is ongeveer 3.98 cm.

Een Ander Voorbeeld

Stel dat een boomstam een omtrek heeft van 1.8 meter. Wat is de straal van de boomstam?

Stap 1: C = 1.8 meter

Stap 2: r = C / (2π)

Stap 3: r = 1.8 / (2 * 3.14159)

Stap 4: r ≈ 1.8 / 6.28318 ≈ 0.286 meter

De straal van de boomstam is dus ongeveer 0.286 meter.

Belang van Nauwkeurigheid

De nauwkeurigheid van de berekening hangt af van de nauwkeurigheid van de waarde van π die je gebruikt. Hoewel 3.14 een veelgebruikte benadering is, kan het gebruik van een nauwkeurigere waarde, zoals de ingebouwde waarde in een rekenmachine (vaak tot 15 decimalen of meer), resulteren in een nauwkeuriger antwoord, vooral bij grotere cirkels of wanneer precisie cruciaal is.

Het is ook belangrijk om de eenheden consistent te houden. Als de omtrek in centimeters is, zal de straal ook in centimeters zijn. Als de omtrek in meters is, zal de straal in meters zijn.

Real-World Voorbeelden

Het berekenen van de straal uit de omtrek heeft tal van praktische toepassingen:

• Bouwkunde: Bij het ontwerpen van ronde structuren, zoals koepels of bruggen, is het essentieel om de straal correct te berekenen om de stabiliteit en veiligheid te garanderen.
• Engineering: Bij het vervaardigen van ronde onderdelen voor machines is precisie van cruciaal belang. Het berekenen van de straal uit de omtrek kan helpen bij het garanderen dat de onderdelen perfect passen.
• Cartografie: Bij het in kaart brengen van ronde kenmerken op aarde, zoals kratermeren, kan het berekenen van de straal helpen bij het bepalen van hun grootte en omvang.
• Landbouw: Bij het bepalen van de irrigatiebehoeften van ronde velden is de straal een belangrijke factor.
• Geneeskunde: Medische beeldvormingstechnieken, zoals MRI en CT-scans, gebruiken vaak cirkelvormige doorsneden. Het berekenen van de straal van deze structuren kan helpen bij de diagnose en behandeling van verschillende aandoeningen. Denk aan de doorsnede van een tumor of een bloedvat.

Voorbeeld Data: Stel dat een architect een koepel ontwerpt met een omtrek van 50 meter. Om de structurele integriteit te waarborgen, moet hij de straal exact weten. Met behulp van de formule r = C / (2π), berekent hij r = 50 / (2 * 3.14159) ≈ 7.96 meter. Deze precieze straal is cruciaal voor het bepalen van de benodigde materialen en het garanderen van de stabiliteit van de koepel.

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Bij het berekenen van de straal met behulp van de omtrek kunnen er fouten optreden. Hier zijn enkele veelvoorkomende fouten en hoe je ze kunt vermijden:

• Verkeerde formule: Zorg ervoor dat je de juiste formule gebruikt (r = C / (2π)). Het verwisselen van de formule leidt tot een verkeerd resultaat.
• Verkeerde waarde van π: Gebruik een nauwkeurige waarde van π. Hoewel 3.14 een redelijke benadering is, is het beter om de π-knop op je rekenmachine te gebruiken voor meer precisie.
• Eenheden negeren: Houd de eenheden consistent. Als de omtrek in centimeters is, moet de straal ook in centimeters zijn.
• Afgeronde getallen te vroeg: Rond getallen niet te vroeg af in de berekening. Wacht tot het einde om het uiteindelijke antwoord af te ronden om fouten te minimaliseren.

Tip: Controleer altijd je antwoord. Als de straal onredelijk groot of klein lijkt in verhouding tot de omtrek, controleer dan je berekeningen.

Geavanceerdere Toepassingen

Naast de basisberekeningen kan het concept van het berekenen van de straal uit de omtrek worden toegepast in complexere scenario's. Bijvoorbeeld:

• Oppervlakte van een cirkel berekenen: Zodra je de straal hebt berekend, kun je de oppervlakte van de cirkel berekenen met de formule A = π * r².
• Segmenten en sectoren: Je kunt de straal gebruiken om de oppervlakte en omtrek van segmenten en sectoren van de cirkel te bepalen.
• 3D-objecten: Het concept kan worden uitgebreid naar 3D-objecten, zoals cilinders en sferen, waar de straal een cruciale parameter is.

Deze toepassingen vereisen een dieper begrip van de geometrie, maar de basis van het berekenen van de straal uit de omtrek blijft van essentieel belang.

Conclusie

Het berekenen van de straal van een cirkel met behulp van de omtrek is een fundamentele vaardigheid in de wiskunde met veel praktische toepassingen. Door de formule r = C / (2π) te begrijpen en de stappen zorgvuldig te volgen, kun je nauwkeurige resultaten verkrijgen. Vergeet niet om aandacht te besteden aan de nauwkeurigheid van π, consistentie van de eenheden en veelvoorkomende fouten te vermijden. Dus, de volgende keer dat je een cirkelvormig object tegenkomt en alleen de omtrek kent, weet je hoe je de straal kunt berekenen!

Oefening baart kunst! Probeer zelf enkele voorbeelden te berekenen. Je kunt online calculators gebruiken om je antwoorden te controleren. Daag jezelf uit met steeds complexere problemen om je vaardigheden verder te ontwikkelen.