Straal Van Een Cirkel Berekenen

Heb je je ooit afgevraagd hoe je de straal van een cirkel kunt berekenen? Of je nu een wiskunde student bent die worstelt met geometrie, een doe-het-zelver die een rond object moet ontwerpen, of gewoon nieuwsgierig bent naar de wereld om je heen, het berekenen van de straal van een cirkel is een vaardigheid die verrassend nuttig kan zijn. In dit artikel gaan we diep in op de verschillende manieren om dit te doen, met duidelijke uitleg en praktische voorbeelden. We richten ons op een breed publiek, van beginners tot mensen met enige voorkennis van wiskunde.

Wat is de Straal van een Cirkel?

Laten we beginnen met de basis. De straal van een cirkel is de afstand van het middelpunt van de cirkel tot elk punt op de cirkelrand. Het is een fundamentele maat die gebruikt wordt om andere eigenschappen van de cirkel te berekenen, zoals de omtrek en de oppervlakte. Denk aan een fietswiel: de straal is de lengte van de spaken van het midden naar de buitenkant.

Waarom is het Belangrijk om de Straal te Kunnen Berekenen?

Het berekenen van de straal is essentieel in veel verschillende situaties:

Wiskunde en Geometrie: Het is een basisconcept in geometrische berekeningen.
Constructie en Ontwerp: Bij het ontwerpen van ronde objecten is het kennen van de straal cruciaal. Denk aan het bouwen van een koepel, het ontwerpen van een tandwiel, of het creëren van een rond zwembad.
Engineering: Ingenieurs gebruiken de straal bij het ontwerpen van roterende machines, leidingen en andere circulaire componenten.
Dagelijks Leven: Van het bepalen van de maat van een pizzapunt tot het berekenen van de hoeveelheid materiaal die nodig is voor een rond project, de straal komt vaker voor dan je denkt.

Methoden om de Straal te Berekenen

Er zijn verschillende manieren om de straal van een cirkel te berekenen, afhankelijk van welke informatie je hebt. We zullen de meest voorkomende methoden bespreken.

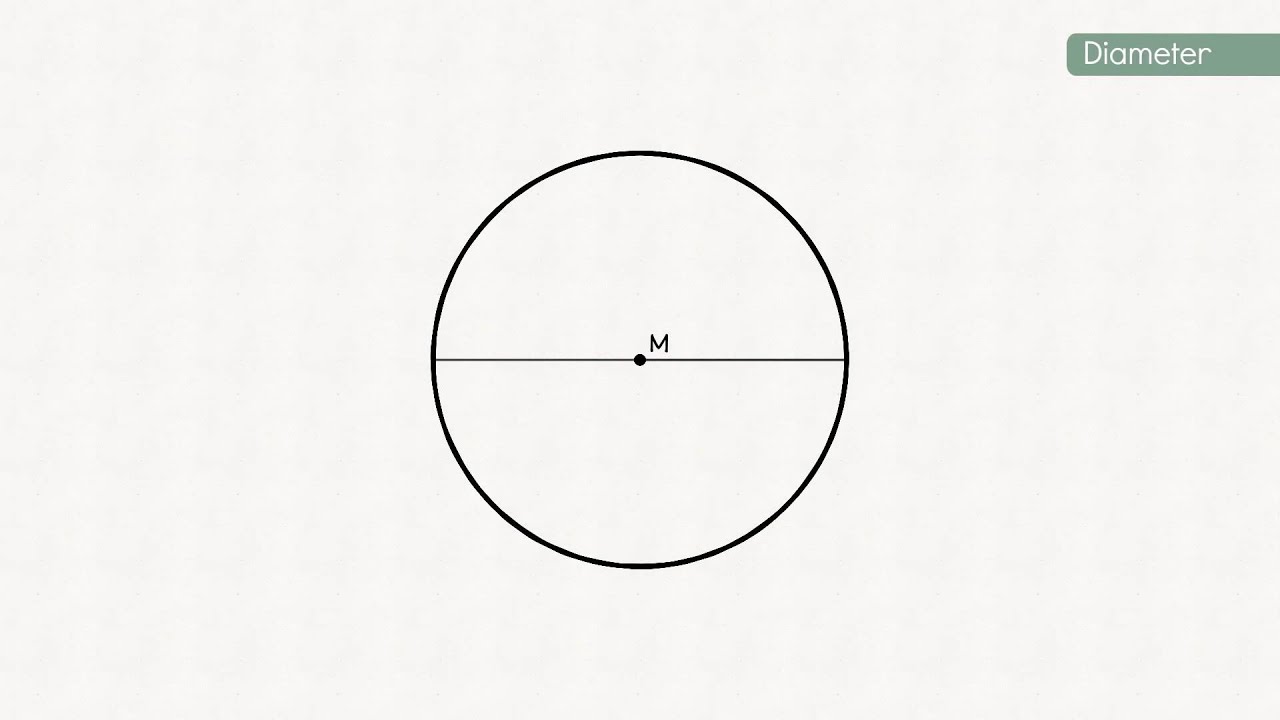
1. Via de Diameter

De diameter van een cirkel is de afstand over de cirkel, door het middelpunt. De diameter is dus twee keer de straal. Daarom is de meest eenvoudige manier om de straal te berekenen, het delen van de diameter door 2:

straal (r) = diameter (d) / 2

Voorbeeld: Als de diameter van een cirkel 10 cm is, dan is de straal 10 cm / 2 = 5 cm.

2. Via de Omtrek

De omtrek van een cirkel is de afstand rondom de cirkel. De formule voor de omtrek is:

omtrek (C) = 2 * π * straal (r)

Waarbij π (pi) een wiskundige constante is die ongeveer gelijk is aan 3.14159.

Om de straal te berekenen als je de omtrek kent, kun je de formule herschrijven:

straal (r) = omtrek (C) / (2 * π)

Voorbeeld: Als de omtrek van een cirkel 25 cm is, dan is de straal 25 cm / (2 * 3.14159) ≈ 3.98 cm.

3. Via de Oppervlakte

De oppervlakte van een cirkel is de ruimte die binnen de cirkel ligt. De formule voor de oppervlakte is:

oppervlakte (A) = π * straal (r)²

Om de straal te berekenen als je de oppervlakte kent, kun je de formule herschrijven:

straal (r) = √(oppervlakte (A) / π)

Waar √ het wortelteken is, wat betekent dat je de vierkantswortel moet nemen van het resultaat.

Voorbeeld: Als de oppervlakte van een cirkel 50 cm² is, dan is de straal √(50 cm² / 3.14159) ≈ 3.99 cm.

4. Via een Cirkelsegment

Soms heb je geen volledige cirkel, maar slechts een segment. Een cirkelsegment is een deel van een cirkel dat wordt afgesneden door een rechte lijn (een koorde). Als je de lengte van de koorde (c) en de hoogte (h) van het segment kent (de afstand van het midden van de koorde tot de cirkelrand), kun je de straal berekenen met de volgende formule:

straal (r) = (c² / (8 * h)) + (h / 2)

Voorbeeld: Stel dat je een cirkelsegment hebt met een koorde van 12 cm en een hoogte van 3 cm. De straal is dan (12² / (8 * 3)) + (3 / 2) = (144 / 24) + 1.5 = 6 + 1.5 = 7.5 cm.

5. Met behulp van coördinaten in een cartesiaans vlak

Als een cirkel in een cartesiaans vlak is weergegeven en je kent de coördinaten van het middelpunt (x₀, y₀) en een punt op de cirkel (x₁, y₁), dan kun je de straal berekenen met de afstand formule, gebaseerd op de stelling van Pythagoras:

straal (r) = √((x₁ - x₀)² + (y₁ - y₀)²)

Voorbeeld: Het middelpunt van de cirkel bevindt zich op (2, 3) en een punt op de cirkel ligt op (5, 7). De straal is dan √((5 - 2)² + (7 - 3)²) = √(3² + 4²) = √(9 + 16) = √25 = 5.

Tips en Trucs voor het Berekenen van de Straal

Gebruik de Juiste Eenheden: Zorg ervoor dat alle metingen in dezelfde eenheden zijn voordat je gaat rekenen. Bijvoorbeeld, alles in centimeters of alles in meters.
Rond Correct Af: Rond je antwoord pas af aan het einde van de berekening, om afrondingsfouten te minimaliseren.
Controleer je Antwoord: Controleer of je antwoord logisch is. Een straal kan bijvoorbeeld nooit negatief zijn.
Gebruik een Rekenmachine: Voor complexere berekeningen, gebruik een rekenmachine met een pi-knop.

Voorbeelden uit de Praktijk

Laten we eens kijken naar een paar praktische voorbeelden van hoe je de straal kunt berekenen:

Een Pizzapunt: Je wilt weten hoeveel korst je gaat eten. Je meet de lengte van de rechte kant van de pizzapunt (de koorde) en de hoogte van de punt. Met de segmentformule kun je de straal van de hele pizza schatten.
Een Rond Zwembad: Je wilt een zeil kopen om over je ronde zwembad te spannen. Je meet de omtrek van het zwembad. Met de omtrekformule kun je de straal berekenen en zo de diameter bepalen, die je nodig hebt om het juiste zeil te kopen.
Een Wiel: Je wilt het perfecte wiel ontwerpen voor een nieuwe machine. Je weet hoeveel oppervlakte het wiel moet hebben. Met de oppervlakteformule kun je de straal berekenen en zo de juiste afmetingen bepalen.

Veelgemaakte Fouten

Hier zijn een paar veelgemaakte fouten bij het berekenen van de straal:

Diameter en Straal Verwarren: Onthoud dat de diameter twee keer de straal is.
Pi Vergeten: Vergeet niet de waarde van pi (π) te gebruiken in de formules voor omtrek en oppervlakte.
Verkeerde Formule Gebruiken: Gebruik de juiste formule op basis van de informatie die je hebt.
Eenheden Negeren: Zorg ervoor dat alle metingen in dezelfde eenheden zijn.

Conclusie

Het berekenen van de straal van een cirkel is een fundamentele vaardigheid met veel toepassingen in de wiskunde, wetenschap, engineering, en het dagelijks leven. Door de verschillende methoden die we hebben besproken te begrijpen, kun je de straal berekenen op basis van de beschikbare informatie, of het nu de diameter, de omtrek, de oppervlakte, of een cirkelsegment is. Met de tips en trucs die we hebben gedeeld, kun je veelgemaakte fouten vermijden en nauwkeurige resultaten behalen. Dus, de volgende keer dat je een cirkel tegenkomt, wees niet bang om de straal te berekenen! Je hebt nu de kennis en de tools om het met vertrouwen te doen. Gebruik deze kennis om actief de wereld om je heen te meten en te begrijpen. Succes!