Wat Is De Oppervlakte Van Een Cirkel

Heb je je ooit afgevraagd hoe je de oppervlakte van een pizzapunt berekent, of hoeveel materiaal je nodig hebt om de bodem van een ronde taartvorm te bedekken? Misschien sta je voor een praktisch probleem in de tuin, waarbij je de benodigde hoeveelheid graszaad voor een cirkelvormig bloembed moet inschatten. Al deze situaties draaien om één fundamentele vraag: Wat is de oppervlakte van een cirkel? En belangrijker nog, hoe bereken je die?

Geen zorgen, wiskunde kan soms intimiderend lijken, maar de formule voor de oppervlakte van een cirkel is verrassend eenvoudig en toepasbaar in talloze situaties. We gaan deze formule ontleden, stap voor stap, zodat je hem kunt begrijpen en zelf kunt toepassen.

De Basis: Diameter, Radius en Pi (π)

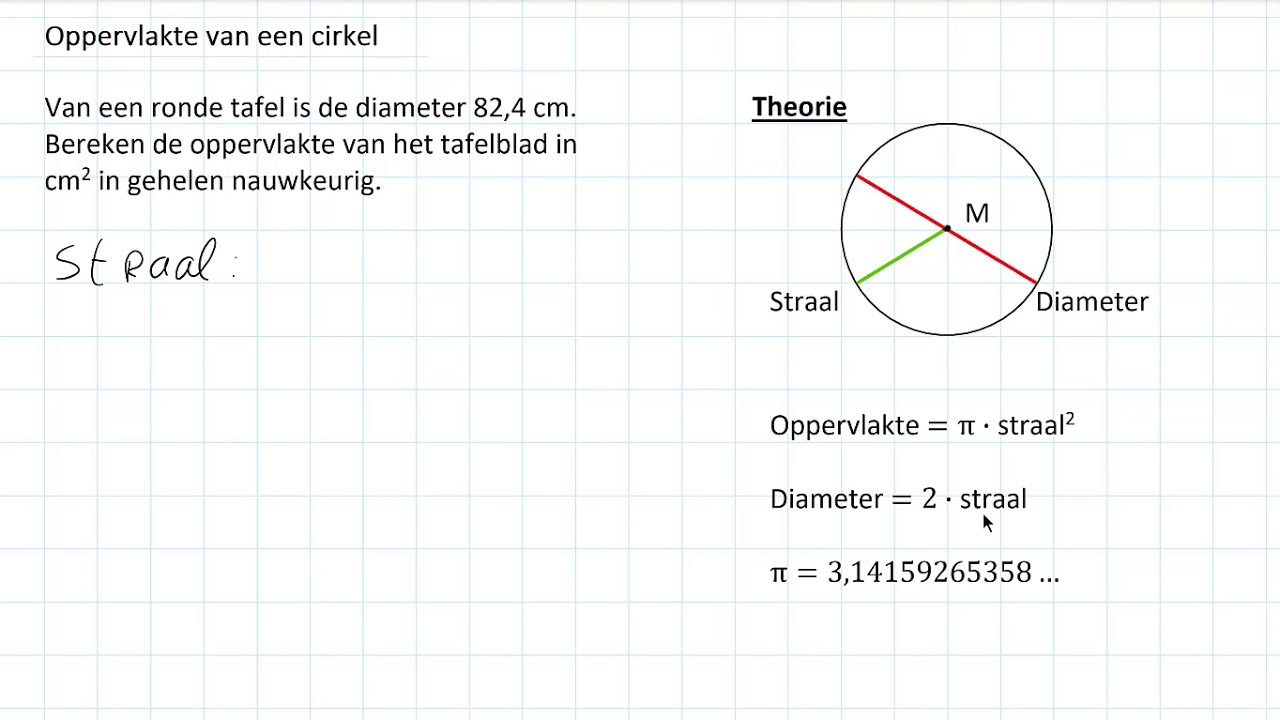
Voordat we duiken in de formule, is het cruciaal om enkele basisbegrippen te begrijpen. Een cirkel is een perfect ronde vorm waarbij alle punten op de rand dezelfde afstand hebben tot het middelpunt. Die afstand noemen we de radius (r). De afstand van de ene kant van de cirkel naar de andere, die door het middelpunt loopt, noemen we de diameter (d). De diameter is dus twee keer de radius (d = 2r).

En dan is er nog Pi (π). Dit is een speciale wiskundige constante die de verhouding weergeeft tussen de omtrek van een cirkel en zijn diameter. Pi is een irrationeel getal, wat betekent dat het oneindig veel decimalen heeft zonder een herhalend patroon. We gebruiken vaak de benadering 3,14, maar voor nauwkeurigere berekeningen kun je een rekenmachine gebruiken die een nauwkeurigere waarde van Pi heeft.

Waarom is Pi zo Belangrijk?

Pi is niet zomaar een getal; het is essentieel voor het berekenen van de omtrek en oppervlakte van cirkels. Zonder Pi zouden we deze berekeningen niet kunnen uitvoeren. De letter π is gekozen als symbool omdat het de eerste letter is van het Griekse woord περιφέρεια (peripheria), wat "omtrek" betekent.

De Formule: A = πr²

Nu komen we tot de kern van de zaak: de formule voor de oppervlakte van een cirkel. De formule is als volgt:

A = πr²

Waarbij:

• A staat voor de oppervlakte van de cirkel.
• π (Pi) is ongeveer 3,14.
• r staat voor de radius van de cirkel.
• r² betekent "radius in het kwadraat" (radius vermenigvuldigd met zichzelf).

Met andere woorden, om de oppervlakte van een cirkel te vinden, kwadrateer je de radius en vermenigvuldig je het resultaat met Pi.

Hoe Gebruik je de Formule: Een Stappenplan

Laten we dit nu in een stappenplan gieten, zodat je het gemakkelijk kunt volgen:

1. Bepaal de radius (r) van de cirkel. Als je de diameter hebt, deel deze dan door 2 om de radius te vinden.
2. Kwadrateer de radius. Vermenigvuldig de radius met zichzelf (r * r).
3. Vermenigvuldig het resultaat met Pi (π). Gebruik de benadering 3,14 of de Pi-knop op je rekenmachine voor een nauwkeuriger resultaat.
4. De uitkomst is de oppervlakte van de cirkel! Vergeet niet om de juiste eenheid toe te voegen (bijvoorbeeld vierkante centimeters, vierkante meters, etc.).

Voorbeelden uit de Praktijk

Laten we een paar voorbeelden bekijken om het duidelijker te maken:

Voorbeeld 1: Een pizzapunt

Stel, je hebt een pizzapunt met een radius van 10 cm. Wat is de oppervlakte van de pizzapunt?

1. Radius (r) = 10 cm
2. r² = 10 cm * 10 cm = 100 cm²
3. A = π * 100 cm² ≈ 3,14 * 100 cm² = 314 cm²

De oppervlakte van de pizzapunt is ongeveer 314 vierkante centimeter.

Voorbeeld 2: Een rond bloembed

Je wilt een rond bloembed aanleggen met een diameter van 2 meter. Hoeveel graszaad heb je nodig om het bloembed te bedekken?

1. Diameter (d) = 2 meter, dus radius (r) = d / 2 = 1 meter
2. r² = 1 meter * 1 meter = 1 m²
3. A = π * 1 m² ≈ 3,14 * 1 m² = 3,14 m²

Je hebt ongeveer 3,14 vierkante meter graszaad nodig.

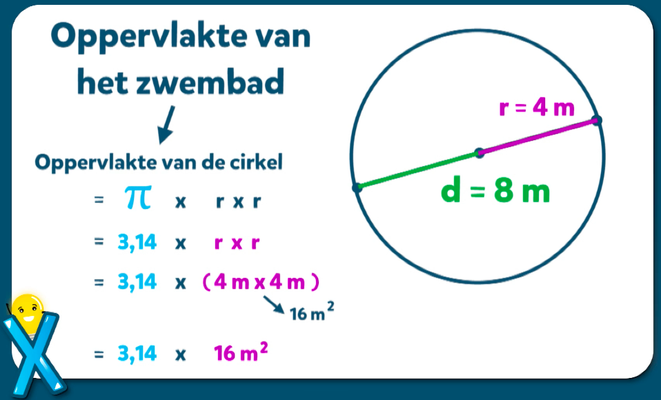
Voorbeeld 3: Een zwembad

Een rond zwembad heeft een radius van 5 meter. Wat is de oppervlakte van het zwembad?

1. Radius (r) = 5 meter
2. r² = 5 meter * 5 meter = 25 m²
3. A = π * 25 m² ≈ 3,14 * 25 m² = 78,5 m²

De oppervlakte van het zwembad is ongeveer 78,5 vierkante meter.

Tips voor Nauwkeurigheid

Hoewel 3,14 een handige benadering is voor Pi, levert het gebruik van een rekenmachine met een Pi-knop een nauwkeuriger resultaat op. Dit is vooral belangrijk bij grotere cirkels of wanneer precisie cruciaal is. Als je met complexe problemen werkt, is het ook handig om tussenberekeningen niet af te ronden, maar pas aan het einde het definitieve antwoord af te ronden. Dit minimaliseert afrondingsfouten.

Daarnaast is het belangrijk om altijd de juiste eenheden te gebruiken. Als de radius in centimeters is, is de oppervlakte in vierkante centimeters. Als de radius in meters is, is de oppervlakte in vierkante meters, enzovoort.

Veelgemaakte Fouten

Een veelgemaakte fout is het vergeten om de radius te kwadrateren. Vergeet niet dat de formule πr² is, dus je moet de radius eerst vermenigvuldigen met zichzelf voordat je met Pi vermenigvuldigt. Een andere fout is het verwarren van de diameter met de radius. Zorg ervoor dat je de juiste waarde gebruikt in de formule. Als je de diameter hebt gekregen, deel deze dan eerst door 2 om de radius te vinden.

Toepassingen Buiten de Wiskundeles

De formule voor de oppervlakte van een cirkel is niet alleen nuttig in wiskundelessen. Het heeft talloze toepassingen in het dagelijks leven en in verschillende vakgebieden. Architecten gebruiken het om ronde gebouwen en structuren te ontwerpen. Ingenieurs gebruiken het om de capaciteit van ronde tanks en leidingen te berekenen. Landmeters gebruiken het om de oppervlakte van ronde percelen te bepalen. Zelfs bij het bakken, zoals we aan het begin al zagen, kan het handig zijn voor het bepalen van de juiste grootte van een taartvorm.

Ook in de wetenschap is de formule onmisbaar. Denk aan het berekenen van de oppervlakte van een lens in een telescoop, of het bepalen van de doorsnede van een boomstam bij ecologisch onderzoek.

Conclusie

De oppervlakte van een cirkel berekenen is eenvoudiger dan je misschien dacht. Met de formule A = πr² en een beetje oefening kun je deze berekening in allerlei situaties toepassen. Of je nu een pizza bestelt, een tuin ontwerpt of een wetenschappelijk probleem oplost, de kennis van deze formule is een waardevolle tool.

Dus, de volgende keer dat je een cirkel ziet, denk dan even na over de wiskunde erachter. Je zult versteld staan ​​hoe vaak dit fundamentele concept in de wereld om ons heen voorkomt. Wiskunde is overal!