Wat Is De Straal Van Een Cirkel

Ken je dat gevoel? Je staat voor een cirkel, bijvoorbeeld een pizzapunt of een zwembad, en je weet dat er belangrijke informatie verborgen zit in die perfect ronde vorm. Eén van die stukjes informatie is de straal. Misschien heb je er vaag iets over gehoord in de wiskundeles, maar wat is het precies en waarom is het zo belangrijk? Geen zorgen, we gaan het samen ontdekken!

Wat is de straal van een cirkel?

De straal van een cirkel is, heel simpel gezegd, de afstand van het middelpunt van de cirkel tot een willekeurig punt op de cirkelrand. Stel je voor dat je een touwtje hebt. Je houdt het ene uiteinde vast in het midden van de pizza, en het andere uiteinde raakt de korst. De lengte van dat touwtje is de straal.

Belangrijk: De straal is altijd dezelfde, ongeacht welk punt op de cirkelrand je kiest. Daarom is een cirkel zo'n perfecte vorm.

Om het nog duidelijker te maken, laten we een paar begrippen kort herhalen:

Middelpunt: Het exacte midden van de cirkel.
Cirkelrand (omtrek): De 'lijn' die de cirkel vormt.
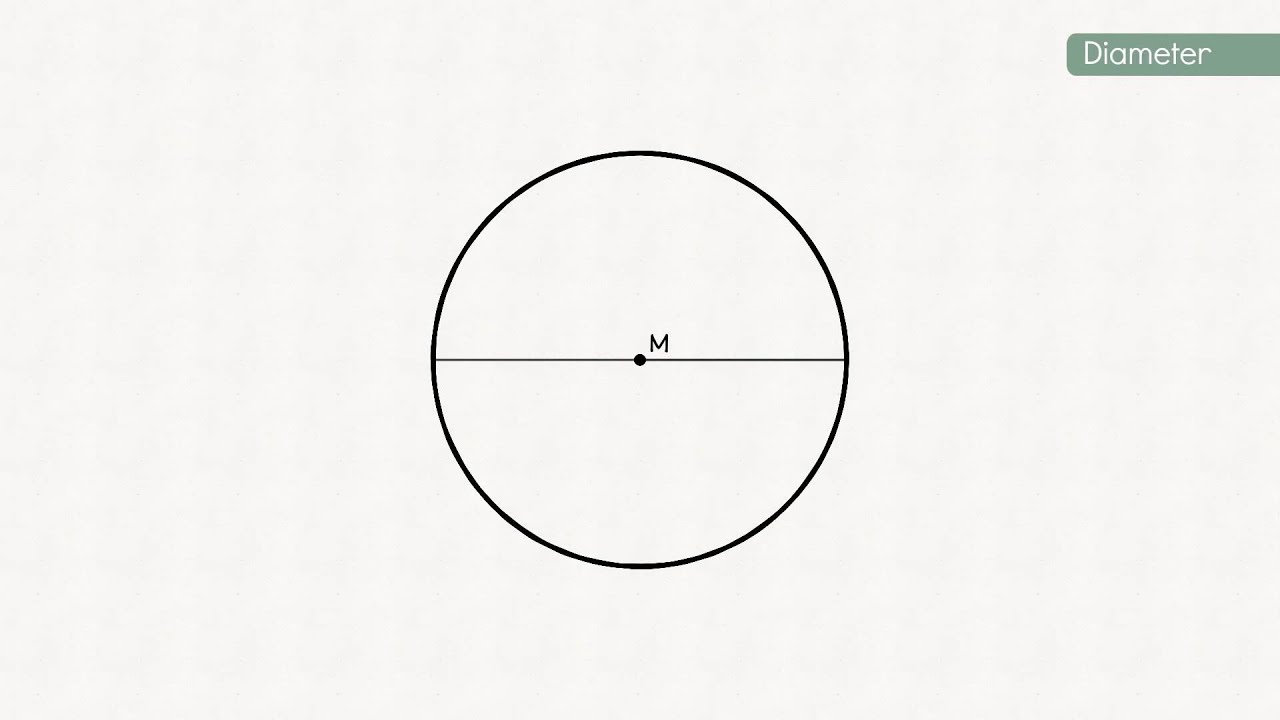
Diameter: Een lijnstuk dat van de ene kant van de cirkel naar de andere loopt, door het middelpunt. De diameter is dus twee keer zo lang als de straal!

Waarom is de straal zo belangrijk?

De straal is niet zomaar een lijntje. Het is een essentiële bouwsteen voor het berekenen van andere belangrijke eigenschappen van de cirkel, zoals:

Oppervlakte: De ruimte binnen de cirkel.
Omtrek: De lengte van de cirkelrand (hoe ver is het rondje?).
Volume (van een cilinder of bol): Als de cirkel de basis is van een 3D-vorm, heb je de straal nodig om het volume te berekenen.

Zonder de straal zouden we deze berekeningen niet kunnen maken. Dat zou nogal lastig zijn bij het ontwerpen van bijvoorbeeld wielen, pijpleidingen of satellieten!

Hoe bereken je de straal?

Er zijn verschillende manieren om de straal te berekenen, afhankelijk van wat je al weet over de cirkel. Hier zijn de meest voorkomende methoden:

1. Als je de diameter weet:

Dit is de simpelste methode. Zoals we al eerder zeiden, is de diameter twee keer zo lang als de straal. Dus:

Straal = Diameter / 2

Bijvoorbeeld: Als de diameter van een bord 30 cm is, dan is de straal 30 cm / 2 = 15 cm.

2. Als je de omtrek weet:

De omtrek van een cirkel is 2 * π * straal (waarbij π (pi) ongeveer 3.14159 is). Dus:

Straal = Omtrek / (2 * π)

Bijvoorbeeld: Stel dat de omtrek van een boomstam 157 cm is. Dan is de straal ongeveer 157 cm / (2 * 3.14159) = 25 cm.

3. Als je de oppervlakte weet:

De oppervlakte van een cirkel is π * straal². Dus:

Straal = √(Oppervlakte / π)

Let op: de √ betekent de vierkantswortel.

Bijvoorbeeld: Als de oppervlakte van een vijver 78.5 m² is, dan is de straal ongeveer √(78.5 m² / 3.14159) = 5 m.

Praktische voorbeelden: Wanneer heb je de straal nodig?

De straal is niet alleen belangrijk in wiskundeboeken. Je komt het in het dagelijks leven veel vaker tegen dan je denkt:

Koken en bakken: De grootte van een taartvorm wordt vaak aangegeven in diameter, maar je hebt de straal nodig om de hoeveelheid deeg te berekenen.
Tuinieren: Bij het aanleggen van een ronde bloembed of vijver is de straal belangrijk voor het bepalen van de benodigde materialen.
Constructie: Architecten en ingenieurs gebruiken de straal bij het ontwerpen van gebouwen, bruggen en andere constructies met ronde vormen.
Sport: Bij het berekenen van de afstanden in atletiek, zoals de loopafstand op een atletiekbaan, is de straal van de bochten essentieel.
Techniek: Bij het ontwerpen van tandwielen, katrollen en andere mechanische onderdelen is de straal een cruciale factor.

Tips om de straal makkelijker te begrijpen:

Visualiseer: Teken een cirkel en markeer het middelpunt en de straal.
Gebruik voorwerpen: Meet de straal van alledaagse objecten, zoals een beker of een munt.
Oefen: Maak oefenopgaven om de formules te leren en toe te passen. Er zijn online genoeg resources te vinden!
Gebruik een rekenmachine: Veel rekenmachines hebben een π-knop en een vierkantswortel-functie, wat het berekenen van de straal makkelijker maakt.

Veelgemaakte fouten en hoe je ze vermijdt:

Diameter en straal verwarren: Onthoud dat de diameter twee keer zo lang is als de straal.
Verkeerde formule gebruiken: Zorg ervoor dat je de juiste formule gebruikt, afhankelijk van wat je al weet (diameter, omtrek of oppervlakte).
Rekenfouten: Controleer je berekeningen zorgvuldig, vooral bij het gebruik van π en de vierkantswortel.
Eenheden vergeten: Zorg ervoor dat je de juiste eenheden gebruikt (bijvoorbeeld cm, m, inch) en dat je de eenheden consistent houdt.

Bijvoorbeeld: Als je werkt met meters (m) voor de oppervlakte, moet je de straal ook in meters (m) berekenen.

Conclusie:

De straal van een cirkel is een fundamenteel concept in de wiskunde, met talloze toepassingen in het dagelijks leven. Door te begrijpen wat de straal is en hoe je deze kunt berekenen, krijg je een beter inzicht in de wereld om je heen en ben je beter voorbereid op praktische problemen. Hopelijk heeft dit artikel je geholpen om de straal van een cirkel beter te begrijpen! Blijf oefenen en experimenteren, en je zult zien dat wiskunde helemaal niet zo ingewikkeld hoeft te zijn.

Nog even herhalen:

De straal is de afstand van het middelpunt tot de cirkelrand. De diameter is 2 keer de straal. Met de straal kun je de omtrek en de oppervlakte van een cirkel berekenen.