Wat Is Een Evenwijdige Lijn

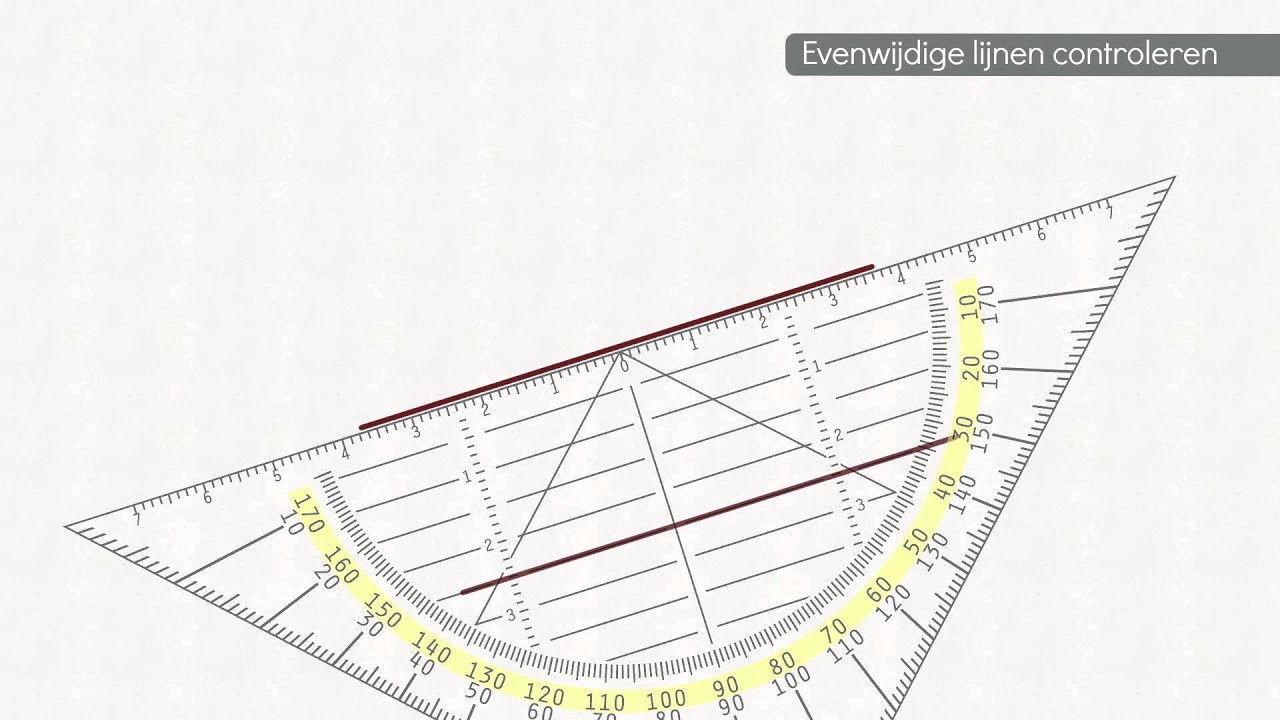
Stel je voor: je staat langs een spoorweg. Kijk naar de twee rails. Zie je hoe ze, hoe ver je ook kijkt, altijd dezelfde afstand tot elkaar houden? Dat is in de essentie wat evenwijdige lijnen zijn. Dit artikel is bedoeld voor iedereen die meer wil begrijpen over basisprincipes van meetkunde, van leerlingen die wiskunde studeren tot nieuwsgierige geesten die hun kennis willen opfrissen.

Wat zijn Evenwijdige Lijnen?

Simpel gezegd, evenwijdige lijnen zijn lijnen in een vlak die elkaar nooit kruisen of snijden, ongeacht hoe ver ze worden doorgetrokken. Het belangrijkste kenmerk is dat ze altijd dezelfde afstand tot elkaar bewaren. Deze afstand wordt gemeten langs een lijn die loodrecht staat op beide evenwijdige lijnen.

Definitie in Formele Termen

Wiskundig gezien worden twee lijnen als evenwijdig beschouwd als ze dezelfde helling (of richtingscoëfficiënt) hebben en zich in hetzelfde vlak bevinden. De notatie voor evenwijdigheid is: l1 || l2, wat betekent "lijn l1 is evenwijdig aan lijn l2".

Belangrijk: Twee lijnen in de ruimte die elkaar niet snijden, zijn niet automatisch evenwijdig. Ze kunnen kruisende (skew) lijnen zijn. Denk aan twee vliegroutes die elkaar nooit kruisen, maar ook niet in hetzelfde vlak liggen; deze zijn niet evenwijdig, maar kruisend.

Kenmerken van Evenwijdige Lijnen

Naast het feit dat ze elkaar nooit snijden, hebben evenwijdige lijnen een aantal belangrijke eigenschappen:

Constante Afstand: De afstand tussen twee evenwijdige lijnen blijft altijd hetzelfde.
Gelijke Helling: In een Cartesiaans coördinatenstelsel hebben evenwijdige lijnen dezelfde helling. De helling (m) wordt berekend als de verandering in y gedeeld door de verandering in x (m = Δy/Δx).
Transversaal en Hoeken: Wanneer een lijn (de transversaal) twee evenwijdige lijnen snijdt, ontstaan er verschillende paren hoeken die speciale relaties hebben:

Overstaande hoeken zijn gelijk.
Verwisselende binnenhoeken zijn gelijk.
Verwisselende buitenhoeken zijn gelijk.
Corresponderende hoeken zijn gelijk.
Binnenhoeken aan dezelfde kant van de transversaal zijn supplementair (som is 180 graden).

Waar komen Evenwijdige Lijnen voor?

Evenwijdige lijnen zijn overal om ons heen, zowel in de natuur als in door de mens gemaakte objecten:

Architectuur: Muren, vloeren, en daklijnen van gebouwen zijn vaak opgebouwd uit evenwijdige lijnen. Denk aan de lijnen van een bakstenen muur of de planken van een houten vloer.
Transport: Spoorwegen, wegen (vooral rijstroken) en start- en landingsbanen van vliegvelden maken gebruik van het principe van evenwijdige lijnen.
Design: Patronen op behang, stoffen, en grafische ontwerpen bevatten vaak evenwijdige lijnen.
Natuur: Hoewel minder direct, kun je in de structuur van kristallen of de nerven van bladeren soms benaderingen van evenwijdige lijnen vinden.

Door deze voorbeelden te herkennen, begin je te zien hoe fundamenteel het concept van evenwijdige lijnen is in de wereld om ons heen.

Hoe herken je Evenwijdige Lijnen?

Er zijn verschillende manieren om te bepalen of lijnen evenwijdig zijn, afhankelijk van de informatie die je hebt:

Visuele Inspectie: Als je twee lijnen visueel kunt inspecteren en ze lijken nooit te snijden, en de afstand tussen hen lijkt constant te blijven, dan zijn ze waarschijnlijk evenwijdig. Echter, visuele inspectie is niet altijd accuraat, vooral niet bij kleine afwijkingen.
Meten van Afstand: Meet de afstand tussen de twee lijnen op verschillende punten. Als de afstand constant blijft, zijn de lijnen evenwijdig.
Bepalen van de Helling: Als je de vergelijkingen van de lijnen hebt (bijvoorbeeld in de vorm y = mx + b), bepaal dan de helling (m) van elke lijn. Als de hellingen gelijk zijn, zijn de lijnen evenwijdig.
Hoekrelaties bij een Transversaal: Als een lijn twee andere lijnen snijdt (een transversaal), meet dan de hoeken die gevormd worden. Als de verwisselende binnenhoeken, verwisselende buitenhoeken, of corresponderende hoeken gelijk zijn, of als de binnenhoeken aan dezelfde kant van de transversaal supplementair zijn, dan zijn de lijnen evenwijdig.

Voorbeeld: Stel dat je twee lijnen hebt, gegeven door de vergelijkingen y = 2x + 3 en y = 2x - 1. Beide lijnen hebben een helling van 2. Omdat hun hellingen gelijk zijn, zijn deze lijnen evenwijdig.

Evenwijdige Lijnen en Meetkundige Constructies

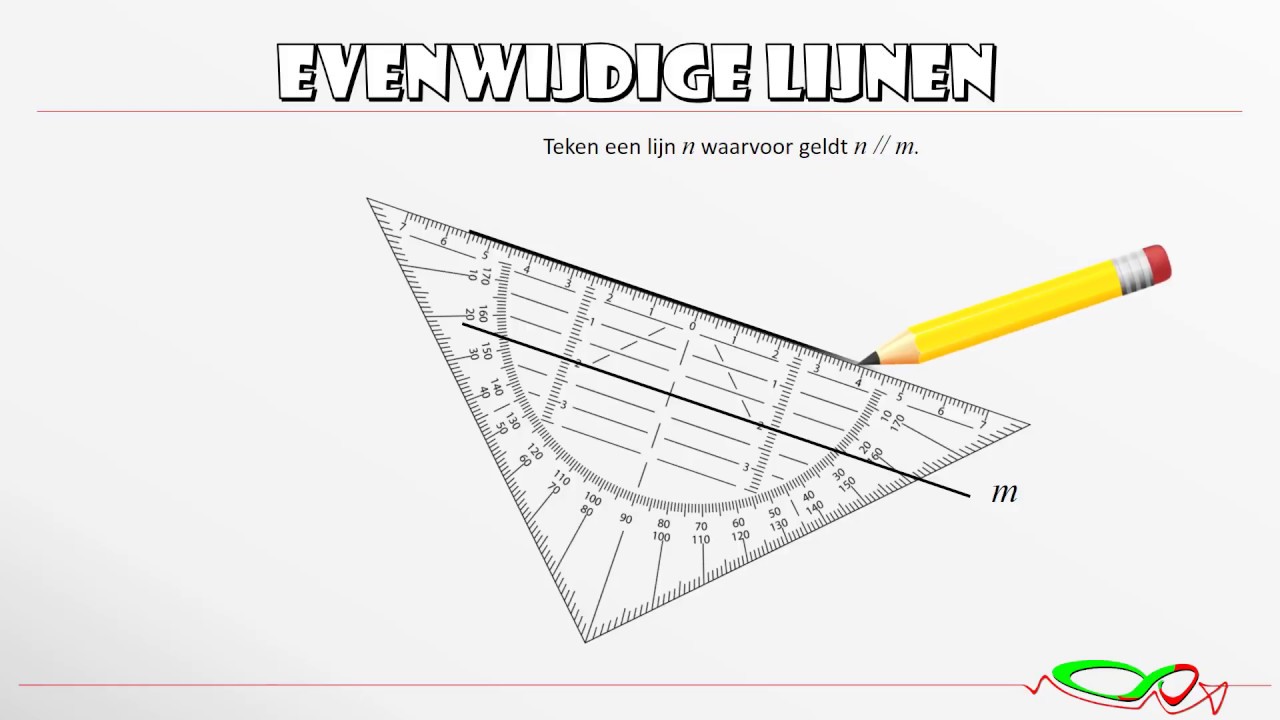
Het construeren van evenwijdige lijnen is een fundamentele vaardigheid in de meetkunde. Je kunt een passer en liniaal gebruiken om nauwkeurig evenwijdige lijnen te tekenen. Hier is een algemene methode:

Gegeven: Een lijn l en een punt P dat niet op de lijn l ligt.
Stap 1: Teken een lijn door punt P die de lijn l snijdt (dit is je transversaal). Noem het snijpunt A.
Stap 2: Gebruik een passer om een boog te tekenen met het middelpunt in A, die zowel de transversaal als de lijn l snijdt.
Stap 3: Verplaats de passer naar punt P en teken een boog met dezelfde straal die de transversaal snijdt.
Stap 4: Meet de afstand tussen de twee snijpunten op lijn l (van de eerste boog).
Stap 5: Plaats de passer op het snijpunt van de tweede boog met de transversaal en teken een boog met de zojuist gemeten afstand. Dit creëert een nieuw snijpunt.
Stap 6: Teken een lijn door punt P en het nieuwe snijpunt. Deze lijn is evenwijdig aan lijn l.

Deze constructie is gebaseerd op het principe dat corresponderende hoeken gelijk zijn wanneer een transversaal twee evenwijdige lijnen snijdt.

Waarom zijn Evenwijdige Lijnen Belangrijk?

Het concept van evenwijdige lijnen is niet alleen theoretisch; het heeft praktische toepassingen in verschillende vakgebieden:

Architectuur en Engineering: Zorgen voor stabiliteit en symmetrie in structuren. Denk aan het recht en stabiel houden van muren en vloeren.
Cartografie en Navigatie: Voor het creëren van kaarten en het bepalen van routes. Lijnen op kaarten die de lengte- en breedtegraden vertegenwoordigen, zijn een goed voorbeeld.
Computer Graphics en Design: Voor het creëren van perspectief en het manipuleren van objecten in de ruimte.
Wiskunde en Natuurwetenschappen: Als fundamenteel concept in de meetkunde, calculus en andere disciplines.

Door evenwijdige lijnen te begrijpen, ontwikkel je een beter ruimtelijk inzicht en een sterkere basis voor het oplossen van problemen in diverse contexten.

Veelvoorkomende Misvattingen

Er zijn een paar veelvoorkomende misvattingen over evenwijdige lijnen die het belangrijk is om te verhelderen:

Niet-snijdende lijnen zijn altijd evenwijdig: Zoals eerder vermeld, geldt dit alleen in een vlak. In de ruimte kunnen lijnen die elkaar niet snijden kruisend zijn.
Evenwijdige lijnen zijn altijd horizontaal of verticaal: Evenwijdige lijnen kunnen elke oriëntatie hebben, zolang ze dezelfde helling hebben.
Het is moeilijk om evenwijdige lijnen met het blote oog te herkennen: Hoewel visuele inspectie kan helpen, is het belangrijk om meetkundige principes toe te passen voor nauwkeurigheid.

Conclusie

Evenwijdige lijnen zijn een fundamenteel concept in de meetkunde en hebben praktische toepassingen in de wereld om ons heen. Van architectuur tot navigatie, het begrijpen van de eigenschappen en relaties van evenwijdige lijnen stelt je in staat om de wereld op een nieuwe manier te zien en problemen effectiever op te lossen. Door de definities, kenmerken en voorbeelden in dit artikel te bestuderen, heb je hopelijk een stevige basis gelegd om je kennis van de meetkunde verder uit te breiden. Blijf oefenen met constructies en het herkennen van evenwijdige lijnen in je omgeving, en je zult versteld staan van de veelzijdigheid en het belang van dit eenvoudige, maar krachtige concept.