Wat Is Een Kwadratisch Verband

Heb je je ooit afgevraagd hoe die bal zo'n perfecte boog maakt tijdens een basketbalwedstrijd? Of hoe ingenieurs bruggen ontwerpen die de krachten van de natuur kunnen weerstaan? Vaak ligt de sleutel in een fundamenteel wiskundig concept: het kwadratisch verband. Misschien klinkt het ingewikkeld, maar ik ga je laten zien dat het eigenlijk best wel logisch is en dat je het overal om je heen ziet.

Veel mensen associëren wiskunde met abstracte formules en saaie berekeningen. Ze vragen zich af: "Waar heb ik dit in de praktijk voor nodig?". Het is een begrijpelijke frustratie. Maar juist kwadratische verbanden laten zien hoe wiskunde een praktische tool is die ons helpt de wereld beter te begrijpen en te voorspellen. In dit artikel duiken we in de wereld van kwadratische verbanden, leggen we uit wat ze zijn, hoe ze werken en waar je ze tegenkomt.

Wat is een kwadratisch verband?

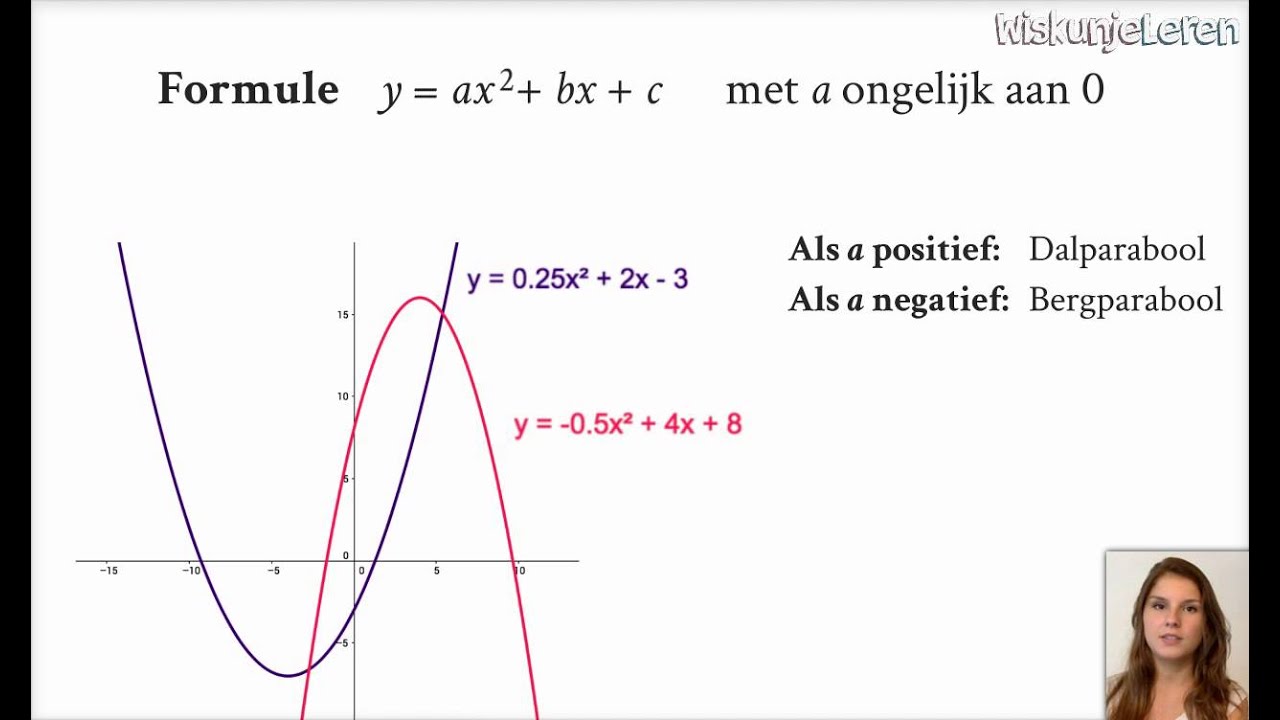
In de kern is een kwadratisch verband een wiskundige relatie tussen twee variabelen waarbij de ene variabele (meestal aangeduid als 'y') afhankelijk is van het kwadraat van de andere variabele (meestal 'x'). Dit betekent dat wanneer 'x' verandert, 'y' verandert met een snelheid die niet constant is. De algemene formule voor een kwadratisch verband is:

y = ax² + bx + c

Waar:

'y' de afhankelijke variabele is
'x' de onafhankelijke variabele is
'a', 'b' en 'c' constanten zijn die de vorm en positie van de grafiek bepalen

Het belangrijkste element is de x² term. Die zorgt voor de karakteristieke paraboolvorm wanneer je het verband grafisch weergeeft. Stel je voor dat je een bal omhoog gooit. De baan die de bal volgt is een parabool - precies de vorm die een kwadratisch verband beschrijft.

De Parabool: De Grafische Weergave

De grafiek van een kwadratisch verband is dus een parabool. Deze parabool heeft een paar belangrijke kenmerken:

Top (vertex): Dit is het hoogste of laagste punt van de parabool. Het vertegenwoordigt het maximum of minimum van de functie.
Symmetrie-as: Een verticale lijn die door de top loopt en de parabool in twee gelijke helften verdeelt.
Nulpunten (wortels): De punten waar de parabool de x-as snijdt. Dit zijn de waarden van 'x' waarvoor y = 0.

De waarde van 'a' in de formule y = ax² + bx + c bepaalt of de parabool naar boven (a > 0) of naar beneden (a < 0) geopend is. Het bepaalt ook hoe "breed" of "smal" de parabool is. Een grote absolute waarde van 'a' resulteert in een smalle parabool, terwijl een kleine absolute waarde resulteert in een brede parabool.

Kwadratische Verbanden in de Praktijk

Zoals gezegd, kwadratische verbanden zijn overal om ons heen. Hier zijn een paar voorbeelden:

Projectielbeweging: De baan van een projectiel (zoals een bal die gegooid wordt) wordt beschreven door een kwadratisch verband. De verticale positie van de bal verandert in de tijd volgens een parabool.
Bruggenbouw: Ingenieurs gebruiken kwadratische vergelijkingen om de vorm van bruggen te ontwerpen. Parabolische bruggen zijn sterk en efficiënt omdat ze de krachten gelijkmatig verdelen.
Satelliet schotels: De vorm van een satelliet schotel is ook parabolisch. Deze vorm zorgt ervoor dat signalen die de schotel bereiken, worden gefocust op één punt, waar de ontvanger zich bevindt.
Winstmaximalisatie: Bedrijven kunnen kwadratische functies gebruiken om hun winst te maximaliseren. Door kosten en opbrengsten te modelleren, kunnen ze de optimale prijs en productieniveaus bepalen.
De val van een object: De afstand die een object valt onder invloed van de zwaartekracht neemt kwadratisch toe met de tijd. Dit is te zien aan de formule s = ½gt², waarbij 's' de afstand is, 'g' de gravitatieconstante en 't' de tijd.

Stel je voor dat je een app ontwikkelt die de baan van een golfbal simuleert. Je zou een kwadratisch verband gebruiken om de hoogte van de bal op elk punt in de tijd te berekenen, rekening houdend met factoren zoals de beginsnelheid en de hoek van de slag. Of denk aan een architect die een zonnescherm ontwerpt. Met behulp van een kwadratische functie kan de architect de optimale vorm van het scherm bepalen om de hoeveelheid zonlicht die een gebouw binnenkomt te minimaliseren tijdens de heetste uren van de dag.

Counterpoints en Misvattingen

Soms wordt beweerd dat kwadratische verbanden te complex zijn om in de praktijk te gebruiken, of dat er andere, eenvoudigere modellen beschikbaar zijn. Het is waar dat soms andere modellen een goede benadering kunnen geven. Echter, de nauwkeurigheid en de mogelijkheid om complexe fenomenen te beschrijven maken kwadratische modellen vaak onvervangbaar, vooral wanneer precisie belangrijk is.

Een andere misvatting is dat kwadratische verbanden alleen relevant zijn in de exacte wetenschappen en engineering. Zoals we hebben gezien in het voorbeeld van winstmaximalisatie, kunnen ze ook zeer nuttig zijn in de economie en het bedrijfsleven. Het gaat erom dat je de relatie tussen variabelen herkent en de wiskundige tools gebruikt die het beste bij die relatie passen.

Hoe los je problemen met kwadratische verbanden op?

Er zijn verschillende methoden om problemen met kwadratische verbanden op te lossen:

Ontbinden in factoren: Deze methode werkt wanneer de kwadratische vergelijking kan worden geschreven als het product van twee lineaire factoren.
De kwadratische formule: Dit is een algemene formule die altijd werkt, ongeacht of de vergelijking kan worden ontbonden of niet. De formule is:

x = (-b ± √(b² - 4ac)) / 2a

Kwadraat afsplitsen: Deze methode is handig om de vergelijking in een vorm te brengen waaruit de top van de parabool direct kan worden afgelezen.
Grafisch: Je kunt de grafiek van de kwadratische functie tekenen en de nulpunten aflezen. Dit is vooral handig als je een visuele representatie van het probleem wilt.

Welke methode je kiest, hangt af van de specifieke vergelijking en van je persoonlijke voorkeur. Het is belangrijk om verschillende technieken te leren, zodat je flexibel bent en de meest efficiënte aanpak kunt kiezen.

Voorbeeld: Een Basketbal Worp

Laten we teruggaan naar het voorbeeld van de basketbal. Stel dat de hoogte van de bal (y) in meters, t seconden nadat hij is gegooid, wordt gegeven door de vergelijking:

y = -5t² + 10t + 2

Hier kunnen we zien dat 'a' -5 is (dus de parabool opent naar beneden), 'b' 10 is en 'c' 2 is.

We kunnen de kwadratische formule gebruiken om te bepalen na hoeveel seconden de bal de grond raakt (wanneer y = 0):

t = (-10 ± √(10² - 4 * -5 * 2)) / (2 * -5)

t = (-10 ± √(140)) / -10

Dit geeft ons twee oplossingen: ongeveer -0.18 en 2.18. Omdat tijd niet negatief kan zijn, is de relevante oplossing 2.18 seconden. Dit betekent dat de bal na ongeveer 2.18 seconden de grond raakt.

De Toekomst van Kwadratische Verbanden

Met de opkomst van data-analyse en machine learning worden kwadratische verbanden steeds belangrijker. Algoritmen gebruiken deze verbanden om patronen te herkennen, voorspellingen te doen en complexe systemen te optimaliseren. Van het voorspellen van aandelenkoersen tot het optimaliseren van de energie-efficiëntie van gebouwen, kwadratische verbanden spelen een cruciale rol in de moderne wereld.

Daarnaast wordt er steeds meer onderzoek gedaan naar het gebruik van kwadratische verbanden in nieuwe technologieën, zoals quantum computing en nanotechnologie. Deze gebieden vereisen een diepgaand begrip van wiskundige modellen om complexe systemen te ontwerpen en te controleren.

Het is dus belangrijk om je wiskundige vaardigheden te blijven ontwikkelen, zodat je kunt profiteren van de mogelijkheden die deze technologieën bieden. De kennis van kwadratische verbanden is een waardevolle investering in je toekomst.

We hebben gezien hoe kwadratische verbanden een krachtige tool zijn om de wereld om ons heen te begrijpen en te voorspellen. Van de baan van een bal tot het ontwerp van een brug, deze verbanden spelen een cruciale rol in verschillende aspecten van ons leven. Hoewel ze misschien complex lijken, zijn ze eigenlijk heel toegankelijk en kunnen ze worden gebruikt om praktische problemen op te lossen.

Hopelijk heeft dit artikel je geholpen om kwadratische verbanden beter te begrijpen en te waarderen. De volgende keer dat je een parabool in de natuur of in een ontwerp ziet, denk dan aan de wiskunde erachter en de mogelijkheden die het biedt.

Ben je nu nieuwsgierig geworden en wil je zelf aan de slag met kwadratische verbanden? Welke real-world situatie zou jij met een kwadratische vergelijking willen modelleren?