Wat Is Een Scherpe Hoek

In de wereld van de wiskunde en de geometrie, komen we verschillende soorten hoeken tegen. Een van de meest fundamentele en eenvoudig te herkennen hoeken is de scherpe hoek. Maar wat is nu precies een scherpe hoek, en waarom is het zo belangrijk om dit concept te begrijpen? In dit artikel duiken we dieper in de definitie, de eigenschappen en de toepassingen van de scherpe hoek, zodat je een helder en compleet beeld krijgt van dit geometrische basisconcept.

Definitie van een Scherpe Hoek

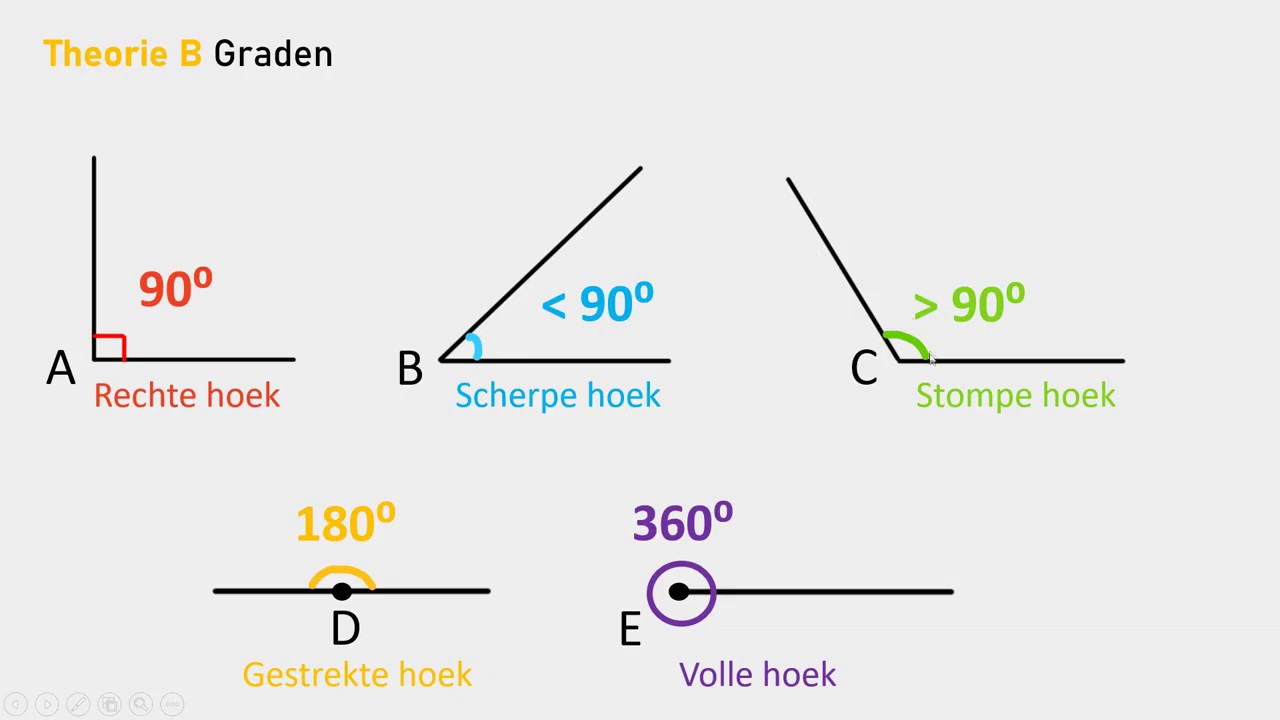
Een scherpe hoek is een hoek die kleiner is dan 90 graden (90°). Dit betekent dat de hoek minder dan een kwart van een volledige cirkel omvat. In geometrische termen wordt een hoek gevormd door twee lijnen of lijnsegmenten die vanuit hetzelfde punt, de hoekpunt, vertrekken. De mate van opening tussen deze twee lijnen bepaalt de grootte van de hoek.

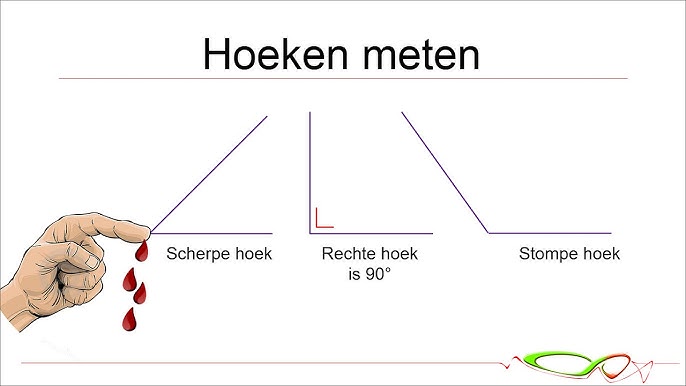
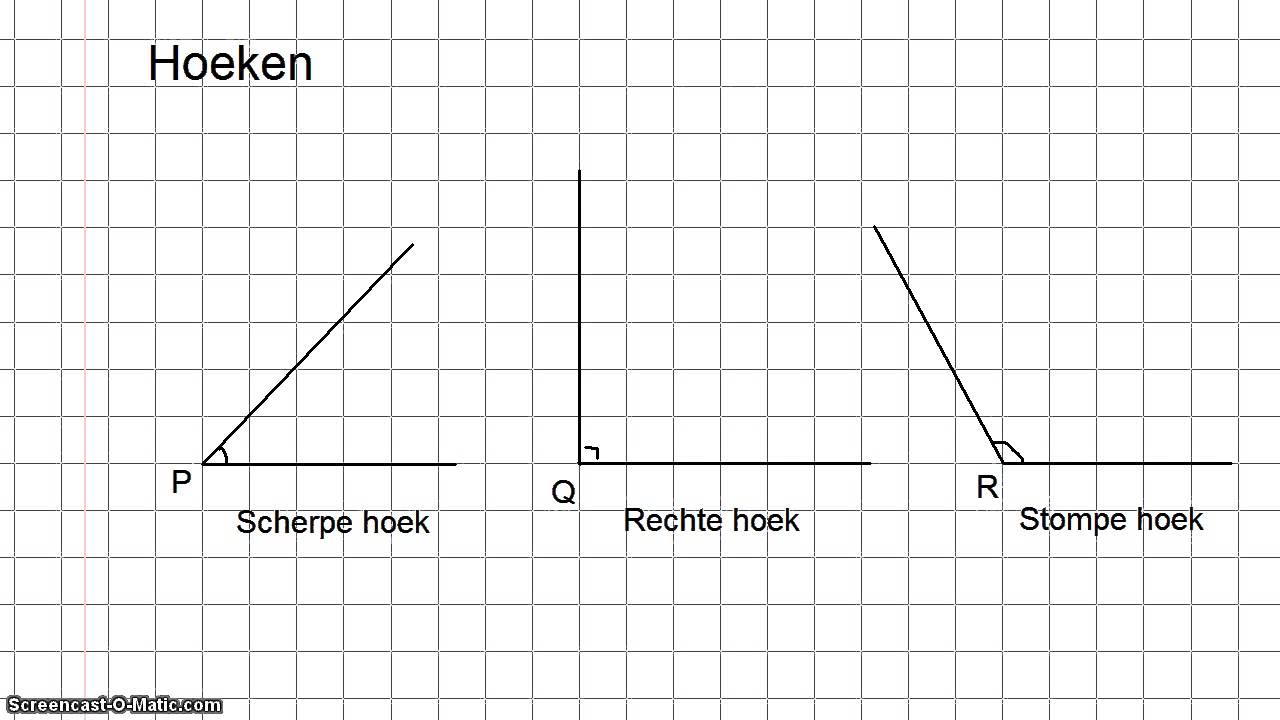
Ter vergelijking: een rechte hoek is precies 90°, een stompe hoek is groter dan 90° maar kleiner dan 180°, en een gestrekte hoek is precies 180°. De scherpe hoek onderscheidt zich dus door zijn beperkte opening en relatief kleine hoekmaat.

Formele Beschrijving

Mathematisch gezien kan een scherpe hoek (θ) worden gedefinieerd als:

0° < θ < 90°

Dit betekent dat de hoekmaat altijd groter moet zijn dan nul graden, maar kleiner dan negentig graden. Een hoek van precies 0° is geen hoek in de gebruikelijke zin, en een hoek van 90° is, zoals eerder vermeld, een rechte hoek.

Eigenschappen van Scherpe Hoeken

Scherpe hoeken hebben een aantal unieke eigenschappen die belangrijk zijn in de geometrie en de trigonometrie. Hieronder staan enkele van de belangrijkste kenmerken:

Complementaire Hoeken

Een scherpe hoek kan een complementaire hoek vormen. Twee hoeken zijn complementair als hun som gelijk is aan 90°. Aangezien een scherpe hoek kleiner is dan 90°, kan hij altijd een andere scherpe hoek complementeren om samen een rechte hoek te vormen.

Bijvoorbeeld, als je een scherpe hoek van 30° hebt, dan is de complementaire hoek 60° (30° + 60° = 90°).

In Driehoeken

Een driehoek kan maximaal drie scherpe hoeken bevatten. Afhankelijk van de andere hoeken in de driehoek, kan de driehoek worden geclassificeerd als een scherphoekige driehoek, een rechthoekige driehoek of een stomphoekige driehoek. Een scherphoekige driehoek heeft drie scherpe hoeken. Een rechthoekige driehoek heeft één rechte hoek en twee scherpe hoeken. Een stomphoekige driehoek heeft één stompe hoek en twee scherpe hoeken.

Het is belangrijk om te onthouden dat de som van de hoeken in een driehoek altijd 180° is. Dit betekent dat als een driehoek een stompe of rechte hoek heeft, de andere twee hoeken noodzakelijkerwijs scherp moeten zijn.

Trigonometrische Functies

In de trigonometrie spelen scherpe hoeken een cruciale rol. De trigonometrische functies zoals sinus (sin), cosinus (cos) en tangens (tan) worden vaak gebruikt om de verhoudingen tussen de zijden van een rechthoekige driehoek te berekenen, waarbij een van de hoeken scherp is.

Voor scherpe hoeken gelden de volgende algemene regels:

• De sinus van een scherpe hoek is altijd positief en kleiner dan 1.
• De cosinus van een scherpe hoek is altijd positief en kleiner dan 1.
• De tangens van een scherpe hoek is altijd positief.

Real-World Voorbeelden van Scherpe Hoeken

Scherpe hoeken kom je overal in het dagelijks leven tegen. Het is nuttig om te leren herkennen, omdat het helpt bij ruimtelijk inzicht en het begrijpen van geometrische vormen.

Architectuur en Design

In de architectuur worden scherpe hoeken vaak gebruikt in de constructie van daken, gevels en andere structurele elementen. Denk bijvoorbeeld aan de scherpe hoek van een puntdak of de hoek die een trap maakt met de vloer. Het ontwerp en de stabiliteit van gebouwen hangen vaak af van de precieze hoekmetingen.

Ook in interieurdesign spelen scherpe hoeken een rol. Meubels, zoals stoelen en tafels, kunnen scherpe hoeken bevatten die zowel esthetisch als functioneel zijn. Hetzelfde geldt voor de hoeken van ramen, deuren en andere architectonische details.

Natuur

Ook in de natuur zijn scherpe hoeken te vinden. De takken van een boom vormen vaak scherpe hoeken met de stam. De hoek van een vogelbek, de vorm van bergen, en de structuren van kristallen laten vaak scherpe hoeken zien. De natuur maakt gebruik van scherpe hoeken voor verschillende doeleinden, van het maximaliseren van blootstelling aan zonlicht tot het creëren van stevige en stabiele structuren.

Techniek en Technologie

In de techniek en technologie worden scherpe hoeken gebruikt in allerlei apparaten en machines. Denk aan de hoek van een schroefdraad, de vorm van een mes, of de hoek van een hellingbaan. De nauwkeurigheid van deze hoeken is vaak cruciaal voor de werking van het apparaat of de machine.

Bijvoorbeeld, in de luchtvaart is de aanvalshoek van een vliegtuigvleugel een scherpe hoek die de lift en de weerstand beïnvloedt. Een juiste aanvalshoek is essentieel voor een veilige en efficiënte vlucht.

Scherpe hoeken in data visualisatie

Data visualisatie maakt vaak gebruik van hoeken in bijvoorbeeld taartdiagrammen. Een taartdiagram gebruikt sectoren, waarvan de hoek aan het middelpunt van de cirkel, een scherpe hoek kan zijn afhankelijk van de percentage van de data die het representeert.

Ook in spreidingsdiagrammen kun je, bij het analyseren van clusters van data punten, indirect kijken naar de hoek die de denkbeeldige lijn die je zou trekken ten opzichte van de x-as maakt. Een scherpe hoek kan hier bijvoorbeeld impliceren dat er een snel toenemende correlatie is tussen twee variabelen in de dataset.

Waarom Scherpe Hoeken Belangrijk Zijn

Het begrijpen van scherpe hoeken is fundamenteel voor het ontwikkelen van een goed ruimtelijk inzicht en het beheersen van de basisprincipes van geometrie. Zonder een solide basis in hoekmetingen en hun eigenschappen is het moeilijk om complexere wiskundige en technische problemen op te lossen. Dit inzicht helpt niet alleen in wiskundige contexten, maar ook in praktische situaties waarin ruimtelijk inzicht vereist is, zoals bij het navigeren, het bouwen van modellen of het ontwerpen van objecten.

Bovendien is het begrip van scherpe hoeken essentieel voor het leren van trigonometrie, een tak van de wiskunde die cruciaal is voor veel wetenschappelijke en technische disciplines. Van de berekening van de hoogte van een gebouw tot het modelleren van de beweging van een projectiel, trigonometrische functies worden overal gebruikt waar hoeken en afstanden een rol spelen.

Door de basisprincipes van scherpe hoeken te begrijpen, leg je een solide basis voor verdere studie en toepassing in een breed scala aan gebieden.

Conclusie

Een scherpe hoek is een hoek kleiner dan 90°, en het is een fundamenteel concept in de geometrie en daarbuiten. We hebben gekeken naar de definitie, de eigenschappen, en talloze voorbeelden uit het dagelijks leven, de natuur, en de technologie. Het begrijpen van scherpe hoeken is niet alleen belangrijk voor wiskundige vaardigheden, maar ook voor het ontwikkelen van ruimtelijk inzicht en het begrijpen van de wereld om ons heen.

Dus, de volgende keer dat je een scherpe hoek tegenkomt, of het nu in een gebouw, een boom, of een machine is, neem dan even de tijd om erover na te denken en de wiskundige principes te waarderen die eraan ten grondslag liggen. Daag jezelf uit om scherpe hoeken te herkennen en hun eigenschappen te analyseren. Door actief te oefenen en je kennis toe te passen, kun je je ruimtelijk inzicht en wiskundige vaardigheden verder ontwikkelen.