Wilcoxon Signed Rank Sum Test

Laten we eerlijk zijn, statistiek kan soms aanvoelen als een mijnenveld. Je bent bezig met je onderzoek, verzamelt data en probeert chocola te maken van al die cijfers. En dan kom je een test tegen die je nog niet kent, zoals de Wilcoxon Signed Rank Sum Test. Geen paniek! Dit artikel is geschreven om je te helpen deze test te begrijpen en toe te passen, zodat je met vertrouwen conclusies kunt trekken uit je data.

Waarom is dit belangrijk? Omdat statistische tests, zoals de Wilcoxon test, een cruciale rol spelen in onderzoek in vrijwel elk veld. Of je nu een psycholoog bent die de effectiviteit van een therapie onderzoekt, een econoom die de impact van een nieuw beleid analyseert, of een bioloog die de groei van planten onderzoekt, de juiste statistische test kan je helpen objectieve en betrouwbare conclusies te trekken.

Wat is de Wilcoxon Signed Rank Sum Test?

De Wilcoxon Signed Rank Sum Test, ook wel de Wilcoxon tekentoets genoemd, is een niet-parametrische statistische test. Dit betekent dat de test geen aannames maakt over de verdeling van de data, in tegenstelling tot parametrische tests zoals de t-test. Dit is vooral handig als je data niet normaal verdeeld is, wat in de praktijk vaak voorkomt. Stel je voor dat je de pijnscore van patiënten voor en na een behandeling meet. De pijnscore is subjectief en vaak niet normaal verdeeld, hier is de Wilcoxon test dus erg nuttig!

Wanneer gebruik je de Wilcoxon test?

De Wilcoxon Signed Rank Sum Test is ideaal voor:

Gepaarde data: Je hebt twee sets data die aan elkaar gerelateerd zijn. Denk aan metingen van dezelfde persoon (voor en na een interventie), dezelfde locatie (verschillende tijdstippen), of vergelijkbare objecten (twee helften van een blad).
Niet-normale verdeling: Je data is niet normaal verdeeld, of je bent er niet zeker van of dit het geval is.
Ordinale data: Je data is op een ordinale schaal gemeten (zoals rangordes, Likert-schalen). Hoewel de test ook op interval of ratio data toegepast kan worden, is hij vooral waardevol wanneer de aannames voor parametrische tests niet voldaan wordt.

Wat doet de test eigenlijk?

In essentie vergelijkt de Wilcoxon test de mediaan van de verschillen tussen de gepaarde metingen met nul. De test kijkt niet alleen naar de grootte van de verschillen, maar ook naar de richting (positief of negatief). Vervolgens worden de verschillen in absolute waarde gerangschikt, waarbij de kleinste absolute verschil de rang 1 krijgt. Positieve en negatieve rangen worden vervolgens afzonderlijk opgeteld. De teststatistiek is de kleinste van deze twee sommen. Een kleine teststatistiek duidt op een significant verschil tussen de twee groepen.

Denk hierbij aan een wedstrijd tussen twee teams waarbij je de individuele prestaties van elke speler in beide teams vergelijkt. De Wilcoxon test vergelijkt dan of de speler van team A systematisch beter (of slechter) presteert dan dezelfde speler van team B, rekening houdend met de grootte van het verschil.

Hoe werkt de Wilcoxon Signed Rank Sum Test? Een stapsgewijze uitleg

Laten we de stappen van de Wilcoxon Signed Rank Sum Test eens doornemen met een voorbeeld. Stel, je wilt onderzoeken of een nieuwe trainingsmethode de hardlooptijd van atleten verbetert. Je meet de tijd van 10 atleten voor en na de training:

Bereken de verschillen: Trek voor elke atleet de tijd na de training af van de tijd voor de training. Als de tijd na de training lager is, is het verschil positief (een verbetering).
Negeer verschillen van nul: Als een atleet dezelfde tijd heeft gelopen, laat je die observatie weg uit de analyse.
Rangschik de absolute waarden van de verschillen: Geef de kleinste absolute verschil rang 1, de op een na kleinste rang 2, enzovoort. Als er gelijke verschillen zijn (ties), geef ze allemaal de gemiddelde rang van de rangen die ze zouden hebben gekregen als ze niet gelijk waren.
Ken de rangen het teken toe van het oorspronkelijke verschil: Als het verschil positief was, behoud je de positieve rang. Als het verschil negatief was, maak je de rang negatief.
Bereken de som van de positieve rangen (W+) en de som van de negatieve rangen (W-): Dit zijn je twee belangrijkste teststatistieken.
Bereken de teststatistiek (W): De teststatistiek W is de kleinste van W+ en W-.
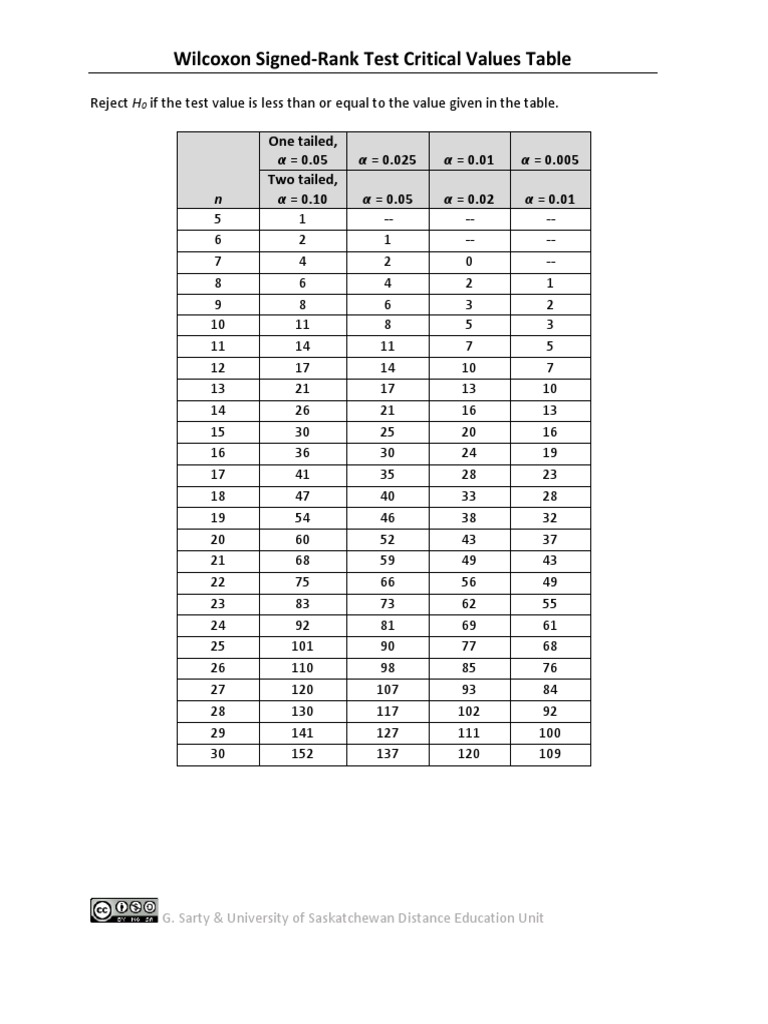
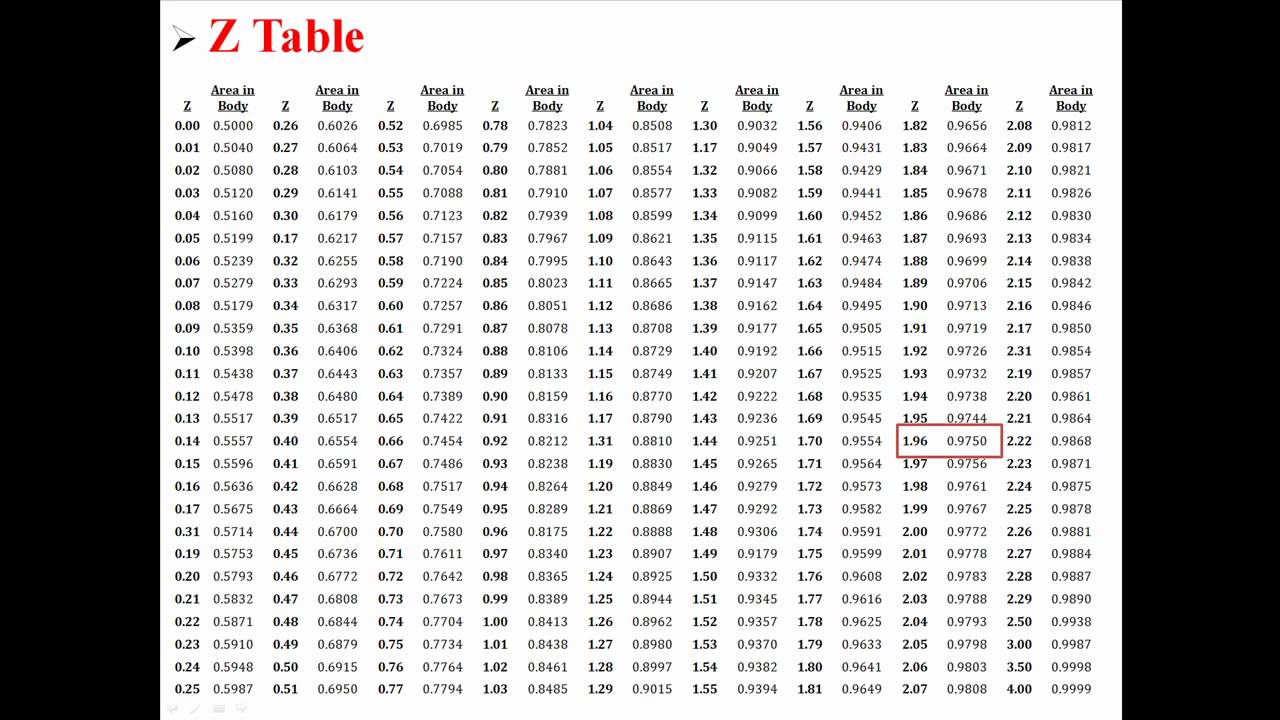
Vergelijk de teststatistiek met een kritieke waarde: Gebruik een tabel of een statistisch programma om de p-waarde te bepalen die overeenkomt met jouw teststatistiek en steekproefomvang.
Trek een conclusie: Als de p-waarde kleiner is dan je significantieniveau (meestal 0.05), verwerp je de nulhypothese en concludeer je dat er een significant verschil is tussen de twee groepen.

Een voorbeeld:

Stel dat na de bovenstaande stappen W+ = 45 en W- = 10. Dan is de teststatistiek W = 10. Je vergelijkt deze waarde met een kritieke waarde (of berekent de p-waarde) om te bepalen of het verschil significant is. Als de p-waarde kleiner is dan 0.05, dan is er een significant verschil en kun je concluderen dat de trainingsmethode de hardlooptijd significant heeft verbeterd.

Waarom zou je de Wilcoxon test gebruiken in plaats van een t-test?

De t-test is een krachtige statistische test, maar hij heeft een belangrijke aanname: de data moet normaal verdeeld zijn. Als je data niet normaal verdeeld is, kan de t-test onbetrouwbare resultaten opleveren. De Wilcoxon test daarentegen, is robuuster en minder gevoelig voor afwijkingen van de normale verdeling. Dit maakt de Wilcoxon test een betere keuze wanneer je twijfelt over de normaliteit van je data, of wanneer je data ordinaal is.

Counterpoints: De nadelen van de Wilcoxon test

Hoewel de Wilcoxon test een waardevol instrument is, is het belangrijk om te erkennen dat er ook nadelen zijn:

Minder power: In sommige gevallen, wanneer de data wel normaal verdeeld is, heeft de Wilcoxon test minder statistische power dan de t-test. Dit betekent dat de Wilcoxon test minder snel een significant verschil zal detecteren als het er daadwerkelijk is.
Minder informatie: De Wilcoxon test maakt gebruik van de rangordes van de verschillen, niet de exacte waarden. Hierdoor gaat er informatie verloren die wel gebruikt wordt in de t-test.
Complexere berekeningen met veel ties: Hoewel statistische software dit voor je oplost, kunnen de berekeningen bij veel gelijke verschillen ingewikkelder worden.

Het is dus belangrijk om de voor- en nadelen van beide tests af te wegen voordat je een keuze maakt.

Praktische Toepassingen: Voorbeelden uit het echte leven

De Wilcoxon test is niet alleen een theoretisch concept. Hier zijn een paar voorbeelden van hoe deze test in de praktijk wordt toegepast:

Geneeskunde: Het vergelijken van de pijnscore van patiënten voor en na een behandeling, zoals in de eerder genoemde pijnbehandeling.
Psychologie: Het evalueren van de effectiviteit van een therapie door het meten van de symptomen van deelnemers voor en na de therapie.
Marketing: Het testen van de impact van een nieuwe advertentiecampagne door het meten van de merkbekendheid voor en na de campagne.
Onderwijs: Het vergelijken van de prestaties van studenten op een toets voor en na een bepaalde lesmethode.
Ecologie: Onderzoek naar de hoeveelheid van een vervuilende stof in een bepaald gebied voor en na een schoonmaakactie.

Deze voorbeelden laten zien dat de Wilcoxon test een veelzijdig instrument is dat in diverse disciplines kan worden gebruikt om veranderingen te meten en te evalueren.

Conclusie

De Wilcoxon Signed Rank Sum Test is een waardevol alternatief voor de t-test wanneer je data niet normaal verdeeld is of wanneer je werkt met ordinale data. Het is een relatief eenvoudige test om te begrijpen en toe te passen, en het kan je helpen om betrouwbare conclusies te trekken uit je data. Hoewel de test enkele nadelen heeft, is hij in veel situaties een betere keuze dan de t-test. Het is belangrijk om te onthouden dat de keuze van de juiste statistische test afhangt van de specifieke kenmerken van je data en je onderzoeksvraag. Wees kritisch en denk goed na over welke test het meest geschikt is voor jouw situatie.

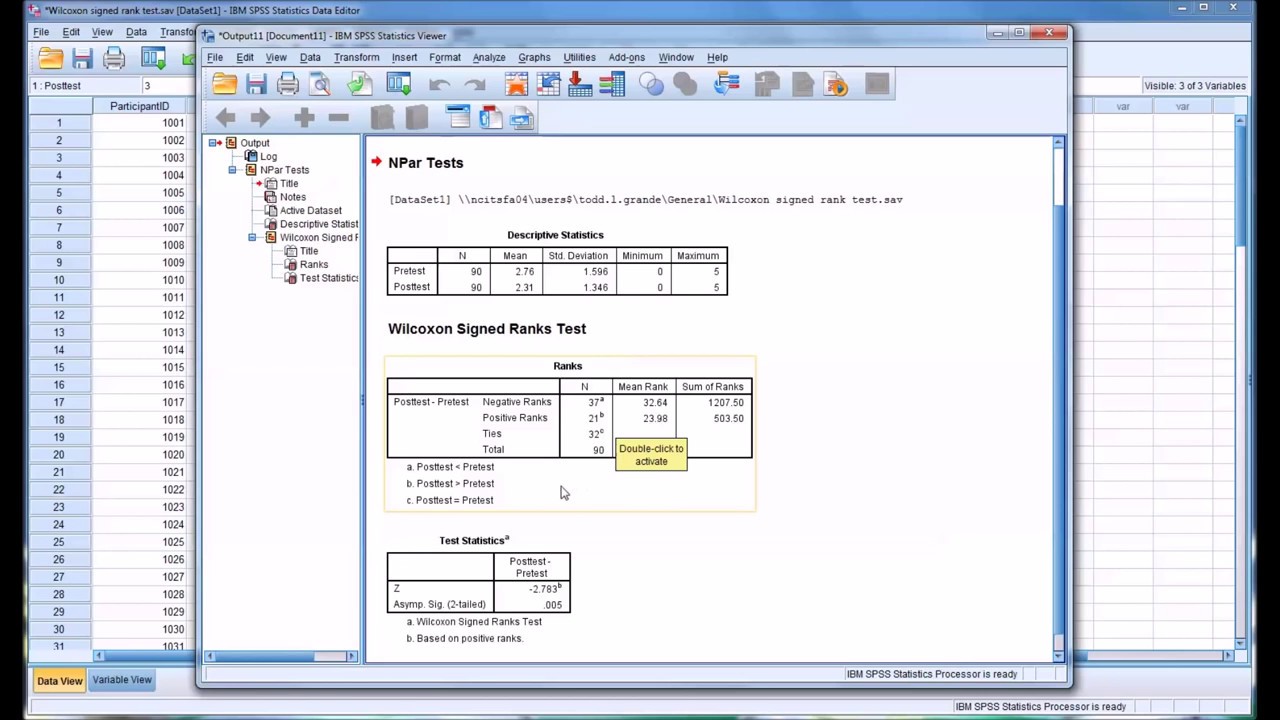
Wees niet bang om deze test in de praktijk te brengen. Er zijn tal van statistische softwarepakketten (zoals SPSS, R, en Python) die de Wilcoxon test voor je kunnen uitvoeren. Experimenteer met verschillende datasets en oefen met het interpreteren van de resultaten. Hoe meer je oefent, hoe comfortabeler je zult worden met het gebruik van deze krachtige statistische tool.

Met deze kennis op zak, voel je je nu beter in staat om de Wilcoxon Signed Rank Sum Test toe te passen in je eigen onderzoek? Welke concrete stappen ga je nu zetten om de Wilcoxon Signed Rank Sum Test beter te leren kennen en in je werk te integreren?