De Grafiek En De Vergelijking Van Een Lineaire Functie

Heb je ooit het gevoel gehad dat wiskunde een abstracte wereld is, losgekoppeld van de realiteit? Veel mensen worstelen met concepten zoals lineaire functies, vooral als ze de grafieken en vergelijkingen ervan proberen te begrijpen. Het voelt misschien alsof je je tijd verdoet met het leren van iets dat nooit van pas zal komen. Maar wat als ik je zou vertellen dat lineaire functies overal om ons heen zijn, en dat het begrijpen ervan je kan helpen om de wereld beter te begrijpen?

Laten we eerlijk zijn, wiskunde kan intimiderend zijn. De formules, de variabelen, de ingewikkelde grafieken… het kan overweldigend zijn. Je bent niet de enige die moeite heeft om de verbinding te leggen tussen de theorie en de praktijk. Misschien heb je wiskunde zelfs wel helemaal opgegeven, in de overtuiging dat het gewoon niets voor jou is. Maar ik ben hier om je te vertellen dat iedereen lineaire functies kan begrijpen, met de juiste uitleg en een beetje geduld.

De Impact van Lineaire Functies in het Dagelijks Leven

Lineaire functies zijn veel meer dan alleen maar formules op papier. Ze zijn een krachtig hulpmiddel om relaties tussen verschillende variabelen te modelleren en te voorspellen. Denk aan de volgende voorbeelden:

Benzineprijs: Stel dat de benzineprijs per liter een vast bedrag per week stijgt. De totale kosten van benzine kunnen dan worden gemodelleerd met een lineaire functie.
Telefoonabonnement: Veel telefoonabonnementen hebben een vaste maandelijkse prijs plus een bedrag per verbruikte data. Ook dit is een voorbeeld van een lineaire functie.
Snelheid en Afstand: Als je met een constante snelheid reist, is de afgelegde afstand een lineaire functie van de tijd.
Koken: Het omrekenen van temperaturen van Celsius naar Fahrenheit is een lineair verband.
Financiën: Een lening met een vaste rente kan lineair worden gemodelleerd over een korte periode.

Zoals je ziet, zijn lineaire functies relevant voor allerlei aspecten van ons leven. Door ze te begrijpen, kunnen we betere beslissingen nemen en de wereld om ons heen beter interpreteren.

Wat Is een Lineaire Functie Eigenlijk?

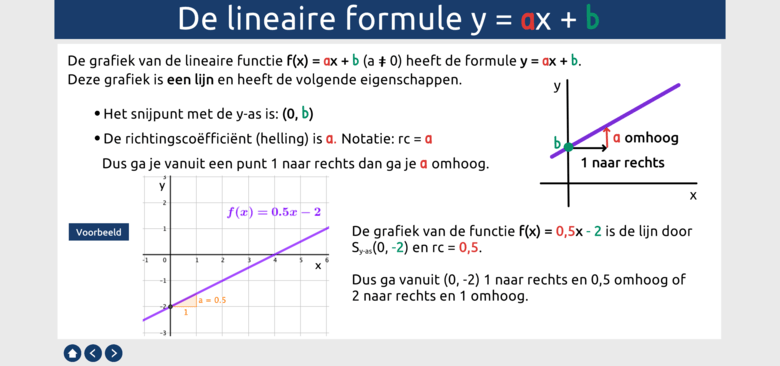
Een lineaire functie is een wiskundige relatie tussen twee variabelen waarbij de grafiek een rechte lijn vormt. De algemene vorm van een lineaire functie is:

y = mx + b

Waarbij:

y de afhankelijke variabele is (de waarde die verandert als gevolg van de waarde van x).
x de onafhankelijke variabele is (de waarde die je zelf kunt kiezen).
m de richtingscoëfficiënt is (de helling van de lijn, die aangeeft hoeveel y verandert voor elke eenheid dat x verandert).
b het snijpunt met de y-as is (de waarde van y wanneer x gelijk is aan 0).

Laten we dit eens bekijken met een eenvoudig voorbeeld: y = 2x + 1

In dit geval is m = 2, wat betekent dat voor elke 1 die x toeneemt, y met 2 toeneemt. b = 1, wat betekent dat de lijn de y-as snijdt bij het punt (0, 1).

De Grafiek van een Lineaire Functie

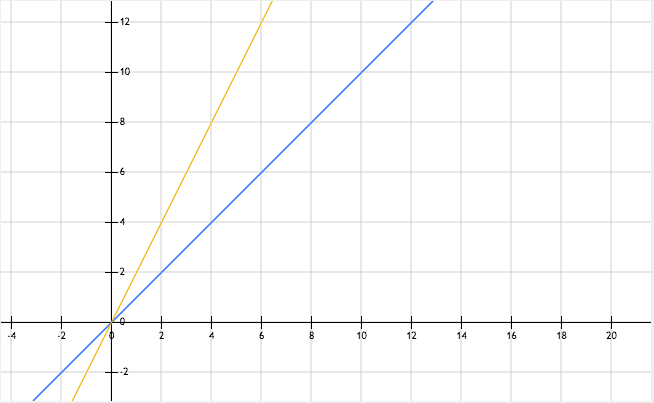
De grafiek van een lineaire functie is een rechte lijn. Om de grafiek te tekenen, heb je minstens twee punten nodig. Deze punten kun je vinden door verschillende waarden voor x te kiezen en de bijbehorende waarden voor y te berekenen met behulp van de vergelijking.

Laten we teruggaan naar ons voorbeeld: y = 2x + 1

Als we x = 0 invullen, krijgen we y = 2(0) + 1 = 1. Dus het punt (0, 1) ligt op de grafiek.

Als we x = 1 invullen, krijgen we y = 2(1) + 1 = 3. Dus het punt (1, 3) ligt ook op de grafiek.

Nu kun je deze twee punten (0, 1) en (1, 3) op een grafiek uitzetten en een rechte lijn trekken die door beide punten gaat. Dit is de grafiek van de lineaire functie y = 2x + 1.

De Richtingscoëfficiënt (m)

De richtingscoëfficiënt (m) is een cruciaal element van een lineaire functie. Het geeft aan hoe steil de lijn is en of de lijn stijgend of dalend is.

Als m positief is, stijgt de lijn van links naar rechts. Hoe groter de waarde van m, hoe steiler de lijn.
Als m negatief is, daalt de lijn van links naar rechts. Hoe kleiner de waarde van m (d.w.z. hoe groter de absolute waarde van m), hoe steiler de lijn.
Als m gelijk is aan 0, is de lijn horizontaal.

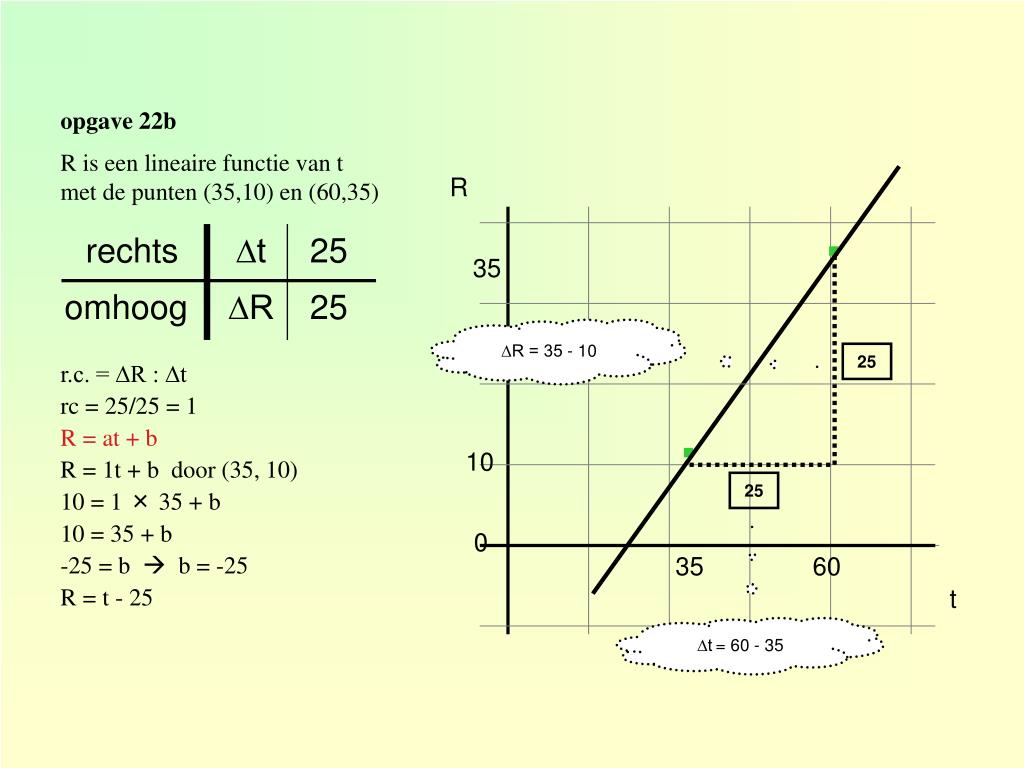
Je kunt de richtingscoëfficiënt berekenen als je twee punten op de lijn kent, bijvoorbeeld (x1, y1) en (x2, y2):

m = (y2 - y1) / (x2 - x1)

Het Snijpunt met de y-as (b)

Het snijpunt met de y-as (b) is het punt waar de lijn de y-as snijdt. Dit is de waarde van y wanneer x gelijk is aan 0. Het snijpunt met de y-as geeft aan waar de lijn begint op de y-as.

Counterpoints: Waarom Sommigen Lineaire Functies Als Irrelevant Beschouwen

Het is begrijpelijk dat sommige mensen lineaire functies als irrelevant beschouwen. Sommige argumenten zijn:

De realiteit is zelden perfect lineair: Veel real-world scenario's zijn complexer dan een eenvoudige lineaire functie. Factoren zoals variabele kosten, externe invloeden en niet-lineaire relaties kunnen de uitkomst beïnvloeden.
Alternatieve wiskundige modellen zijn beter geschikt: Voor complexe situaties zijn er meer geavanceerde wiskundige modellen beschikbaar, zoals exponentiële functies, polynomiale functies en statistische modellen.
De focus op abstractie kan verwarrend zijn: Voor sommige leerlingen kan de nadruk op abstracte vergelijkingen en grafieken leiden tot verwarring en desinteresse, omdat ze de concrete toepassingen niet zien.

Hoewel deze argumenten valide zijn, is het belangrijk om te onthouden dat lineaire functies een fundamenteel concept zijn in de wiskunde. Ze vormen de basis voor meer complexe modellen en bieden een nuttige benadering van vele real-world situaties. Bovendien is het begrijpen van lineaire functies een uitstekende oefening in logisch denken en probleemoplossing.

Oplossingsgericht: Hoe Lineaire Functies Makkelijker te Begrijpen

Hier zijn enkele tips om lineaire functies beter te begrijpen:

Begin met concrete voorbeelden: Zoek voorbeelden in je eigen leven waar lineaire relaties voorkomen. Denk aan de kosten van een taxi, de opbrengst van zonnepanelen, of het aantal calorieën dat je verbrandt tijdens het sporten.
Gebruik visuele hulpmiddelen: Teken zelf grafieken van lineaire functies met behulp van een grafische rekenmachine of online tools. Experimenteer met verschillende waarden voor m en b om te zien hoe de grafiek verandert.
Oefen, oefen, oefen: Maak zoveel mogelijk oefenopgaven om je vaardigheden te verbeteren. Begin met eenvoudige opgaven en werk geleidelijk toe naar complexere problemen.
Zoek hulp als je vastloopt: Aarzel niet om hulp te vragen aan je docent, medestudenten, of online forums. Er zijn talloze bronnen beschikbaar om je te helpen lineaire functies te begrijpen.
Bekijk het als een puzzel: Probeer het leren van lineaire functies te benaderen als een puzzel. Het is een kwestie van logisch nadenken en de juiste stukjes (de formules en definities) op de juiste plaats leggen.
Realiseer je dat het tijd kost: Het kost tijd en moeite om lineaire functies volledig te begrijpen. Wees geduldig met jezelf en geef niet op als je het niet meteen snapt.

Conclusie

Lineaire functies zijn een essentieel onderdeel van de wiskunde en hebben een grote impact op ons dagelijks leven. Hoewel het begrijpen van de grafiek en de vergelijking in eerste instantie misschien lastig lijkt, is het zeker haalbaar met de juiste aanpak en wat oefening. Door de relevantie van lineaire functies te erkennen en concrete voorbeelden te gebruiken, kun je de abstractie doorbreken en de schoonheid van deze wiskundige relatie ontdekken.

Ben je nu geïnspireerd om de relatie tussen grafieken en vergelijkingen van lineaire functies verder te onderzoeken en te ontdekken hoe ze in jouw leven een rol spelen?