Formules Herleiden Wiskunde A Havo 5

Zit je in 5 Havo en worstel je met het herleiden van formules bij Wiskunde A? Je bent zeker niet de enige! Veel leerlingen vinden dit een lastig onderdeel, maar met de juiste aanpak en een beetje oefening kan je dit zeker onder de knie krijgen. Deze handleiding is speciaal voor jou gemaakt, om je stap voor stap door de basisprincipes en veelvoorkomende technieken van het herleiden van formules te loodsen. We gaan in op de waarom, de hoe en de waarvoor, zodat je niet alleen weet hoe je een formule moet herleiden, maar ook begrijpt waarom je het doet.

Waarom Formules Herleiden Belangrijk Is

Voordat we de diepte induiken, laten we even stilstaan bij de essentie. Waarom is het herleiden van formules zo'n belangrijk onderdeel van Wiskunde A? Het antwoord is simpel: het stelt je in staat om problemen op te lossen, verbanden te leggen en inzicht te krijgen in de wereld om je heen.

Problemen oplossen: In veel praktische situaties krijg je een formule aangereikt die net niet de variabele geeft die je zoekt. Door de formule te herleiden, kun je deze aanpassen zodat je direct de gewenste waarde kunt berekenen. Denk aan het berekenen van de benodigde rentevoet om een bepaald bedrag te sparen in een bepaalde tijd, of het bepalen van de afstand die je moet afleggen bij een bepaalde snelheid en reistijd.
Verbanden leggen: Het herleiden van formules laat zien hoe verschillende variabelen met elkaar samenhangen. Je ziet hoe een verandering in de ene variabele een effect heeft op de andere. Dit helpt je om de onderliggende principes van een formule te begrijpen en te voorspellen hoe een systeem zich zal gedragen.
Inzicht krijgen: Door formules te herleiden, krijg je een dieper inzicht in de betekenis van de formule en de variabelen die erin voorkomen. Je leert de structuur van de formule herkennen en begrijpen, wat het makkelijker maakt om complexere problemen aan te pakken.

Kortom, het herleiden van formules is een essentiële vaardigheid die je helpt om wiskundige problemen te analyseren en op te lossen, verbanden te leggen en inzicht te krijgen in de wereld om je heen. Zonder deze vaardigheid ben je eigenlijk beperkt tot het simpelweg invullen van getallen in een bestaande formule, zonder echt te begrijpen wat er gebeurt.

De Basisprincipes van Formules Herleiden

Het herleiden van formules draait om het manipuleren van een formule om een bepaalde variabele vrij te maken, ofwel, om de formule te schrijven in een andere vorm waarin de gewenste variabele geïsoleerd staat aan één kant van het isgelijkteken. Dit doe je door gebruik te maken van een aantal basisprincipes van de algebra. De belangrijkste principes zijn:

Gelijkheidsprincipe

Het belangrijkste principe is dat je beide kanten van de vergelijking gelijk moet behandelen. Wat je aan de ene kant doet, moet je ook aan de andere kant doen. Dit zorgt ervoor dat de vergelijking in balans blijft en de relatie tussen de variabelen niet verandert.

Optellen en aftrekken: Je mag aan beide kanten van de vergelijking hetzelfde getal of dezelfde term optellen of aftrekken. Bijvoorbeeld, als je de vergelijking x + 3 = 5 hebt, kun je aan beide kanten 3 aftrekken om x vrij te maken: x + 3 - 3 = 5 - 3, wat resulteert in x = 2.
Vermenigvuldigen en delen: Je mag beide kanten van de vergelijking vermenigvuldigen of delen door hetzelfde getal (behalve 0). Bijvoorbeeld, als je de vergelijking 2x = 6 hebt, kun je beide kanten delen door 2 om x vrij te maken: 2x / 2 = 6 / 2, wat resulteert in x = 3.

Omgekeerde bewerkingen

Om een variabele vrij te maken, gebruik je omgekeerde bewerkingen. Dit betekent dat je de bewerking die op de variabele wordt uitgevoerd ongedaan maakt. De omgekeerde bewerkingen zijn:

Optellen en aftrekken zijn elkaars omgekeerde.
Vermenigvuldigen en delen zijn elkaars omgekeerde.
Kwadraat en worteltrekken zijn elkaars omgekeerde.

Bijvoorbeeld, als x wordt vermenigvuldigd met 3 (3x), dan deel je beide kanten door 3 om de 3 te verwijderen. Als x in het kwadraat staat (x²), dan trek je de wortel uit beide kanten om de kwadraat te verwijderen.

Volgorde van bewerkingen

Bij het herleiden van formules is het belangrijk om de volgorde van bewerkingen in acht te nemen. De bekende regel "Meneer Van Dalen Wacht Op Antwoord" (Machtsverheffen, Vermenigvuldigen, Delen, Worteltrekken, Optellen, Aftrekken) helpt je hierbij. Bij het herleiden van een formule werk je deze volgorde in omgekeerde richting af. Dus eerst optellen en aftrekken, dan vermenigvuldigen en delen, enzovoort.

Stappenplan voor het Herleiden van Formules

Om het herleiden van formules makkelijker te maken, kun je het volgende stappenplan volgen:

Identificeer de variabele die je wilt vrijmaken. Welke variabele wil je isoleren aan één kant van de vergelijking?
Kijk welke bewerkingen op de variabele worden uitgevoerd. Wordt de variabele vermenigvuldigd, gedeeld, opgeteld, afgetrokken, gekwadrateerd, of staat hij onder een wortel?
Gebruik de omgekeerde bewerkingen om de variabele vrij te maken. Voer de omgekeerde bewerking uit op beide kanten van de vergelijking.
Houd de volgorde van bewerkingen in de gaten (in omgekeerde richting). Werk van buiten naar binnen, beginnend met optellen en aftrekken, en eindigend met machtsverheffen en worteltrekken.
Vereenvoudig de formule indien mogelijk. Combineer gelijke termen en vereenvoudig breuken.

Voorbeelden van Formules Herleiden

Laten we een paar voorbeelden bekijken om het stappenplan in actie te zien.

Voorbeeld 1: Herleiden van de formule voor afstand (s), snelheid (v) en tijd (t)

De formule voor afstand is: s = v * t. Stel dat we de formule willen herleiden om de snelheid (v) uit te drukken in termen van afstand (s) en tijd (t).

We willen v vrijmaken.
v wordt vermenigvuldigd met t.
De omgekeerde bewerking van vermenigvuldigen is delen. We delen beide kanten van de vergelijking door t: s / t = (v * t) / t.
Vereenvoudig: s / t = v.

De herleide formule is: v = s / t. Dit betekent dat je de snelheid kunt berekenen door de afstand te delen door de tijd.

Voorbeeld 2: Herleiden van de formule voor de oppervlakte van een cirkel

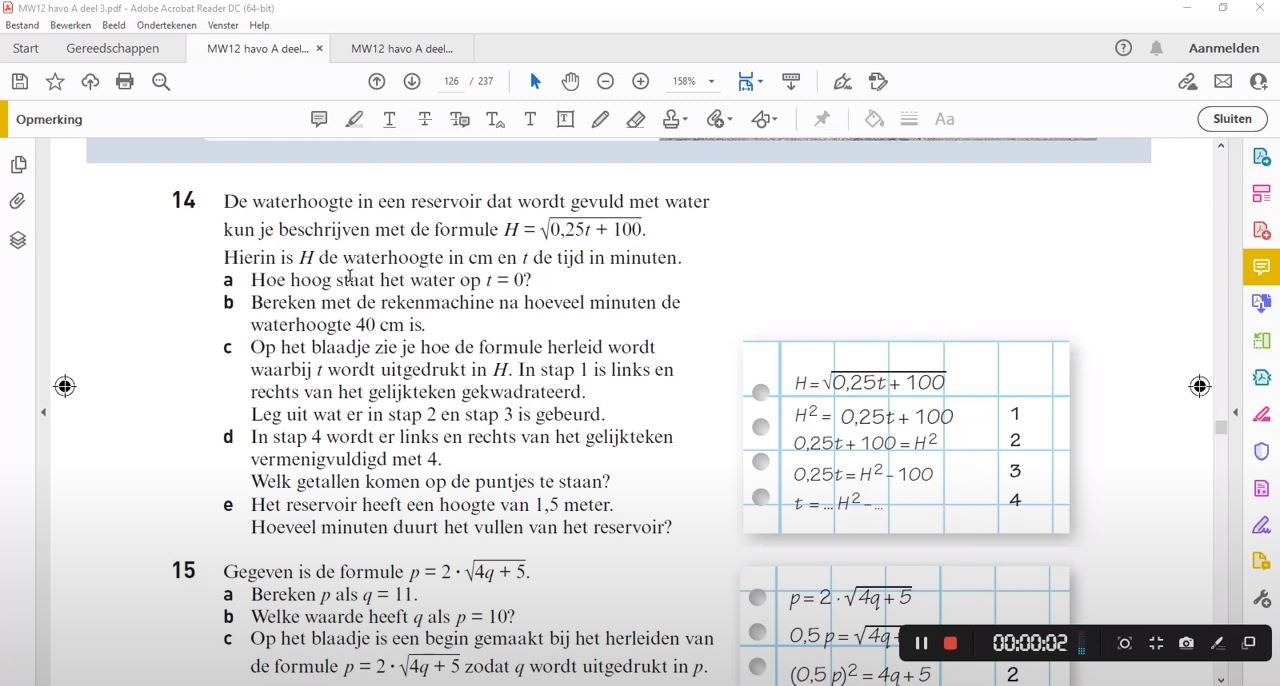
De formule voor de oppervlakte van een cirkel is: A = π * r², waarbij A de oppervlakte is, π (pi) een constante is (ongeveer 3,14) en r de straal is. Stel dat we de formule willen herleiden om de straal (r) uit te drukken in termen van de oppervlakte (A).

We willen r vrijmaken.
r staat in het kwadraat en wordt vermenigvuldigd met π.
Eerst delen we beide kanten van de vergelijking door π: A / π = (π * r²) / π.
Vereenvoudig: A / π = r².
Nu trekken we de wortel uit beide kanten van de vergelijking: √(A / π) = √(r²).
Vereenvoudig: √(A / π) = r.

De herleide formule is: r = √(A / π). Dit betekent dat je de straal kunt berekenen door de wortel te trekken uit de oppervlakte gedeeld door pi.

Voorbeeld 3: Een complexere formule

Stel, je hebt de formule y = 2x + 5 en je wilt x uitdrukken in termen van y.

We willen x vrijmaken.
x wordt vermenigvuldigd met 2 en er wordt 5 bij opgeteld.
Eerst trekken we 5 af van beide kanten: y - 5 = 2x + 5 - 5.
Vereenvoudig: y - 5 = 2x.
Nu delen we beide kanten door 2: (y - 5) / 2 = 2x / 2.
Vereenvoudig: (y - 5) / 2 = x.

De herleide formule is: x = (y - 5) / 2.

Tips & Tricks voor het Herleiden van Formules

Schrijf elke stap op. Het is verleidelijk om stappen over te slaan, maar dit vergroot de kans op fouten. Door elke stap op te schrijven, houd je overzicht en kun je makkelijker controleren of je geen fouten hebt gemaakt.
Controleer je antwoord. Vul je antwoord in de oorspronkelijke formule in om te kijken of het klopt. Als de vergelijking niet klopt, heb je ergens een fout gemaakt.
Oefen, oefen, oefen! Hoe meer je oefent, hoe beter je wordt in het herleiden van formules. Maak opgaven uit je leerboek, zoek online naar oefenopgaven, of vraag je docent om extra oefenmateriaal.
Wees geduldig. Het herleiden van formules kan soms lastig zijn, vooral bij complexere formules. Geef niet op als het niet meteen lukt. Neem de tijd, denk goed na over de stappen die je moet zetten, en probeer het opnieuw.
Begrijp de betekenis van de formules. Het helpt enorm als je weet wat de formule betekent en welke verbanden er zijn tussen de verschillende variabelen. Dit maakt het makkelijker om de juiste stappen te zetten bij het herleiden.

Veelgemaakte Fouten bij het Herleiden van Formules

Hier zijn een paar veelgemaakte fouten die je moet vermijden:

Vergeten om beide kanten van de vergelijking hetzelfde te behandelen. Dit is de meest voorkomende fout. Onthoud altijd dat je elke bewerking die je aan de ene kant van de vergelijking uitvoert, ook aan de andere kant moet uitvoeren.
De volgorde van bewerkingen verkeerd toepassen. Zorg ervoor dat je de volgorde van bewerkingen (Meneer Van Dalen Wacht Op Antwoord in omgekeerde volgorde) correct toepast.
Verkeerde omgekeerde bewerkingen gebruiken. Gebruik de juiste omgekeerde bewerking om de variabele vrij te maken. Optellen en aftrekken zijn elkaars omgekeerde, vermenigvuldigen en delen zijn elkaars omgekeerde, en kwadraat en worteltrekken zijn elkaars omgekeerde.
Slordig werken. Schrijf elke stap op en controleer je werk zorgvuldig. Slordigheid kan leiden tot onnodige fouten.

Waarom Lukt Het Niet Altijd?

Soms lukt het gewoon niet, ondanks al je inspanningen. Dat is oké! Het kan zijn dat de formule te complex is, of dat je een bepaald concept nog niet helemaal begrijpt. In dat geval is het belangrijk om hulp te vragen. Ga naar je docent, een klasgenoot, of zoek online naar uitleg en voorbeelden. Er zijn genoeg bronnen beschikbaar om je te helpen.

Oefenen Baart Kunst

Onthoud: oefening baart kunst. Hoe meer je oefent met het herleiden van formules, hoe beter je erin wordt. Blijf oefenen, wees geduldig, en geef niet op! Met de juiste aanpak en een beetje doorzettingsvermogen kun je dit zeker onder de knie krijgen.

Succes met het herleiden van formules! Hopelijk heeft dit artikel je geholpen om de basisprincipes en technieken beter te begrijpen. Onthoud de stappen, vermijd de veelgemaakte fouten, en blijf oefenen. Voor je het weet, ben jij een expert in het herleiden van formules!