Graden Van Een Hoek Berekenen

We kennen het allemaal wel: je zit in de tuin, probeert een constructie te maken, of misschien wel een wiskundesom op te lossen, en je stuit op de vraag: "Hoe bereken ik nu precies de graden van deze hoek?" Het kan frustrerend zijn, zeker als je het gevoel hebt dat je de basisprincipes niet helemaal onder de knie hebt. Geen zorgen, je bent niet de enige! Velen worstelen met geometrie, en het berekenen van hoeken is een cruciaal onderdeel ervan.

Dit artikel is geschreven om je te helpen. We begrijpen dat wiskunde soms intimiderend kan zijn, en we zullen daarom proberen alles zo helder en begrijpelijk mogelijk uit te leggen. We focussen ons niet alleen op de theorie, maar ook op de praktische toepassing, zodat je direct kunt zien hoe deze kennis je kan helpen in de echte wereld.

Waarom is het Berekenen van Hoekgraden Belangrijk?

Misschien vraag je je af: "Waarom zou ik me hier druk om maken? Ik ben geen architect of ingenieur." Toch is het berekenen van hoekgraden relevanter dan je denkt. Denk bijvoorbeeld aan:

• Klusprojecten in huis: Een plank recht ophangen, een schilderij in de juiste hoek, of zelfs het in elkaar zetten van een meubelstuk vereist een basiskennis van hoeken.
• Navigatie: Of je nu een zeilboot bestuurt of een kaart leest tijdens het wandelen, hoeken spelen een cruciale rol bij het bepalen van je richting.
• Computergraphics: In de wereld van videogames en 3D-modellering is het manipuleren van objecten en het creëren van realistische beelden ondenkbaar zonder de kennis van hoeken.
• Het begrijpen van de wereld om ons heen: De zon die onder een bepaalde hoek op de aarde schijnt, de manier waarop een vogel vliegt, zelfs de manier waarop je een bal gooit - hoeken zijn overal.

Het begrijpen van hoeken stelt je in staat om de wereld om je heen beter te begrijpen en problemen creatiever op te lossen.

De Basisprincipes: Graden, Radialen en Hoektypes

Voordat we de diepte ingaan, moeten we eerst de basisprincipes vaststellen. Er zijn verschillende manieren om hoeken te meten, maar de meest voorkomende is in graden. Een volledige cirkel bevat 360 graden. Een rechte hoek is 90 graden, en een gestrekte hoek is 180 graden.

Een andere manier om hoeken te meten is in radialen. Eén radiaal is de hoek die wordt gevormd door een booglengte die gelijk is aan de straal van de cirkel. Een volledige cirkel is 2π radialen. De conversie tussen graden en radialen is als volgt:

• Graden = Radialen * (180/π)
• Radialen = Graden * (π/180)

Verschillende soorten hoeken zijn:

• Scherpe hoek: Minder dan 90 graden.
• Rechte hoek: Precies 90 graden.
• Stompe hoek: Tussen 90 en 180 graden.
• Gestrekte hoek: Precies 180 graden.
• Reflex hoek: Tussen 180 en 360 graden.
• Volle hoek: Precies 360 graden.

Methoden om Hoekgraden te Berekenen

Nu we de basis kennen, kunnen we kijken naar verschillende methoden om hoekgraden te berekenen.

1. Gebruik van een Gradenboog

De meest directe manier om een hoek te meten is met een gradenboog (ook wel geodriehoek genoemd). Dit instrument is speciaal ontworpen om hoeken te meten in graden. Plaats het middelpunt van de gradenboog op het hoekpunt van de hoek en lees de waarde af waar de lijnen van de hoek de schaal van de gradenboog kruisen.

Voordeel: Eenvoudig en snel. Nadeel: Minder nauwkeurig voor zeer kleine hoeken of hoeken die niet perfect op de gradenboog passen.

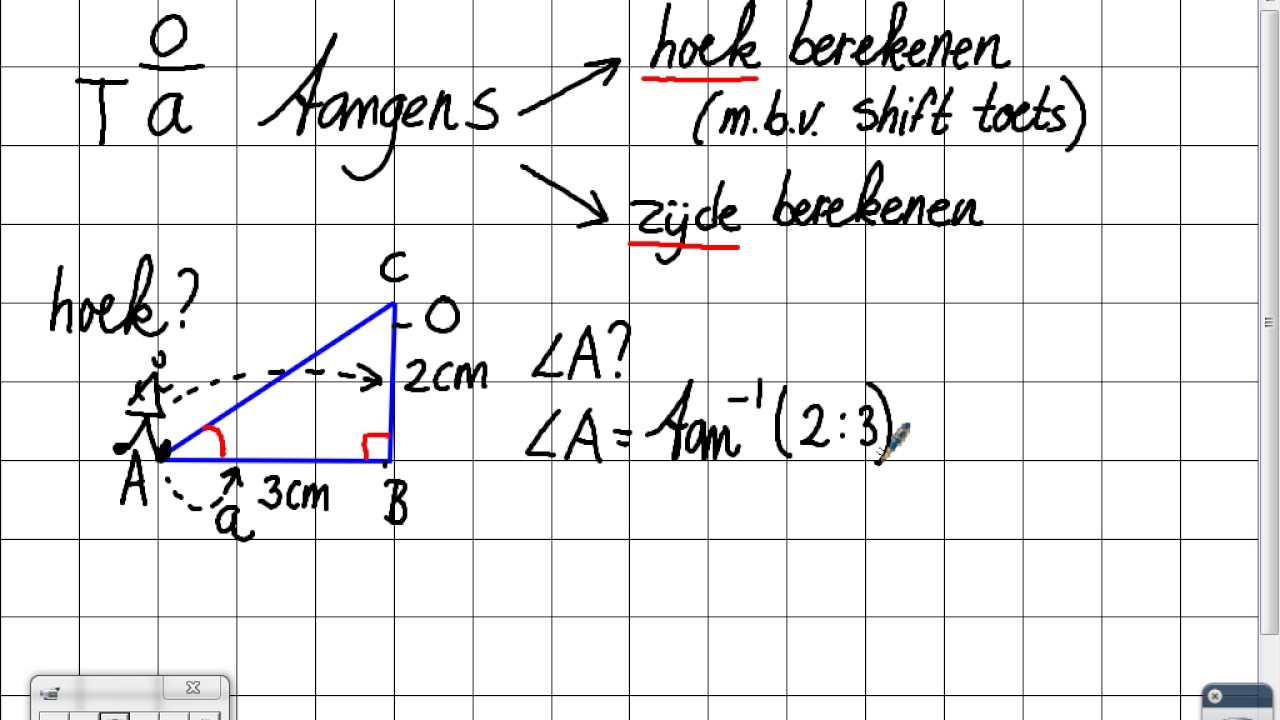
2. Gebruik van Trigonometrie

Trigonometrie is een tak van de wiskunde die zich bezighoudt met de relaties tussen de zijden en hoeken van driehoeken. De belangrijkste trigonometrische functies zijn sinus (sin), cosinus (cos) en tangens (tan). Deze functies kunnen worden gebruikt om de hoeken van een rechthoekige driehoek te berekenen als de lengtes van de zijden bekend zijn.

Stel je voor dat je een rechthoekige driehoek hebt. Dan geldt:

• sin(hoek) = Overstaande zijde / Schuine zijde
• cos(hoek) = Aanliggende zijde / Schuine zijde
• tan(hoek) = Overstaande zijde / Aanliggende zijde

Om de hoek te berekenen, moet je de inverse trigonometrische functies gebruiken: arcsinus (sin^-1), arccosinus (cos^-1) en arctangens (tan^-1). Deze functies vind je meestal op een wetenschappelijke rekenmachine of online calculator.

Voorbeeld: Stel dat de overstaande zijde van een hoek 3 cm is en de aanliggende zijde 4 cm. Dan is tan(hoek) = 3/4 = 0.75. Om de hoek te vinden, gebruik je arctan(0.75) ≈ 36.87 graden.

Voordeel: Zeer nauwkeurig, vooral als je de lengtes van de zijden precies weet. Nadeel: Vereist kennis van trigonometrie en een wetenschappelijke rekenmachine.

3. Gebruik van de Hoeksom in Driehoeken en Vierhoeken

Een belangrijke regel in de geometrie is dat de som van de hoeken in een driehoek altijd 180 graden is. In een vierhoek is de som van de hoeken altijd 360 graden. Als je de waarde van enkele hoeken weet, kun je de ontbrekende hoek berekenen door de bekende hoeken van het totaal af te trekken.

Voorbeeld: Stel dat je een driehoek hebt met hoeken van 60 en 80 graden. De derde hoek is dan 180 - 60 - 80 = 40 graden.

Voordeel: Eenvoudig en vereist geen speciale instrumenten. Nadeel: Alleen toepasbaar als je andere hoeken al kent.

4. Gebruik van Geometrische Relaties

Er zijn verschillende geometrische relaties die je kunt gebruiken om hoeken te berekenen. Bijvoorbeeld:

• Overstaande hoeken: Overstaande hoeken zijn gelijk aan elkaar.
• Aanliggende hoeken: Aanliggende hoeken vormen samen een rechte lijn (180 graden).
• Correspondentiehoeken: Correspondentiehoeken zijn gelijk aan elkaar als twee lijnen parallel zijn.
• Verwisselende binnenhoeken: Verwisselende binnenhoeken zijn gelijk aan elkaar als twee lijnen parallel zijn.

Door deze relaties te herkennen, kun je ontbrekende hoeken afleiden zonder directe meting.

Voordeel: Vereist geen metingen, alleen visuele herkenning van geometrische patronen. Nadeel: Vereist een goed begrip van geometrische principes.

Counterpoints: "Wanneer is Nauwkeurigheid Echt Nodig?"

Natuurlijk is niet elke situatie hetzelfde. Soms is een ruwe schatting voldoende, terwijl andere situaties extreme precisie vereisen. Bij het ophangen van een schilderij in je woonkamer is een paar graden verschil waarschijnlijk niet merkbaar. Maar bij de constructie van een brug of een vliegtuig, is een kleine afwijking fataal. Het is belangrijk om te bepalen hoe nauwkeurig je meting moet zijn en de juiste methode te kiezen.

Er zijn ook situaties waarin je misschien denkt dat je geen hoeken hoeft te berekenen, bijvoorbeeld als je een computerprogramma gebruikt. Maar zelfs dan is het nuttig om de basisprincipes te begrijpen, zodat je de resultaten van het programma kunt interpreteren en controleren. Een basisbegrip helpt je fouten te herkennen en te voorkomen.

Tips en Trucs voor Nauwkeurige Hoekberekeningen

• Gebruik het juiste gereedschap: Investeer in een goede gradenboog of digitale hoekmeter voor nauwkeurige metingen.
• Controleer je metingen: Meet de hoek meerdere keren en neem het gemiddelde om fouten te minimaliseren.
• Wees consistent met eenheden: Zorg ervoor dat je altijd in graden of radialen werkt en converteer tussen de eenheden indien nodig.
• Maak een schets: Een duidelijke schets van het probleem kan helpen om de relaties tussen de hoeken en zijden te visualiseren.
• Oefen, oefen, oefen: Net als bij elke vaardigheid, wordt je beter in het berekenen van hoeken door te oefenen.

Online Hulpmiddelen en Calculators

Gelukkig zijn er talloze online hulpmiddelen en calculators beschikbaar die je kunnen helpen bij het berekenen van hoeken. Deze tools kunnen bijzonder handig zijn voor complexe berekeningen of als je geen wetenschappelijke rekenmachine hebt.

Enkele populaire opties zijn:

• Online trigonometrie calculators
• Geometrie solvers
• Online gradenboog tools

Wees echter voorzichtig en controleer altijd de resultaten van deze tools, om zeker te zijn dat ze correct zijn.

Conclusie

Het berekenen van hoekgraden is een essentiële vaardigheid die in veel aspecten van ons leven van pas komt. Of je nu een klusproject uitvoert, een wiskundesom oplost, of gewoon de wereld om je heen beter wilt begrijpen, de kennis van hoeken is onmisbaar. We hebben verschillende methoden besproken, van het gebruik van een gradenboog tot trigonometrie, en we hebben benadrukt dat nauwkeurigheid belangrijk is, maar niet altijd nodig. Onthoud dat oefening kunst baart, dus blijf oefenen en experimenteren!

Nu je de basisprincipes en verschillende methoden kent, voel je je dan zelfverzekerd genoeg om een nieuwe uitdaging aan te gaan waarin hoekberekening belangrijk is? Welk project of probleem ga jij nu tackelen met je nieuwe kennis?