Hoe Bereken Je De Discriminant

Ben je ooit een wiskundige vergelijking tegengekomen die je deed duizelen? Een kwadratische vergelijking, om precies te zijn? Geen zorgen, je bent niet de enige! Veel mensen vinden het oplossen van kwadratische vergelijkingen uitdagend. Maar wat als ik je zou vertellen dat er een handige tool is die je kan helpen om snel inzicht te krijgen in de aard van de oplossingen, zonder dat je de hele vergelijking hoeft op te lossen? Die tool is de discriminant!

Dit artikel is speciaal geschreven voor leerlingen, studenten en iedereen die zijn wiskundige vaardigheden wil verbeteren. We zullen op een heldere en begrijpelijke manier uitleggen wat de discriminant is, hoe je deze berekent en hoe je de uitkomst interpreteert. Geen ingewikkelde formules of abstracte theorieën, maar een praktische gids om je te helpen kwadratische vergelijkingen te begrijpen als een pro!

Wat is de Discriminant?

De discriminant is een wiskundige term die je helpt te bepalen hoeveel en wat voor soort oplossingen een kwadratische vergelijking heeft. Het is als een soort "voorspeller" voor de oplossingen van de vergelijking.

Een kwadratische vergelijking heeft de algemene vorm:

ax² + bx + c = 0

waarbij:

• a, b en c coëfficiënten zijn (getallen).
• x de variabele is die we proberen op te lossen.
• a mag niet gelijk zijn aan 0, anders is het geen kwadratische vergelijking meer.

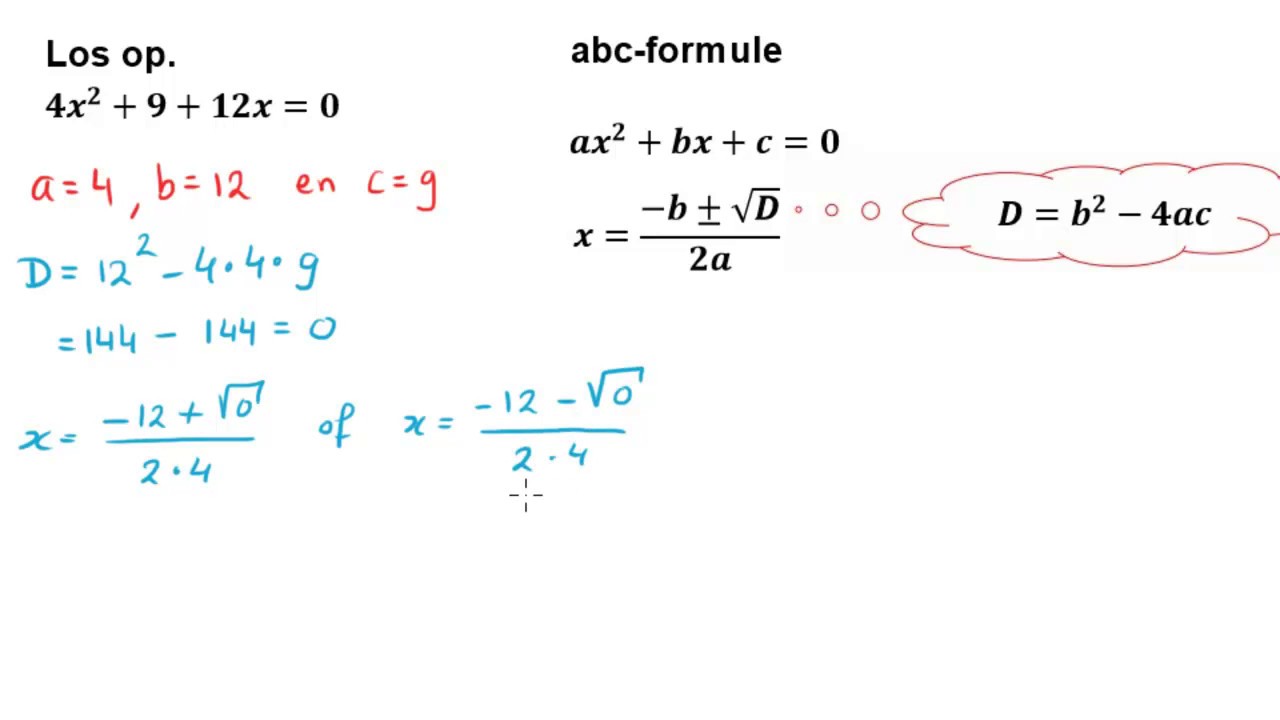
De discriminant, vaak aangeduid met de letter D (of soms met de Griekse letter Δ (delta)), wordt berekend met de volgende formule:

D = b² - 4ac

Kijk, dat valt best mee, toch? Het is gewoon een kwestie van de juiste waarden invullen in de formule. Laten we eens kijken hoe we dit in de praktijk kunnen brengen.

Hoe Bereken Je De Discriminant?

Het berekenen van de discriminant is een rechttoe rechtaan proces. Je hoeft alleen maar de waarden van de coëfficiënten a, b en c uit de kwadratische vergelijking te halen en deze in de formule D = b² - 4ac in te vullen. Hier zijn de stappen:

Stap 1: Identificeer a, b en c

De eerste stap is het identificeren van de waarden van a, b en c in je kwadratische vergelijking. Zorg ervoor dat je vergelijking in de standaardvorm ax² + bx + c = 0 staat. Laten we een paar voorbeelden bekijken:

• Voorbeeld 1: 2x² + 5x - 3 = 0
  • a = 2
  • b = 5
  • c = -3
• Voorbeeld 2: x² - 4x + 4 = 0
  • a = 1 (omdat x² hetzelfde is als 1x²)
  • b = -4
  • c = 4
• Voorbeeld 3: -3x² + 7x = 0
  • a = -3
  • b = 7
  • c = 0 (omdat er geen constante term is)

Stap 2: Vul de waarden in de formule in

Nu je de waarden van a, b en c hebt, kun je ze in de discriminantformule D = b² - 4ac invullen. Het is belangrijk om de tekens correct over te nemen. Laten we de voorbeelden van hierboven gebruiken:

• Voorbeeld 1: 2x² + 5x - 3 = 0
  • D = (5)² - 4 * 2 * (-3)
  • D = 25 + 24
  • D = 49
• Voorbeeld 2: x² - 4x + 4 = 0
  • D = (-4)² - 4 * 1 * 4
  • D = 16 - 16
  • D = 0
• Voorbeeld 3: -3x² + 7x = 0
  • D = (7)² - 4 * (-3) * 0
  • D = 49 - 0
  • D = 49

Stap 3: Vereenvoudig de uitdrukking

Na het invullen van de waarden, vereenvoudig je de uitdrukking om de waarde van de discriminant te vinden. Dit is gewoon een kwestie van de rekenkundige bewerkingen uitvoeren. We hebben dit al gedaan in de voorbeelden hierboven.

Wat Betekent De Waarde Van De Discriminant?

De waarde van de discriminant vertelt ons veel over de aard van de oplossingen van de kwadratische vergelijking. Er zijn drie mogelijke scenario's:

• D > 0 (Discriminant is positief): De kwadratische vergelijking heeft twee verschillende reële oplossingen. Dit betekent dat de grafiek van de kwadratische functie (een parabool) de x-as op twee verschillende punten snijdt.
• D = 0 (Discriminant is nul): De kwadratische vergelijking heeft één reële oplossing (of twee gelijke reële oplossingen). Dit betekent dat de grafiek van de kwadratische functie de x-as raakt op één punt. We zeggen ook wel dat de vergelijking een dubbele wortel heeft.
• D < 0 (Discriminant is negatief): De kwadratische vergelijking heeft geen reële oplossingen. De oplossingen zijn complex (met een imaginair deel). Dit betekent dat de grafiek van de kwadratische functie de x-as niet snijdt.

Laten we terugkijken naar onze eerdere voorbeelden om te zien hoe dit in de praktijk werkt:

• Voorbeeld 1: 2x² + 5x - 3 = 0, D = 49 (positief) - Twee verschillende reële oplossingen.
• Voorbeeld 2: x² - 4x + 4 = 0, D = 0 - Eén reële oplossing (dubbele wortel).
• Voorbeeld 3: -3x² + 7x = 0, D = 49 (positief) - Twee verschillende reële oplossingen.

Waarom is de Discriminant Nuttig?

De discriminant is een krachtig hulpmiddel om verschillende redenen:

• Snel Inzicht: Je kunt snel bepalen of een kwadratische vergelijking reële oplossingen heeft zonder de hele vergelijking op te lossen. Dit bespaart tijd en moeite.
• Probleemoplossing: Het helpt je te begrijpen welke aanpak je moet gebruiken om een kwadratische vergelijking op te lossen. Als de discriminant negatief is, weet je dat je geen reële oplossingen zult vinden met de standaard methoden.
• Grafische Interpretatie: De discriminant helpt je te visualiseren hoe de grafiek van de kwadratische functie eruit ziet. Je weet of de parabool de x-as snijdt, raakt of niet snijdt.
• Praktische Toepassingen: Kwadratische vergelijkingen en de discriminant worden in verschillende gebieden gebruikt, zoals natuurkunde (bijvoorbeeld bij het berekenen van de baan van een projectiel), engineering en economie.

Voorbeelden uit de Praktijk

Laten we een paar real-world voorbeelden bekijken waar de discriminant van pas kan komen:

• Voorbeeld 1: Een bal gooien

  Stel je voor dat je een bal omhoog gooit. De hoogte van de bal op een bepaald moment kan worden beschreven door een kwadratische vergelijking. Met de discriminant kun je bepalen of de bal een bepaalde hoogte zal bereiken. Als de discriminant negatief is voor die hoogte, betekent dit dat de bal die hoogte nooit zal bereiken.

• Voorbeeld 2: Winstmaximalisatie

  Een bedrijf kan een kwadratische functie gebruiken om de winst te modelleren als functie van de verkoopprijs. De discriminant kan helpen bepalen of er een verkoopprijs is die winstgevend is (winst groter dan nul). Een negatieve discriminant zou betekenen dat het bedrijf geen winst kan maken, ongeacht de prijs.

Tips en Trucs

Hier zijn een paar tips en trucs om de discriminant nog gemakkelijker te gebruiken:

• Controleer de Tekens: Let goed op de tekens van de coëfficiënten a, b en c. Een verkeerd teken kan leiden tot een verkeerde berekening van de discriminant.
• Vereenvoudig Eerst: Als de kwadratische vergelijking niet in de standaardvorm staat, vereenvoudig deze dan eerst voordat je de waarden van a, b en c identificeert.
• Oefening Baart Kunst: Oefen met verschillende kwadratische vergelijkingen om vertrouwd te raken met het berekenen en interpreteren van de discriminant.
• Gebruik een Rekenmachine: Gebruik een rekenmachine om de berekeningen te versnellen en fouten te voorkomen, vooral bij grotere getallen.

Conclusie

De discriminant is een essentieel hulpmiddel voor iedereen die met kwadratische vergelijkingen werkt. Het stelt je in staat om snel en efficiënt inzicht te krijgen in de aard van de oplossingen, zonder de hele vergelijking op te lossen. Door de discriminant te berekenen en te interpreteren, kun je je wiskundige vaardigheden verbeteren en complexe problemen met vertrouwen aanpakken.

Onthoud dat wiskunde geen mysterie is, maar een reeks tools en technieken die je kunt leren beheersen. De discriminant is slechts één van die tools, maar het is een krachtige tool die je kan helpen om de wereld om je heen beter te begrijpen. Dus, ga ermee aan de slag, oefen, en ontdek de fascinerende wereld van kwadratische vergelijkingen!

Hopelijk heeft dit artikel je geholpen om de discriminant beter te begrijpen. Blijf leren, blijf oefenen, en wie weet, misschien word jij wel de volgende wiskundige held!