Hoe Bereken Je De Inhoud Van Een Prisma

Heb je ooit naar een Toblerone-reep gekeken en je afgevraagd hoeveel chocolade er precies in zit? Of misschien ben je wel bezig met een knutselproject en wil je weten hoeveel verf je nodig hebt om een prisma te beschilderen? Het berekenen van de inhoud van een prisma lijkt misschien ingewikkeld, maar geloof me, het is makkelijker dan je denkt! Veel mensen worstelen met ruimtelijke figuren, vooral als het gaat om het onthouden van formules en het correct toepassen ervan. Maar geen zorgen, in dit artikel gaan we je stap voor stap uitleggen hoe je de inhoud van een prisma kunt berekenen, zodat je nooit meer voor verrassingen komt te staan.

Wat is een Prisma eigenlijk?

Laten we beginnen met de basis. Een prisma is een driedimensionale figuur met twee identieke en parallelle vlakken, de zogenaamde grondvlakken. Deze grondvlakken kunnen elke veelhoek zijn: een driehoek, een vierkant, een zeshoek, enzovoort. De overige vlakken van een prisma zijn altijd rechthoeken (of parallellogrammen als het prisma scheef staat). Denk aan een tent (driehoekig prisma) of een doos tissues (rechthoekig prisma).

Belangrijk om te onthouden: Het woord 'prisma' zegt iets over de vorm, maar niet over de grootte. Er zijn kleine prisma's, grote prisma's, en alles daartussenin.

De Formule voor de Inhoud van een Prisma

De sleutel tot het berekenen van de inhoud van een prisma is de volgende formule:

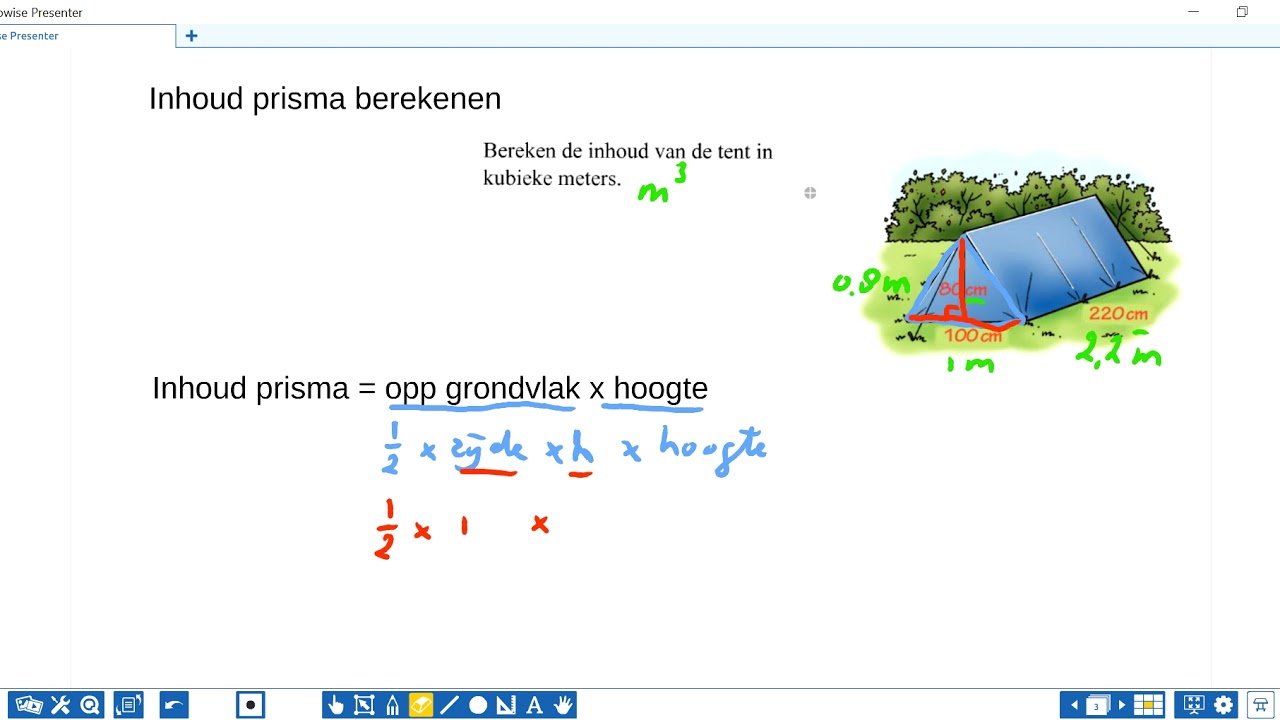
Inhoud = Oppervlakte van het grondvlak × Hoogte van het prisma

Laten we deze formule eens ontleden:

Oppervlakte van het grondvlak (G): Dit is de oppervlakte van de vorm die het grondvlak van het prisma vormt. Afhankelijk van de vorm (driehoek, vierkant, enz.) gebruik je de juiste formule om de oppervlakte te berekenen.
Hoogte van het prisma (h): Dit is de loodrechte afstand tussen de twee grondvlakken. Het is niet noodzakelijkerwijs de langste zijde van het prisma.

Dus, als je de oppervlakte van het grondvlak en de hoogte van het prisma weet, kun je de inhoud eenvoudigweg berekenen door ze met elkaar te vermenigvuldigen.

Stap-voor-stap: Hoe Bereken Je de Inhoud van een Prisma?

Hier is een stapsgewijze handleiding voor het berekenen van de inhoud van een prisma:

Stap 1: Identificeer de vorm van het grondvlak

Kijk naar de twee identieke en parallelle vlakken van het prisma. Is het een driehoek, een vierkant, een rechthoek, een vijfhoek, of iets anders? Dit is cruciaal omdat de vorm van het grondvlak bepaalt welke formule je nodig hebt om de oppervlakte te berekenen.

Stap 2: Bereken de oppervlakte van het grondvlak

Nu komt de geometrie van de vlakke figuren om de hoek kijken. Hier zijn enkele veelvoorkomende formules die je kunt gebruiken:

Driehoek: G = (1/2) × basis × hoogte (van de driehoek!)
Vierkant: G = zijde × zijde
Rechthoek: G = lengte × breedte
Cirkel: G = π × straal² (Dit zou een cilinder zijn, maar het principe blijft hetzelfde!)
Regelmatige veelhoek: G = (1/2) × omtrek × apothem (De "apothem" is de afstand van het middelpunt van de veelhoek tot het midden van een zijde.)

Tip: Als je de oppervlakte van een complexere vorm niet direct kunt berekenen, probeer deze dan op te delen in eenvoudigere vormen (zoals driehoeken en rechthoeken) waarvan je wel de oppervlakte kunt berekenen.

Stap 3: Bepaal de hoogte van het prisma

De hoogte van het prisma is de loodrechte afstand tussen de twee grondvlakken. Zorg ervoor dat je de hoogte loodrecht meet, dus in een rechte hoek met de grondvlakken. Als het prisma op zijn 'kant' ligt, kan het even duren voordat je de juiste hoogte hebt gevonden.

Stap 4: Vermenigvuldig de oppervlakte van het grondvlak met de hoogte

Nu komt het makkelijke deel. Vermenigvuldig de oppervlakte van het grondvlak (die je in stap 2 hebt berekend) met de hoogte van het prisma (die je in stap 3 hebt bepaald). Het resultaat is de inhoud van het prisma!

Inhoud = G × h

Stap 5: Vergeet de eenheden niet!

De inhoud wordt altijd uitgedrukt in kubieke eenheden. Dus, als de afmetingen van het prisma in centimeters zijn, dan is de inhoud in kubieke centimeters (cm³). Als de afmetingen in meters zijn, dan is de inhoud in kubieke meters (m³), enzovoort.

Voorbeelden om het te Laten Zien

Laten we een paar voorbeelden bekijken om het allemaal wat duidelijker te maken:

Voorbeeld 1: Driehoekig Prisma

Stel, we hebben een driehoekig prisma. De basis van de driehoek is 6 cm, de hoogte van de driehoek is 4 cm, en de hoogte van het prisma is 10 cm. Wat is de inhoud van het prisma?

Vorm van het grondvlak: Driehoek
Oppervlakte van het grondvlak: G = (1/2) × 6 cm × 4 cm = 12 cm²
Hoogte van het prisma: h = 10 cm
Inhoud: Inhoud = 12 cm² × 10 cm = 120 cm³

Dus, de inhoud van het driehoekige prisma is 120 kubieke centimeters.

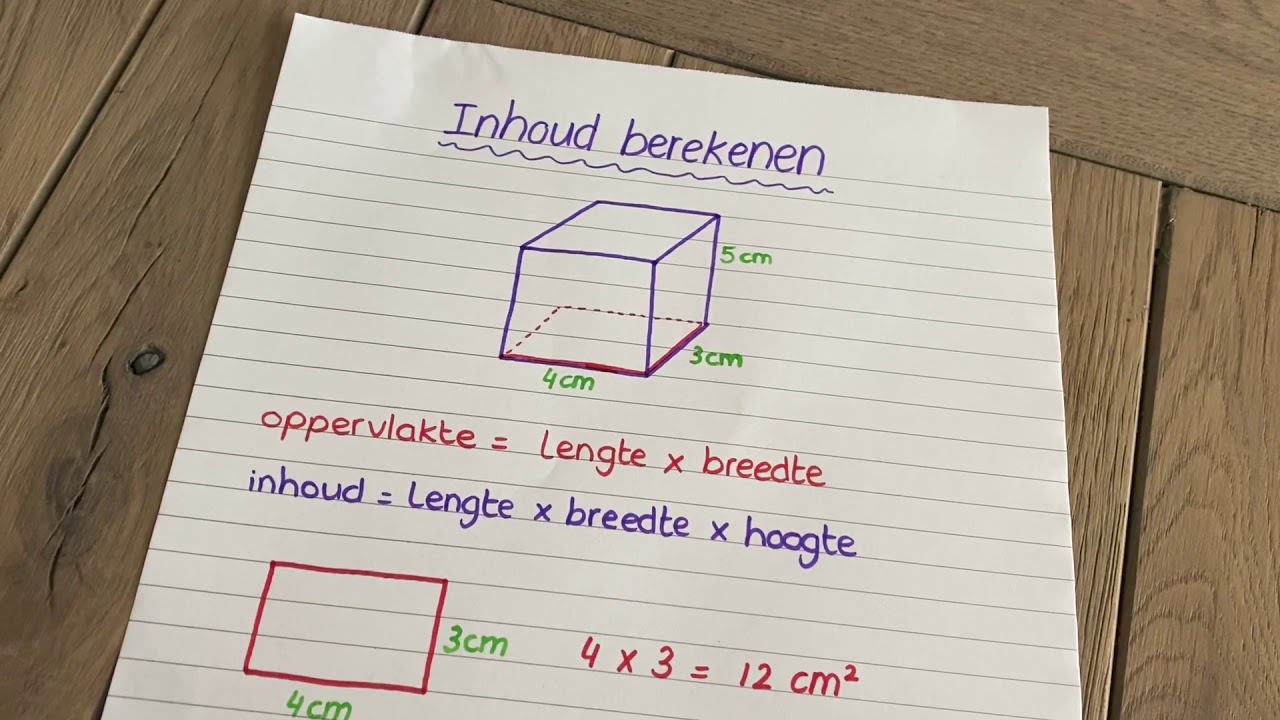
Voorbeeld 2: Rechthoekig Prisma

Stel, we hebben een rechthoekig prisma (een blok). De lengte van het grondvlak is 8 cm, de breedte is 5 cm, en de hoogte van het prisma is 7 cm. Wat is de inhoud van het prisma?

Vorm van het grondvlak: Rechthoek
Oppervlakte van het grondvlak: G = 8 cm × 5 cm = 40 cm²
Hoogte van het prisma: h = 7 cm
Inhoud: Inhoud = 40 cm² × 7 cm = 280 cm³

Dus, de inhoud van het rechthoekige prisma is 280 kubieke centimeters.

Veelvoorkomende Fouten om te Vermijden

Hier zijn enkele veelvoorkomende fouten die mensen maken bij het berekenen van de inhoud van een prisma:

De verkeerde hoogte gebruiken: Zorg ervoor dat je de loodrechte afstand tussen de grondvlakken gebruikt.
De oppervlakteformule voor het grondvlak vergeten: Ken je formules voor de oppervlakte van verschillende vlakke figuren.
De eenheden vergeten: Vergeet niet de eenheden op te schrijven en zorg ervoor dat de inhoud in kubieke eenheden wordt uitgedrukt.
Verwarring tussen oppervlakte en inhoud: Oppervlakte is de totale oppervlakte van alle vlakken, terwijl inhoud de ruimte is die het prisma inneemt.

Waarom is dit Belangrijk?

Het berekenen van de inhoud van een prisma is niet alleen een abstracte wiskundeoefening. Het heeft tal van praktische toepassingen in het dagelijks leven en in verschillende vakgebieden, zoals:

Bouwkunde: Het berekenen van de hoeveelheid beton die nodig is voor een pilaar.
Verpakking: Het bepalen van de grootte van een doos om een bepaald product in te passen.
Engineering: Het ontwerpen van bruggen en andere structuren.
Wiskunde en Natuurkunde: Het berekenen van volume bij verschillende vraagstukken.
Hobby en Knutselen: Het inschatten van de hoeveelheid materiaal die je nodig hebt voor een project.

Kortom, het begrijpen van hoe je de inhoud van een prisma berekent, kan je helpen bij het oplossen van allerlei problemen, zowel in de schoolbanken als daarbuiten.

Conclusie

Het berekenen van de inhoud van een prisma is een essentiële vaardigheid die je in veel situaties van pas kan komen. Met de formule (Inhoud = Oppervlakte van het grondvlak × Hoogte) en de stapsgewijze handleiding die we in dit artikel hebben besproken, ben je nu in staat om de inhoud van elk prisma te berekenen, ongeacht de vorm van het grondvlak. Dus, pak een pen en papier, en begin met oefenen. Voor je het weet, ben je een ware prisma-inhoud-expert!