Hoe Bereken Je De N Term

Ken je dat gevoel? Je zit midden in een wiskundeopgave, staart naar een reeks getallen, en je vraagt je af: waar komt dit vandaan? Hoe kan ik het volgende getal in deze reeks voorspellen? Of misschien nog wel belangrijker: hoe bereken ik de n-de term?

Als wiskunde je nachtmerrie is, geen zorgen! Je bent niet de enige. Veel mensen vinden het lastig om patronen in getallen te herkennen en om formules te ontwikkelen die deze patronen beschrijven. Maar geloof me, het is absoluut te leren. En dat is precies waar we het vandaag over gaan hebben: het berekenen van de n-de term.

We gaan stap voor stap door de verschillende methoden en technieken die je kunt gebruiken. Geen ingewikkelde wiskundige jargon, maar duidelijke uitleg en praktische voorbeelden. Dus pak pen en papier, en laten we aan de slag gaan!

Wat is de N-de Term Eigenlijk?

Voordat we in de details duiken, is het belangrijk om te begrijpen wat de n-de term precies is. In essentie is de n-de term een algemene formule die je kunt gebruiken om elk getal in een reeks te bepalen. De 'n' staat voor de positie van het getal in de reeks. Dus, als je de 10e term wilt weten, vervang je 'n' door 10 in de formule.

Stel je voor, je hebt een reeks: 2, 4, 6, 8, 10... Intuïtief zie je waarschijnlijk al dat dit de reeks van even getallen is. De n-de term voor deze reeks zou zijn: 2n. Als je de 5e term wilt weten, vervang je n door 5: 2 * 5 = 10. En inderdaad, de 5e term is 10!

Dit is een simpel voorbeeld, maar het laat zien hoe krachtig de n-de term kan zijn. Het stelt je in staat om willekeurige termen in een reeks te bepalen, zonder dat je alle voorgaande termen hoeft uit te rekenen.

Verschillende Soorten Rijen en Hun N-de Term

Er zijn verschillende soorten rijen, elk met hun eigen manier om de n-de term te berekenen. Laten we een paar veelvoorkomende typen bekijken:

1. Aritmetische Rijen

Een aritmetische rij is een reeks getallen waarbij het verschil tussen opeenvolgende termen constant is. Dit constante verschil noemen we de gemeenschappelijke differentie (d).

Bijvoorbeeld: 3, 7, 11, 15, 19... Hier is de gemeenschappelijke differentie 4 (7-3 = 4, 11-7 = 4, enz.).

De formule voor de n-de term van een aritmetische rij is:

a_n = a₁ + (n - 1) * d

Waarbij:

a_n de n-de term is
a₁ de eerste term is
n de positie van de term in de reeks is
d de gemeenschappelijke differentie is

Laten we dit toepassen op de bovenstaande reeks: 3, 7, 11, 15, 19...

a₁ = 3
d = 4

Dus, de n-de term is: a_n = 3 + (n - 1) * 4 = 3 + 4n - 4 = 4n - 1

Als we de 10e term willen weten: a₁₀ = 4 * 10 - 1 = 39

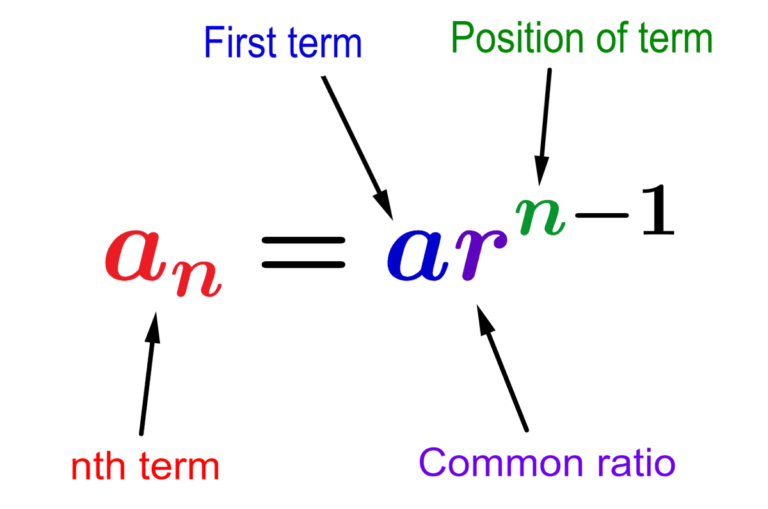
2. Meetkundige Rijen

Een meetkundige rij is een reeks getallen waarbij elke term wordt verkregen door de vorige term te vermenigvuldigen met een constante factor. Deze constante factor noemen we de gemeenschappelijke ratio (r).

Bijvoorbeeld: 2, 6, 18, 54, 162... Hier is de gemeenschappelijke ratio 3 (6/2 = 3, 18/6 = 3, enz.).

De formule voor de n-de term van een meetkundige rij is:

a_n = a₁ * r^{(n - 1)}

Waarbij:

a_n de n-de term is
a₁ de eerste term is
n de positie van de term in de reeks is
r de gemeenschappelijke ratio is

Laten we dit toepassen op de bovenstaande reeks: 2, 6, 18, 54, 162...

a₁ = 2
r = 3

Dus, de n-de term is: a_n = 2 * 3^{(n - 1)}

Als we de 5e term willen weten: a₅ = 2 * 3^{(5 - 1)} = 2 * 3⁴ = 2 * 81 = 162

3. Kwadratische Rijen

Een kwadratische rij is een reeks waarbij het verschil tussen de opeenvolgende termen niet constant is, maar het verschil van de verschillen wel constant is. Dit impliceert dat de n-de term een kwadratische expressie zal zijn.

Bijvoorbeeld: 2, 5, 10, 17, 26... De verschillen zijn: 3, 5, 7, 9... en de verschillen van de verschillen zijn: 2, 2, 2... (constant).

De n-de term voor een kwadratische rij heeft de vorm: a_n = an² + bn + c

Om de waarden van a, b en c te vinden, heb je minimaal 3 termen van de rij nodig. Er zijn verschillende methoden om dit te doen, waaronder het oplossen van een stelsel van vergelijkingen. Dit kan wat complexer zijn, maar er zijn online tools en rekenmachines die je hierbij kunnen helpen.

Praktische Tips voor het Berekenen van de N-de Term

Oké, we hebben nu de basisprincipes behandeld. Hier zijn een paar praktische tips die je kunt gebruiken bij het berekenen van de n-de term:

Analyseer de reeks: Kijk goed naar de reeks en probeer patronen te herkennen. Is er een constant verschil? Een constante ratio? Zijn de verschillen aan het toenemen of afnemen?
Bereken de verschillen (en de verschillen van de verschillen): Dit helpt je om te bepalen of de rij aritmetisch, meetkundig of kwadratisch is.
Gebruik de juiste formule: Zodra je het type rij hebt geïdentificeerd, gebruik je de corresponderende formule voor de n-de term.
Test je formule: Vervang n door een paar bekende waarden om te controleren of de formule correct is.
Wees niet bang om te experimenteren: Soms is er geen "rechte" formule. Probeer verschillende benaderingen en kijk wat werkt.
Gebruik online tools: Er zijn talloze online rekenmachines en solvers die je kunnen helpen bij het berekenen van de n-de term. Zoek bijvoorbeeld naar "sequence calculator" of "nth term calculator".

Voorbeelden Uit Het Dagelijks Leven

Je denkt misschien: "Wanneer ga ik dit in de praktijk gebruiken?" Nou, verrassend genoeg komt het berekenen van de n-de term vaker voor dan je denkt! Hier zijn een paar voorbeelden:

Rente berekenen: Bij het berekenen van samengestelde rente kan de formule voor een meetkundige rij worden gebruikt om het saldo na een bepaald aantal periodes te bepalen.
Voorspellen van verkopen: Bedrijven kunnen rijen gebruiken om trends in verkopen te analyseren en toekomstige verkopen te voorspellen.
Patronen in de natuur: Veel patronen in de natuur, zoals de Fibonacci-reeks (die verband houdt met de gulden snede), kunnen worden beschreven met behulp van wiskundige rijen.
Programmeren: In de informatica worden rijen en reeksen vaak gebruikt om algoritmen te ontwikkelen en data te analyseren.

Conclusie

Het berekenen van de n-de term kan in het begin misschien intimiderend lijken, maar met de juiste kennis en oefening kan het een waardevolle vaardigheid zijn. Door de verschillende soorten rijen te begrijpen en de bijbehorende formules te kennen, kun je patronen herkennen en toekomstige waarden voorspellen. Vergeet niet om de tips te volgen, te experimenteren en gebruik te maken van online tools als je vastloopt.

Dus, de volgende keer dat je een reeks getallen tegenkomt, ga de uitdaging aan en probeer de n-de term te berekenen. Je zult versteld staan van wat je kunt bereiken!

En onthoud, wiskunde is niet eng. Het is een krachtig hulpmiddel dat ons helpt om de wereld om ons heen beter te begrijpen. Veel succes!