Hoe Bereken Je De Schuine Zijde Van Een Driehoek

Heb je je ooit afgevraagd hoe je de lengte van de schuine zijde van een driehoek kunt berekenen? Misschien sta je voor een klus in huis, zoals het bouwen van een schuur, of heb je een wiskundeprobleem dat je maar niet opgelost krijgt. Wat de reden ook is, het berekenen van de schuine zijde is een essentiële vaardigheid, en gelukkig is het helemaal niet zo ingewikkeld als het lijkt!

Veel mensen worstelen met geometrie, vooral als het gaat om het toepassen van theorieën in de praktijk. De Pythagoras stelling, de sleutel tot het berekenen van de schuine zijde, klinkt misschien intimiderend, maar met een beetje uitleg en oefening, wordt het een tweede natuur.

Wat is de Schuine Zijde Eigenlijk?

Voordat we in de berekening duiken, is het belangrijk om te begrijpen wat de schuine zijde precies is. De schuine zijde is de langste zijde van een rechthoekige driehoek. Een rechthoekige driehoek is een driehoek met één hoek van precies 90 graden (een rechte hoek).

De schuine zijde bevindt zich altijd tegenover de rechte hoek. De andere twee zijden van de rechthoekige driehoek, die de rechte hoek vormen, worden de rechthoekszijden genoemd.

Samenvattend:

• Schuine zijde: De langste zijde, tegenover de rechte hoek.
• Rechthoekszijden: De twee kortere zijden die de rechte hoek vormen.

De Pythagoras Stelling: A² + B² = C²

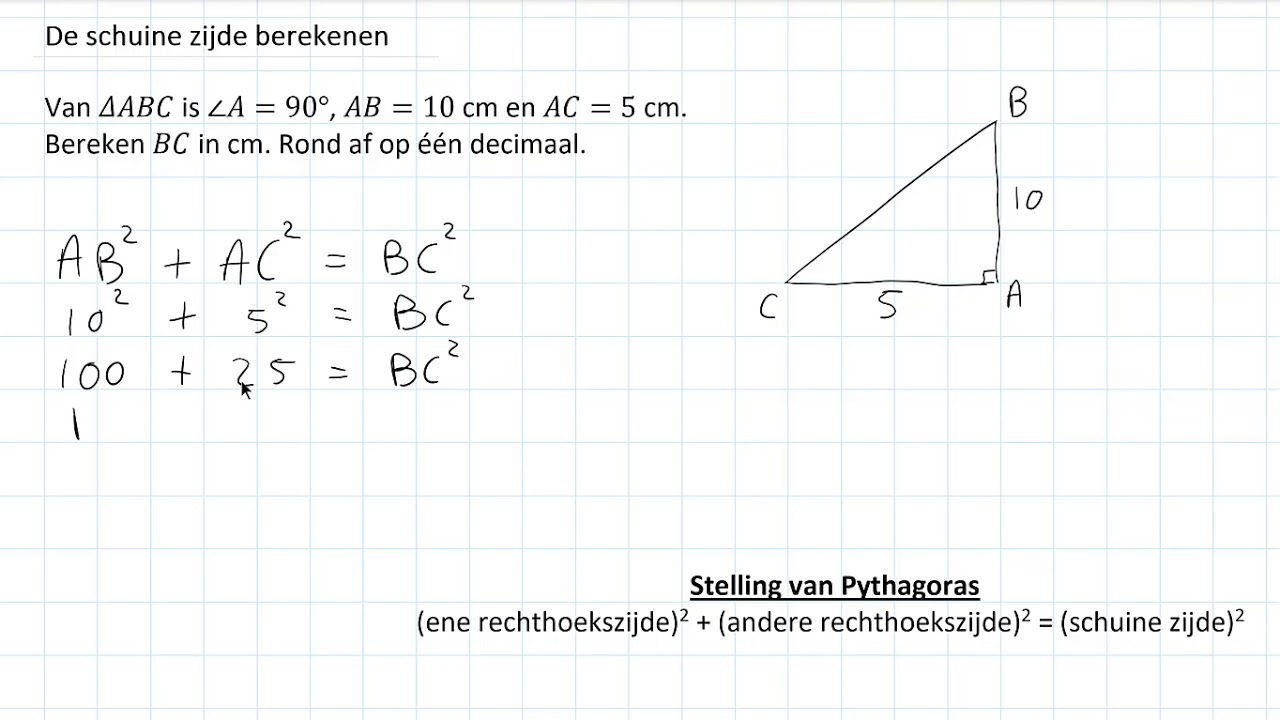
De Pythagoras stelling is de fundamentele formule voor het berekenen van de schuine zijde van een rechthoekige driehoek. De stelling zegt dat in een rechthoekige driehoek het kwadraat van de lengte van de schuine zijde (c) gelijk is aan de som van de kwadraten van de lengtes van de rechthoekszijden (a en b).

In formulevorm: a² + b² = c²

Wat betekent dit?

Stel je voor dat je een rechthoekige driehoek hebt waarbij de ene rechthoekszijde (a) 3 cm lang is en de andere rechthoekszijde (b) 4 cm lang is. Om de lengte van de schuine zijde (c) te vinden, volg je deze stappen:

1. Kwadrateer de lengtes van de rechthoekszijden:
   • a² = 3² = 9
   • b² = 4² = 16
2. Tel de kwadraten bij elkaar op:
   • a² + b² = 9 + 16 = 25
3. Neem de vierkantswortel van de som:
   • c = √25 = 5

Dus, de lengte van de schuine zijde is 5 cm.

Een Stap-voor-Stap Handleiding met Voorbeelden

Stap 1: Identificeer de Rechthoekszijden (a en b)

Zorg ervoor dat je weet welke zijden de rechthoekszijden zijn. Ze vormen de rechte hoek. Het maakt niet uit welke je a en welke je b noemt.

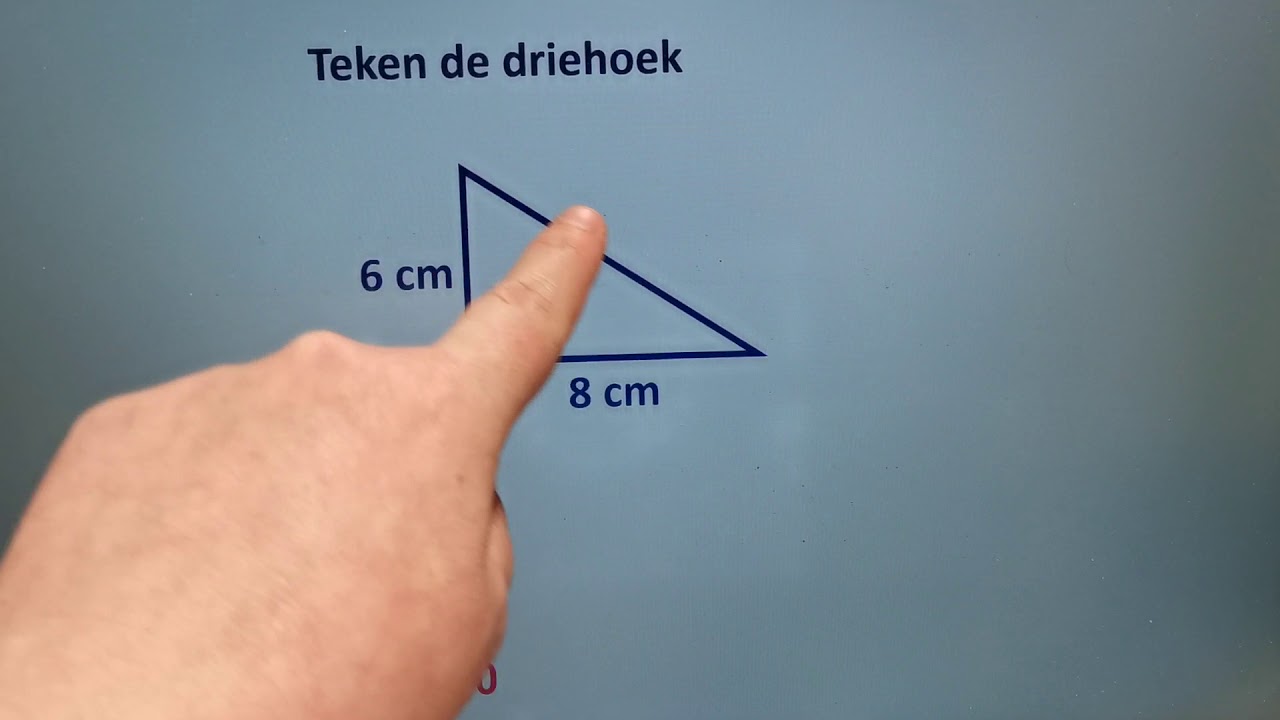
Voorbeeld 1: Een rechthoekige driehoek heeft rechthoekszijden van 6 meter en 8 meter. We kunnen zeggen: a = 6 meter en b = 8 meter.

Stap 2: Kwadrateer de Lengtes van de Rechthoekszijden

Vermenigvuldig de lengte van elke rechthoekszijde met zichzelf.

Voorbeeld 1 (vervolg):

• a² = 6² = 36
• b² = 8² = 64

Stap 3: Tel de Kwadraten bij Elkaar Op

Addeer de resultaten van de kwadraten van de rechthoekszijden.

Voorbeeld 1 (vervolg):

• a² + b² = 36 + 64 = 100

Stap 4: Neem de Vierkantswortel van de Som

Zoek de vierkantswortel van de som. Dit is de lengte van de schuine zijde (c).

Voorbeeld 1 (vervolg):

• c = √100 = 10

Dus, de lengte van de schuine zijde is 10 meter.

Nog een Voorbeeld:

Stel, a = 5 cm en b = 12 cm.

1. a² = 5² = 25
2. b² = 12² = 144
3. a² + b² = 25 + 144 = 169
4. c = √169 = 13

De schuine zijde (c) is 13 cm.

Wanneer Heb Je Dit Nodig? Praktische Toepassingen

De Pythagoras stelling is niet alleen nuttig voor wiskunde examens. Het heeft tal van praktische toepassingen in het dagelijks leven:

• Constructie: Om de lengte van een dakspant te bepalen of de diagonaal van een rechthoekige fundering te berekenen.
• Navigatie: Om de kortste afstand tussen twee punten te bepalen, bijvoorbeeld bij het zeilen of vliegen.
• Engineering: Bij het ontwerpen van bruggen, gebouwen en andere structuren.
• Doe-het-zelf projecten: Bij het bouwen van een schutting, een trap of een schuur.

Stel je voor dat je een ladder tegen een muur plaatst. Je weet de hoogte van de muur (a) en de afstand van de voet van de ladder tot de muur (b). Met de Pythagoras stelling kun je bepalen hoe lang de ladder (c) moet zijn om veilig de top van de muur te bereiken.

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Zelfs met een duidelijke formule, kunnen er fouten insluipen. Hier zijn enkele veelvoorkomende fouten en tips om ze te vermijden:

• Vergeten te kwadrateren: Zorg ervoor dat je *altijd* de lengtes van de rechthoekszijden kwadrateert voordat je ze optelt.
• Vergeten de vierkantswortel te trekken: Nadat je de kwadraten hebt opgeteld, moet je nog de vierkantswortel trekken om de uiteindelijke lengte van de schuine zijde te vinden.
• Verkeerde zijden identificeren: Zorg ervoor dat je de rechthoekszijden (a en b) correct identificeert en verwar ze niet met de schuine zijde (c).
• Werken met niet-rechthoekige driehoeken: De Pythagoras stelling geldt *alleen* voor rechthoekige driehoeken. Voor andere typen driehoeken heb je andere methoden nodig, zoals de sinus- en cosinusregels.

Tip: Controleer altijd je antwoord. De schuine zijde moet altijd de langste zijde van de driehoek zijn. Als je antwoord lager is dan een van de rechthoekszijden, heb je waarschijnlijk een fout gemaakt.

Online Hulpmiddelen en Rekenmachines

Er zijn tal van online calculators beschikbaar die de schuine zijde voor je kunnen berekenen. Zoek simpelweg op "Pythagoras calculator" of "schuine zijde berekenen" in je favoriete zoekmachine. Deze hulpmiddelen zijn handig om je antwoorden te controleren of om snel een berekening uit te voeren.

Let op: Hoewel deze calculators handig zijn, is het belangrijk om de principes achter de berekening te begrijpen. Zo kun je de stelling ook toepassen in situaties waar je geen toegang hebt tot een calculator.

Conclusie

Het berekenen van de schuine zijde van een rechthoekige driehoek is een vaardigheid die zowel nuttig als verrassend eenvoudig is. Met de Pythagoras stelling (a² + b² = c²) en een beetje oefening, kun je deze berekening met vertrouwen uitvoeren. Of je nu een wiskundeprobleem oplost, een constructieproject plant of gewoon je geometrische kennis wilt verbeteren, het beheersen van deze vaardigheid zal je zeker van pas komen.

Dus, de volgende keer dat je geconfronteerd wordt met een rechthoekige driehoek, onthoud dan de Pythagoras stelling, volg de stappen, en bereken die schuine zijde als een professional!