Hoe Bereken Je Een Breuk
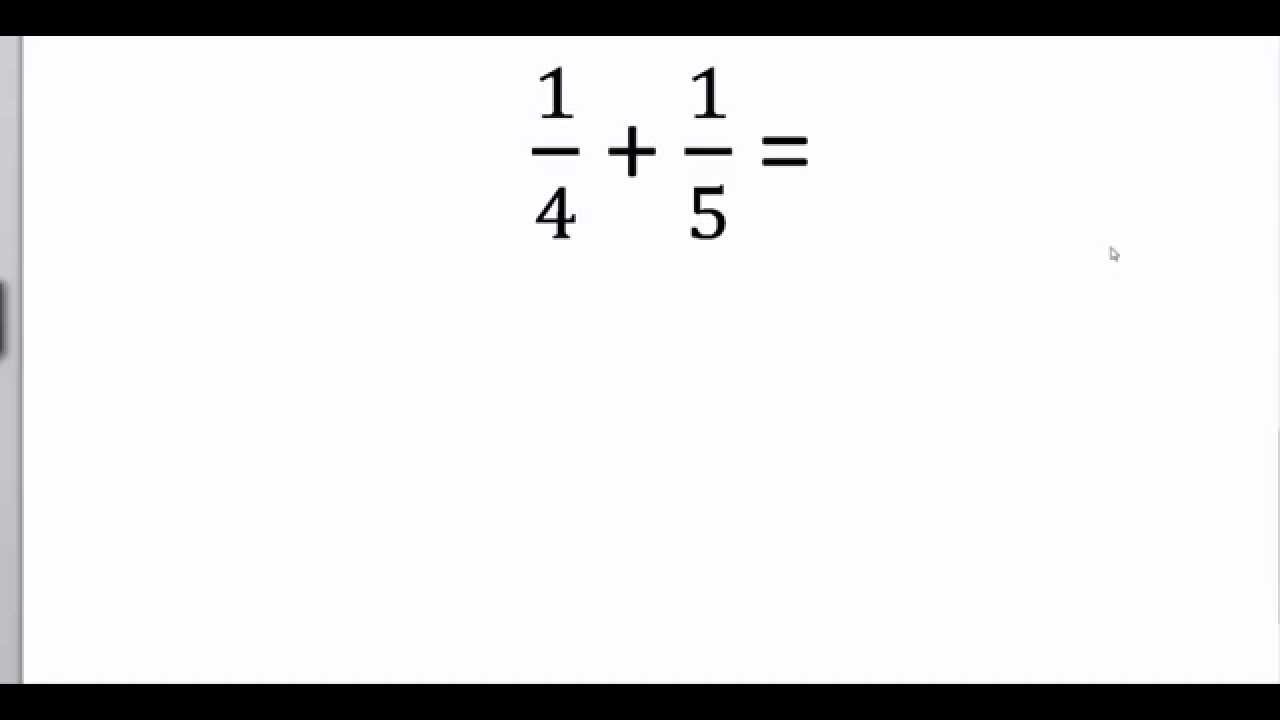
Heb je ooit naar een recept gekeken en gestruikeld over de hoeveelheid 1/3 kopje bloem? Of misschien probeerde je een pizza te verdelen en je af te vragen hoeveel stukken je eigenlijk overhoudt als je de helft van de helft opeet? Breuken kunnen soms ingewikkeld lijken, maar ze zijn eigenlijk heel alledaags en nuttig! Dit artikel is speciaal geschreven voor iedereen die de basisprincipes van breuken beter wil begrijpen, van studenten in de basisschool tot volwassenen die hun wiskundekennis willen opfrissen.
Wat is een breuk eigenlijk?
Een breuk is simpelweg een manier om een deel van een geheel te representeren. Stel je een pizza voor. Als je de pizza in vier gelijke stukken verdeelt, is elk stuk 1/4 (één vierde) van de pizza. De breuk 1/4 bestaat uit twee delen:
- De teller (1): Dit is het aantal delen dat je hebt.
- De noemer (4): Dit is het totale aantal delen waarin het geheel is verdeeld.
De streep tussen de teller en de noemer noemen we de breukstreep. Die staat eigenlijk voor delen door.
Verschillende soorten breuken
Er zijn verschillende soorten breuken die je moet kennen:
- Echte breuken: De teller is kleiner dan de noemer (bijvoorbeeld 1/2, 3/4, 5/8). Deze breuken vertegenwoordigen een waarde kleiner dan 1.
- Onechte breuken: De teller is groter dan of gelijk aan de noemer (bijvoorbeeld 5/4, 7/3, 8/8). Deze breuken vertegenwoordigen een waarde groter dan of gelijk aan 1.
- Gemengde getallen: Een combinatie van een heel getal en een echte breuk (bijvoorbeeld 1 1/2, 2 3/4, 5 1/3).
Het is belangrijk om het verschil tussen deze soorten te herkennen, omdat dit van invloed is op hoe je ermee rekent.
Hoe reken je met breuken?
Nu komen we bij het leuke gedeelte: hoe je daadwerkelijk met breuken rekent. We gaan de belangrijkste bewerkingen bekijken:
Breuken gelijknamig maken
Voordat je breuken kunt optellen of aftrekken, moeten ze gelijknamig zijn. Dit betekent dat ze dezelfde noemer moeten hebben. Stel je voor dat je 1/2 pizza wilt optellen bij 1/4 pizza. Je kunt deze niet direct optellen omdat de stukken niet even groot zijn.
Om breuken gelijknamig te maken, zoek je naar het kleinste gemene veelvoud (KGV) van de noemers. Dit is het kleinste getal dat deelbaar is door beide noemers.
Voorbeeld:
Maak 1/2 en 1/4 gelijknamig.
- De noemers zijn 2 en 4.
- Het KGV van 2 en 4 is 4.
- We moeten 1/2 omzetten naar een breuk met noemer 4.
- Om dit te doen, vermenigvuldigen we de teller en de noemer van 1/2 met 2: (1 * 2) / (2 * 2) = 2/4
- Nu hebben we 2/4 en 1/4, die gelijknamig zijn!
Breuken optellen en aftrekken
Zodra breuken gelijknamig zijn, is het optellen en aftrekken eenvoudig. Je telt of trekt alleen de tellers op/af. De noemer blijft hetzelfde.
Voorbeeld optellen:
2/4 + 1/4 = (2 + 1) / 4 = 3/4
Voorbeeld aftrekken:
3/5 - 1/5 = (3 - 1) / 5 = 2/5
Breuken vermenigvuldigen
Het vermenigvuldigen van breuken is eigenlijk heel gemakkelijk. Je vermenigvuldigt de tellers met elkaar en de noemers met elkaar.
Voorbeeld:
1/2 * 2/3 = (1 * 2) / (2 * 3) = 2/6
Vergeet niet dat je de breuk daarna eventueel nog kunt vereenvoudigen (zie hieronder).
Breuken delen
Het delen van breuken lijkt misschien wat ingewikkelder, maar het is eigenlijk ook heel simpel. Je vermenigvuldigt de eerste breuk met het omgekeerde van de tweede breuk. Het omgekeerde van een breuk krijg je door de teller en de noemer om te wisselen.
Voorbeeld:
1/2 : 2/3 = 1/2 * 3/2 = (1 * 3) / (2 * 2) = 3/4
Breuken vereenvoudigen
Nadat je een berekening met breuken hebt uitgevoerd, is het vaak belangrijk om de breuk te vereenvoudigen. Dit betekent dat je de breuk zo klein mogelijk maakt, zonder dat de waarde verandert.
Om een breuk te vereenvoudigen, zoek je de grootste gemene deler (GGD) van de teller en de noemer. Dit is het grootste getal dat beide getallen deelt.
Voorbeeld:
Vereenvoudig 2/6.
- De teller is 2, de noemer is 6.
- De GGD van 2 en 6 is 2.
- Deel de teller en de noemer door 2: (2 / 2) / (6 / 2) = 1/3
- De vereenvoudigde breuk is 1/3.
Van onechte breuk naar gemengd getal en vice versa
Soms wil je een onechte breuk omzetten naar een gemengd getal of andersom. Laten we eens kijken hoe dat werkt.
Van onechte breuk naar gemengd getal
Voorbeeld: Zet 7/3 om in een gemengd getal.
- Deel de teller (7) door de noemer (3): 7 : 3 = 2 met een rest van 1.
- Het gehele getal is 2.
- De rest (1) wordt de nieuwe teller.
- De noemer (3) blijft hetzelfde.
- Het gemengde getal is 2 1/3.
Van gemengd getal naar onechte breuk
Voorbeeld: Zet 3 1/4 om in een onechte breuk.
- Vermenigvuldig het gehele getal (3) met de noemer (4): 3 * 4 = 12.
- Tel de teller (1) erbij op: 12 + 1 = 13.
- Dit wordt de nieuwe teller.
- De noemer (4) blijft hetzelfde.
- De onechte breuk is 13/4.
Waarom zijn breuken belangrijk?
Breuken zijn overal om ons heen, ook al realiseer je het je misschien niet altijd. Hier zijn een paar voorbeelden:
- Koken en bakken: Recepten maken vaak gebruik van breuken om ingrediënten af te meten.
- Tijdsmeting: Een kwartier is 1/4 van een uur.
- Muziek: Noten hebben waarden die als breuken worden weergegeven (bijvoorbeeld een halve noot, een kwartnoot).
- Bouwkunde: Het berekenen van verhoudingen en schalen vereist kennis van breuken.
- Financiën: Het berekenen van rente en kortingen maakt gebruik van breuken.
Door een goed begrip van breuken ontwikkel je essentiële vaardigheden die je in je dagelijks leven kunt toepassen.
Tips voor het leren en oefenen met breuken
Breuken leren is als een spier trainen: hoe meer je oefent, hoe sterker je wordt. Hier zijn een paar tips om je te helpen:
- Begin met de basis: Zorg dat je de definitie en de verschillende soorten breuken goed begrijpt.
- Gebruik visuele hulpmiddelen: Teken cirkels, rechthoeken of pizzapunten om breuken te visualiseren.
- Oefen regelmatig: Maak oefenopgaven online of in een wiskundeboek.
- Gebruik breuken in het dagelijks leven: Meet ingrediënten af met behulp van breuken, verdeel een pizza in gelijke stukken, of bereken de korting op een artikel.
- Wees niet bang om fouten te maken: Fouten maken is een onderdeel van het leerproces. Leer van je fouten en probeer het opnieuw.
- Zoek hulp als je er niet uitkomt: Vraag je leraar, een klasgenoot of een familielid om hulp.
Conclusie
Breuken zijn een fundamenteel onderdeel van de wiskunde en spelen een cruciale rol in ons dagelijks leven. Door de basisprincipes te begrijpen en regelmatig te oefenen, kun je je wiskundige vaardigheden verbeteren en meer zelfvertrouwen krijgen in het oplossen van problemen. We hopen dat dit artikel je geholpen heeft om breuken beter te begrijpen en dat je je nu klaar voelt om ze met succes toe te passen! Nu kun je met een gerust hart dat recept volgen, die pizza eerlijk verdelen, en je wiskundige uitdagingen met een glimlach tegemoet treden.

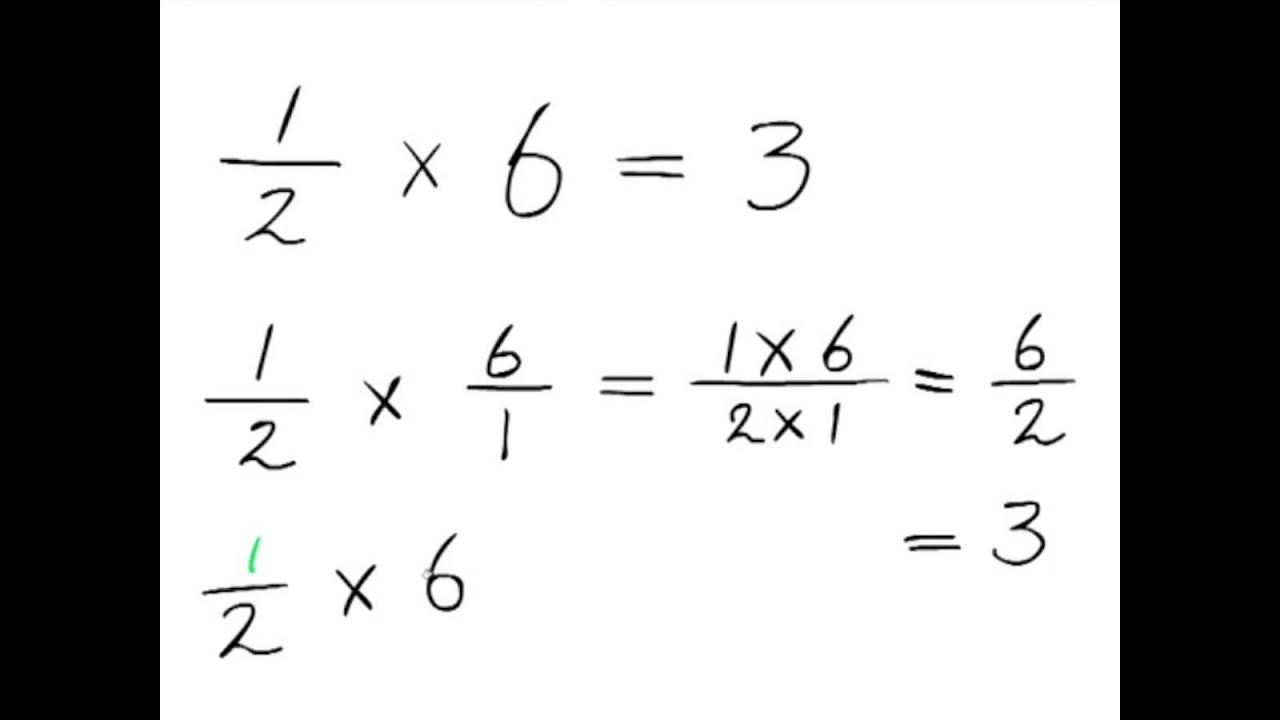
Bekijk ook deze gerelateerde berichten:
- Waar Ligt Het Noorden Van Nederland
- Met 1 Kruk Lopen Welke Kant
- Wat Is De Functie Van De Slokdarm
- Hoeveel Keer Bidden Moslims Per Dag
- Welke Amerikaanse President Volgde In 45 Roosevelt Op
- Wat Is De Omtrek Van De Aarde
- Opbouw Van Een Zakelijke Brief
- Hoeveel Belasting Betaal Je In Nederland
- Wat Voor Cijfer Moet Ik Halen
- Bloedgroepen Die Niet Samen Gaan Zwangerschap
