Hoe Bereken Je Een Driehoek

Heb je je ooit afgevraagd hoe je de oppervlakte van een driehoek kunt berekenen, of hoe je de lengte van een onbekende zijde kunt vinden? Misschien zit je vast met een wiskundeopgave, of heb je het nodig voor een project? Maak je geen zorgen, je bent niet de enige! Veel mensen vinden driehoeken in eerste instantie lastig, maar met de juiste uitleg en een paar handige formules, is het eigenlijk best eenvoudig. Deze gids loodst je stap voor stap door de verschillende manieren om een driehoek te berekenen, zodat je straks zelfverzekerd aan de slag kunt.

Oppervlakte Berekenen: De Basis

Laten we beginnen met de basis: de oppervlakte van een driehoek. De meest bekende formule hiervoor is waarschijnlijk: oppervlakte = ½ * basis * hoogte.

Maar wat betekent dat precies?

De basis is een van de zijden van de driehoek. Meestal kiezen we de zijde die horizontaal ligt, maar het kan elke zijde zijn. De hoogte is de loodrechte afstand van de basis tot de tegenoverliggende hoekpunt. Belangrijk: de hoogte staat altijd loodrecht (in een hoek van 90 graden) op de basis.

Voorbeeld: Stel je voor, een driehoek met een basis van 8 cm en een hoogte van 5 cm. De oppervlakte bereken je dan als volgt: ½ * 8 cm * 5 cm = 20 cm². Dus de oppervlakte van de driehoek is 20 vierkante centimeter.

Let op: Zorg ervoor dat je de juiste eenheden gebruikt. Als de basis in centimeters is en de hoogte in meters, moet je eerst alles naar dezelfde eenheid omrekenen voordat je de formule toepast.

Wanneer de Hoogte Niet Gegeven is: De Formule van Heron

Soms is de hoogte van een driehoek niet direct bekend. Geen probleem! Dan kun je de formule van Heron gebruiken. Deze formule is handig als je de lengtes van alle drie de zijden (a, b en c) kent.

De formule van Heron ziet er als volgt uit: oppervlakte = √[s(s-a)(s-b)(s-c)], waarbij s de halve omtrek van de driehoek is. De halve omtrek bereken je als: s = (a + b + c) / 2.

Voorbeeld: Stel, een driehoek heeft zijden van 5 cm, 7 cm en 8 cm. Eerst berekenen we de halve omtrek: s = (5 + 7 + 8) / 2 = 10 cm. Nu kunnen we de formule van Heron toepassen: oppervlakte = √[10(10-5)(10-7)(10-8)] = √(10 * 5 * 3 * 2) = √300 ≈ 17.32 cm². De oppervlakte is dus ongeveer 17.32 vierkante centimeter.

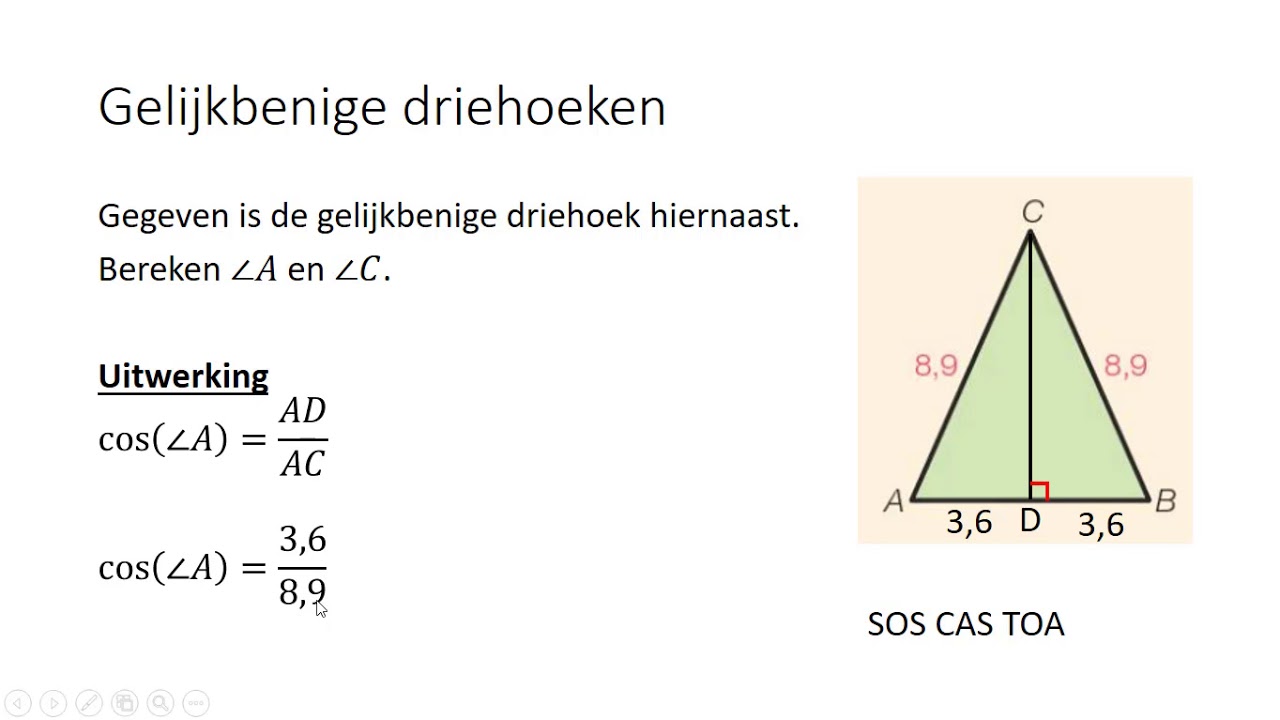
Zijden en Hoeken Berekenen: Goniometrie

Nu gaan we een stap verder: het berekenen van zijden en hoeken. Hier komt goniometrie om de hoek kijken (pun intended!). Goniometrie is de tak van de wiskunde die zich bezighoudt met de relaties tussen de zijden en hoeken van driehoeken, in het bijzonder rechthoekige driehoeken.

De Basis: Sinus, Cosinus en Tangens

De belangrijkste functies in de goniometrie zijn sinus (sin), cosinus (cos) en tangens (tan). Deze functies beschrijven de verhouding tussen de zijden van een rechthoekige driehoek en de hoeken.

Onthoud de volgende definities (SOH CAH TOA):

Sinus (sin): Overstaande zijde / Schuine zijde (SOH)
Cosinus (cos): Aanliggende zijde / Schuine zijde (CAH)
Tangens (tan): Overstaande zijde / Aanliggende zijde (TOA)

Hierbij is de overstaande zijde de zijde tegenover de hoek die je bekijkt, de aanliggende zijde is de zijde die aan de hoek grenst (maar niet de schuine zijde), en de schuine zijde is de langste zijde van de rechthoekige driehoek (tegenover de rechte hoek).

Voorbeeld: Stel, je hebt een rechthoekige driehoek met een hoek van 30 graden. De schuine zijde is 10 cm lang. Je wilt de lengte van de overstaande zijde berekenen. Je gebruikt de sinus-functie: sin(30°) = overstaande zijde / 10 cm. Aangezien sin(30°) = 0.5, geldt: 0.5 = overstaande zijde / 10 cm. Dus de overstaande zijde = 0.5 * 10 cm = 5 cm.

De Stelling van Pythagoras

Een andere belangrijke stelling, vooral voor rechthoekige driehoeken, is de stelling van Pythagoras. Deze stelling stelt dat in een rechthoekige driehoek het kwadraat van de schuine zijde gelijk is aan de som van de kwadraten van de andere twee zijden: a² + b² = c², waarbij a en b de lengtes van de rechthoekszijden zijn en c de lengte van de schuine zijde.

Voorbeeld: Stel, een rechthoekige driehoek heeft zijden van 3 cm en 4 cm. Je wilt de lengte van de schuine zijde berekenen. Dan geldt: 3² + 4² = c². Dus 9 + 16 = c², wat betekent dat c² = 25. Dus c = √25 = 5 cm. De schuine zijde is dus 5 cm lang.

De Sinusregel en Cosinusregel

Voor driehoeken die *niet* rechthoekig zijn, gebruiken we de sinusregel en de cosinusregel. Deze regels stellen ons in staat om zijden en hoeken te berekenen, zelfs als we geen rechte hoek hebben.

Sinusregel: a / sin(A) = b / sin(B) = c / sin(C), waarbij a, b en c de lengtes van de zijden zijn en A, B en C de hoeken tegenover die zijden.

Cosinusregel: c² = a² + b² - 2ab * cos(C), waarbij c de zijde is tegenover hoek C.

De sinusregel is handig als je twee hoeken en een zijde kent, of twee zijden en de hoek tegenover een van die zijden. De cosinusregel is handig als je drie zijden kent, of twee zijden en de ingesloten hoek (de hoek tussen die twee zijden).

Voorbeeld Sinusregel: Stel, je hebt een driehoek met hoeken A = 40°, B = 60° en zijde a = 8 cm. Je wilt zijde b berekenen. Met de sinusregel: 8 / sin(40°) = b / sin(60°). Dus b = (8 * sin(60°)) / sin(40°) ≈ (8 * 0.866) / 0.643 ≈ 10.77 cm.

Voorbeeld Cosinusregel: Stel, je hebt een driehoek met zijden a = 5 cm, b = 7 cm en hoek C = 45°. Je wilt zijde c berekenen. Met de cosinusregel: c² = 5² + 7² - 2 * 5 * 7 * cos(45°) = 25 + 49 - 70 * 0.707 ≈ 74 - 49.49 ≈ 24.51. Dus c = √24.51 ≈ 4.95 cm.

Praktische Toepassingen

Het berekenen van driehoeken is niet alleen handig voor wiskundeopgaven. Het komt in veel praktische situaties van pas:

Architectuur: Voor het ontwerpen van gebouwen en bruggen.
Navigatie: Voor het bepalen van afstanden en richtingen.
Landmeten: Voor het in kaart brengen van land.
Engineering: Voor het ontwerpen van machines en constructies.
Spellen: Voor het berekenen van botsingen en afstanden in games.

Tips en Tricks

* Schets de driehoek: Maak altijd een schets van de driehoek, zelfs als het niet verplicht is. Dit helpt je om de situatie te visualiseren en de juiste formules te kiezen. * Label de zijden en hoeken: Label de zijden en hoeken duidelijk, zodat je geen fouten maakt bij het invullen van de formules. * Gebruik de juiste eenheden: Zorg ervoor dat je alle afmetingen in dezelfde eenheden hebt (bijvoorbeeld allemaal in centimeters of allemaal in meters). * Controleer je antwoord: Controleer je antwoord om te zien of het logisch is. Een negatieve lengte of een hoek groter dan 180 graden is onmogelijk. * Oefening baart kunst: Hoe meer je oefent met het berekenen van driehoeken, hoe beter je erin wordt. Probeer verschillende soorten opgaven en daag jezelf uit. * Gebruik een rekenmachine: Een wetenschappelijke rekenmachine is essentieel voor het berekenen van goniometrische functies. Zorg ervoor dat je weet hoe je deze functies op je rekenmachine kunt vinden en gebruiken.

Conclusie: Het berekenen van driehoeken kan in eerste instantie lastig lijken, maar met een beetje oefening en de juiste formules, kan iedereen het leren. Onthoud de basisformules voor oppervlakte, de formule van Heron, de stelling van Pythagoras, de sinusregel en de cosinusregel. En vergeet niet om een schets te maken en je antwoord te controleren! Veel succes!