Hoe Bereken Je Het Startgetal
Heb je je ooit afgevraagd hoe je dat magische startgetal in een lineaire vergelijking kunt vinden? Of je nu een student bent die worstelt met wiskunde, een leraar die een duidelijke uitleg zoekt, of gewoon iemand met interesse in numerieke puzzels, dit artikel is voor jou. We gaan diep in op de methoden om het startgetal te berekenen, en we maken het begrijpelijk en toepasbaar in de praktijk.
Wat is het Startgetal Eigenlijk?
Het startgetal, ook wel het y-intercept genoemd, is een cruciaal onderdeel van een lineaire vergelijking. Het vertegenwoordigt het punt waar de lijn de y-as kruist. Simpel gezegd, het is de waarde van y wanneer x gelijk is aan 0. Denk aan het als het beginpunt van je grafiek, het vertrekpunt voordat de lijn begint te stijgen of dalen.
Waarom is het Startgetal Belangrijk?
Het startgetal is belangrijk om verschillende redenen:
- Begrip van de context: Het geeft vaak een betekenisvolle beginwaarde in een real-world situatie. Denk bijvoorbeeld aan de beginwaarde van een spaarrekening of de temperatuur op een bepaald moment.
- Grafische representatie: Het helpt je de grafiek van een lineaire functie correct te tekenen. Je weet waar de lijn de y-as snijdt.
- Vergelijkingen oplossen: Het is een essentieel onderdeel van het oplossen van lineaire vergelijkingen.
Methoden om het Startgetal te Berekenen
Er zijn verschillende manieren om het startgetal te berekenen, afhankelijk van de informatie die je hebt. We bespreken de meest voorkomende methoden.
1. Vanuit de Vergelijking (y = mx + b)
De meest directe manier is om het startgetal te vinden als je de vergelijking van de lijn al hebt in de vorm y = mx + b. Hierin staat:
- y voor de afhankelijke variabele (de y-waarde)
- x voor de onafhankelijke variabele (de x-waarde)
- m voor de helling (de richtingscoëfficiënt)
- b voor het startgetal (de y-intercept)
Het startgetal is dus eenvoudigweg de waarde van b in de vergelijking.
Voorbeeld:
Stel dat je de vergelijking y = 2x + 3 hebt. Het startgetal is hier 3. Dit betekent dat de lijn de y-as snijdt bij y = 3.
2. Vanuit een Grafiek
Als je een grafiek van de lijn hebt, kun je het startgetal vinden door te kijken naar het punt waar de lijn de y-as snijdt. Dit is de y-coördinaat van dat snijpunt.
Voorbeeld:
Als de lijn de y-as snijdt bij het punt (0, -2), dan is het startgetal -2.
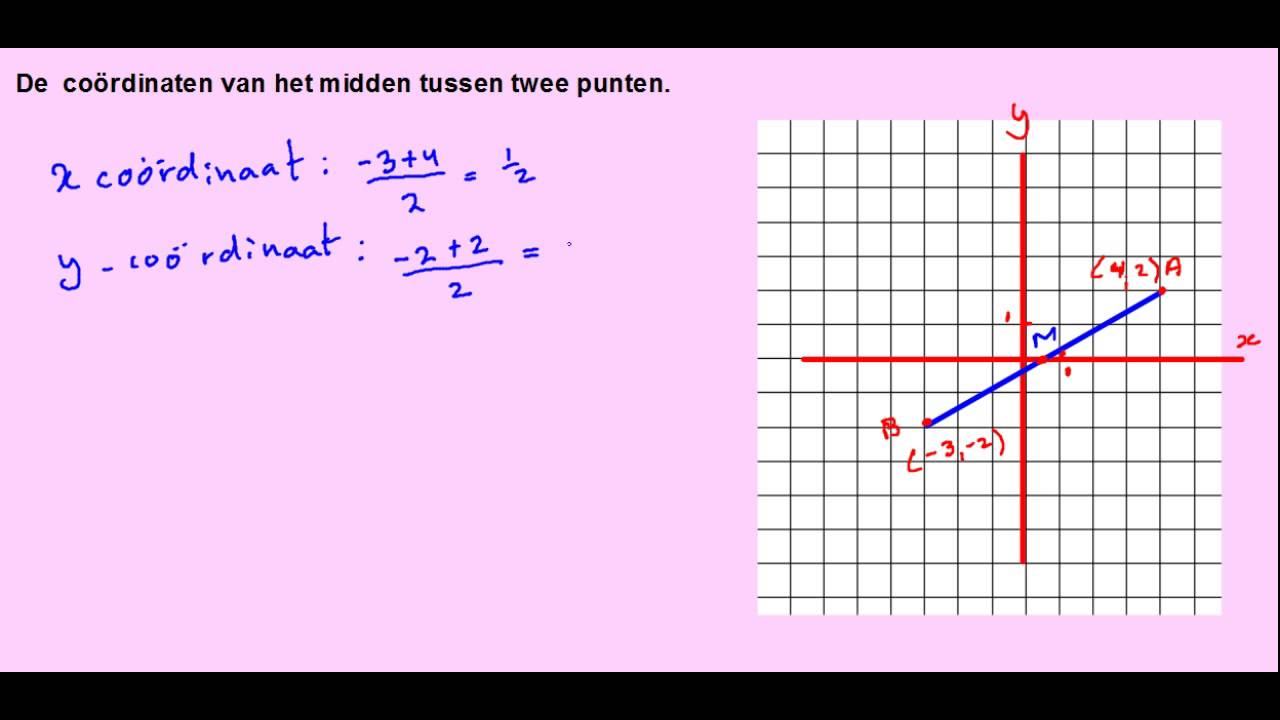
3. Vanuit Twee Punten
Soms heb je alleen twee punten op de lijn, bijvoorbeeld (x₁, y₁) en (x₂, y₂). In dat geval kun je het startgetal als volgt berekenen:
- Bereken de helling (m): De helling wordt berekend met de formule: m = (y₂ - y₁) / (x₂ - x₁)
- Gebruik de punt-helling vorm: Kies een van de twee punten (bijvoorbeeld (x₁, y₁)) en vul de helling en het punt in in de punt-helling vorm van de lineaire vergelijking: y - y₁ = m(x - x₁)
- Herschrijf naar de vorm y = mx + b: Vereenvoudig de vergelijking om deze in de vorm y = mx + b te krijgen. De waarde van 'b' is dan het startgetal.
Voorbeeld:
Stel dat je de punten (1, 5) en (3, 9) hebt.
- Bereken de helling: m = (9 - 5) / (3 - 1) = 4 / 2 = 2
- Gebruik de punt-helling vorm: y - 5 = 2(x - 1)
- Herschrijf naar de vorm y = mx + b: y - 5 = 2x - 2 => y = 2x + 3. Het startgetal is dus 3.
4. Vanuit een Tabel met Waarden
Als je een tabel met x- en y-waarden hebt, kun je het startgetal vinden door te kijken naar de y-waarde die overeenkomt met x = 0. Als de tabel geen waarde voor x = 0 bevat, kun je een lineaire extrapolatie uitvoeren om de y-waarde te schatten wanneer x = 0.
Voorbeeld:
Stel dat je de volgende tabel hebt:
| x | y |
|---|---|
| 1 | 4 |
| 2 | 6 |
De helling is (6-4)/(2-1) = 2. Als we de helling en het punt (1, 4) gebruiken, kunnen we de vergelijking vinden: y - 4 = 2(x - 1). Dit leidt tot y = 2x + 2. Het startgetal is dus 2.
Praktische Toepassingen
Het berekenen van het startgetal is niet alleen een wiskundige oefening. Het heeft veel praktische toepassingen in het dagelijks leven en in verschillende vakgebieden.
- Financiën: Bij het berekenen van spaargeld, kan het startgetal je begininleg zijn. De helling vertegenwoordigt dan de rentevoet.
- Natuurkunde: Bij het bestuderen van beweging, kan het startgetal de beginpositie van een object zijn. De helling vertegenwoordigt dan de snelheid.
- Economie: Bij het analyseren van vraag en aanbod, kan het startgetal de autonome consumptie zijn. Dit is de consumptie die plaatsvindt, zelfs als er geen inkomen is.
- Computerwetenschappen: Bij lineaire regressie in machine learning, is het startgetal een belangrijk parameter in het model.
Tips en Tricks voor het Berekenen van het Startgetal
Hier zijn een paar handige tips en tricks om het berekenen van het startgetal makkelijker te maken:
- Visualiseer de lijn: Probeer altijd de lijn voor te stellen in je hoofd. Dit helpt je te begrijpen wat het startgetal representeert.
- Controleer je antwoord: Nadat je het startgetal hebt berekend, controleer of het logisch is in de context van het probleem.
- Gebruik grafische rekenmachines: Grafische rekenmachines kunnen helpen bij het visualiseren van lijnen en het vinden van het snijpunt met de y-as.
- Oefening baart kunst: Hoe meer je oefent met het berekenen van het startgetal, hoe sneller en accurater je zult worden.
Veelgemaakte Fouten en Hoe Ze Te Vermijden
Het is gemakkelijk om fouten te maken bij het berekenen van het startgetal. Hier zijn enkele veelgemaakte fouten en hoe je ze kunt vermijden:
- Verkeerde formule gebruiken: Zorg ervoor dat je de juiste formule gebruikt voor de methode die je toepast.
- Helling verkeerd berekenen: Een veelvoorkomende fout is het omwisselen van de x- en y-waarden bij het berekenen van de helling.
- Verkeerde punten selecteren: Zorg ervoor dat je de juiste punten selecteert uit de grafiek of tabel.
- Negatieve tekens vergeten: Let goed op de negatieve tekens, vooral bij het berekenen van de helling.
Conclusie: Start je Begrip van Lineaire Functies met een Sterke Basis
Het berekenen van het startgetal is een fundamentele vaardigheid in de wiskunde en heeft vele praktische toepassingen. Door de verschillende methoden te begrijpen en te oefenen, kun je je begrip van lineaire functies verbeteren en problemen effectiever oplossen. Of je nu een student bent die worstelt met wiskunde, een leraar die een duidelijke uitleg zoekt, of gewoon iemand met interesse in numerieke puzzels, begrijp het startgetal en je staat steviger in je schoenen. Wees niet bang om te oefenen, vragen te stellen en de tools die tot je beschikking staan te gebruiken. Met de juiste inspanning kan iedereen het startgetal leren berekenen en de schoonheid en bruikbaarheid van lineaire functies waarderen.
Bekijk ook deze gerelateerde berichten:
- Hoe Kan Je De Persoonsvorm Vinden
- Hoelang Is Een Theorie Examen Geldig
- Wat Is De Afkorting Van Glucose
- N Term Engels Havo Afgelopen Jaren
- Hoe Begin Je Een Brief In Het Engels
- Mag Een Winkelier Contant Geld Weigeren
- 50 Gram Is Hoeveel Ml
- Laat Niet Als Dank Voor Het Aangenaam Verpozen
- Wat Zie Je Op Rontgenfoto
- Voet Aan De Grond Krijgen
