Hoe Bereken Je Het Volume

Heb je je ooit afgevraagd hoe je de hoeveelheid water in een zwembad berekent, de hoeveelheid zand die je nodig hebt voor een zandbak, of zelfs de inhoud van een doos voor je verhuizing? Het berekenen van volume kan intimiderend lijken, vooral als wiskunde niet je sterkste punt is. Maar vrees niet! Dit artikel is bedoeld om je te helpen de basisprincipes van volumeberekening te begrijpen, zodat je deze vaardigheid in verschillende situaties kunt toepassen.

Waarom is het Berekenen van Volume Belangrijk?

Het berekenen van volume is niet zomaar een abstracte wiskundige oefening. Het heeft veel praktische toepassingen in het dagelijks leven. Denk eens aan:

Klussen in huis: Of je nu beton moet mengen voor een terras, aarde nodig hebt voor een bloembed, of wilt weten hoeveel verf je moet kopen voor een kamer, volumeberekening is essentieel.
Koken en bakken: Recepten vereisen vaak nauwkeurige metingen, en het begrijpen van volume kan je helpen om ingrediënten correct om te zetten.
Verhuizen: Het inschatten van het volume van je bezittingen helpt bij het kiezen van de juiste maat verhuiswagen en het bepalen van de kosten.
Aquarium: Om ervoor te zorgen dat je vissen genoeg ruimte hebben om te leven en de juiste hoeveelheid waterbehandeling toe te voegen is volumeberekening cruciaal.
Professionele toepassingen: Architecten, ingenieurs en ontwerpers gebruiken volumeberekeningen constant in hun werk, van het ontwerpen van gebouwen tot het bepalen van de capaciteit van reservoirs.

Kortom, het begrijpen van volume stelt je in staat om nauwkeurige schattingen te maken, kosten te besparen en problemen efficiënter op te lossen. Het is een skill die je waarschijnlijk vaker nodig hebt dan je denkt!

De Basisformules: Simpel Uitgelegd

Laten we eens kijken naar de formules voor het berekenen van het volume van enkele veelvoorkomende vormen:

Kubus

Een kubus is een driedimensionale vorm met zes gelijke vierkante vlakken. De formule voor het volume van een kubus is:

Volume = zijde x zijde x zijde = zijde³

Voorbeeld: Stel dat een kubus een zijde heeft van 5 cm. Het volume is dan 5 cm x 5 cm x 5 cm = 125 cm³.

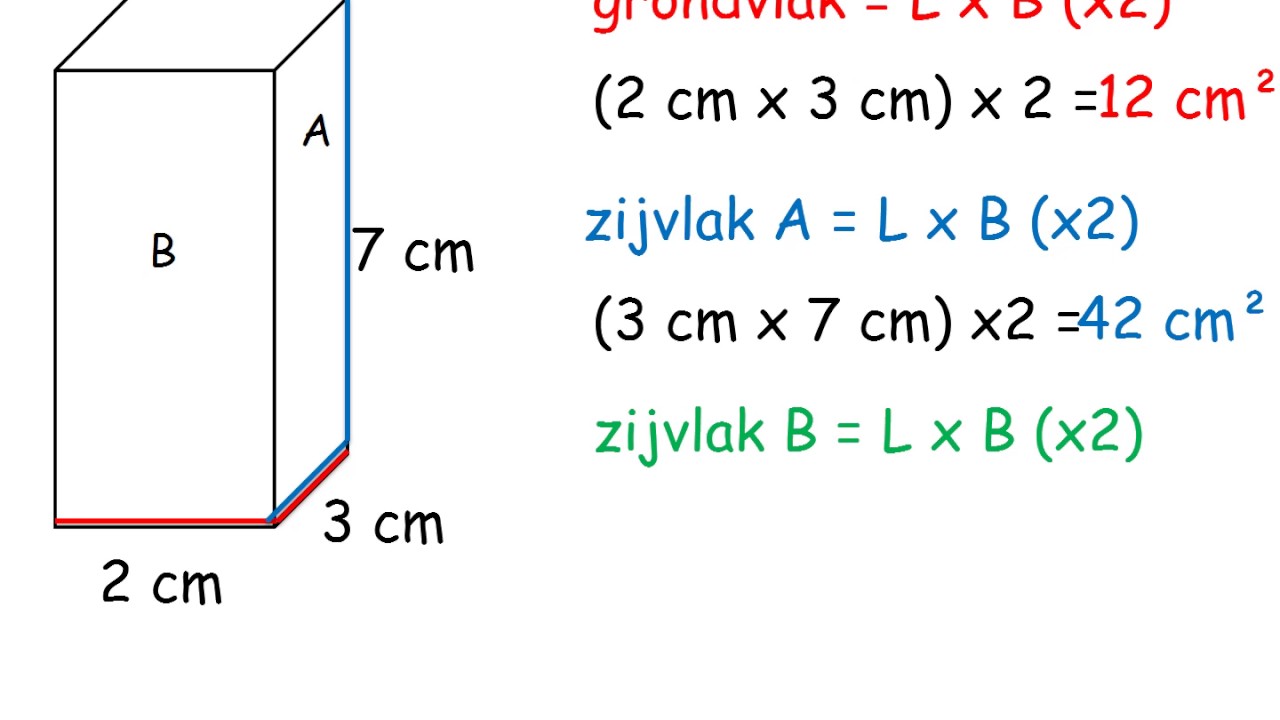
Rechthoekig Prisma (Balk)

Een rechthoekig prisma, ook wel een balk genoemd, heeft zes rechthoekige vlakken. De formule voor het volume is:

Volume = lengte x breedte x hoogte

Voorbeeld: Stel dat een balk een lengte heeft van 8 cm, een breedte van 4 cm en een hoogte van 3 cm. Het volume is dan 8 cm x 4 cm x 3 cm = 96 cm³.

Cilinder

Een cilinder heeft twee cirkelvormige vlakken en een gebogen oppervlak. De formule voor het volume is:

Volume = π x straal² x hoogte

Waarbij π (pi) ongeveer 3.14159 is, de straal de helft van de diameter van de cirkel is, en de hoogte de afstand tussen de twee cirkelvormige vlakken is.

Voorbeeld: Stel dat een cilinder een straal heeft van 2 cm en een hoogte van 10 cm. Het volume is dan 3.14159 x 2 cm x 2 cm x 10 cm = 125.66 cm³ (ongeveer).

Kegel

Een kegel heeft een cirkelvormige basis en loopt taps toe naar een punt. De formule voor het volume is:

Volume = (1/3) x π x straal² x hoogte

Voorbeeld: Stel dat een kegel een straal heeft van 3 cm en een hoogte van 6 cm. Het volume is dan (1/3) x 3.14159 x 3 cm x 3 cm x 6 cm = 56.55 cm³ (ongeveer).

Bol

Een bol is een perfect ronde driedimensionale vorm. De formule voor het volume is:

Volume = (4/3) x π x straal³

Voorbeeld: Stel dat een bol een straal heeft van 4 cm. Het volume is dan (4/3) x 3.14159 x 4 cm x 4 cm x 4 cm = 268.08 cm³ (ongeveer).

Omgaan met Complexe Vormen

Wat als je te maken hebt met een vorm die niet een eenvoudige kubus, balk, cilinder, kegel of bol is? Hier zijn enkele strategieën:

Verdeel de vorm: Probeer de complexe vorm op te splitsen in eenvoudiger, herkenbare vormen waarvan je het volume wel kunt berekenen. Tel vervolgens de volumes van de afzonderlijke delen bij elkaar op.
Gebruik verplaatsing (methode van Archimedes): Dompel het object onder in een bak met water. Meet de hoeveelheid water die wordt verplaatst. Het volume van het verplaatste water is gelijk aan het volume van het object. Dit werkt bijzonder goed voor onregelmatige vormen.
Online rekenmachines: Er zijn tal van online volume rekenmachines beschikbaar voor complexere vormen. Zoek bijvoorbeeld naar rekenmachines voor afgeknotte kegels, prisma's met onregelmatige basisvormen, etc.

Een Analogie: Stel je voor dat je het volume van een huis wilt berekenen. Je kunt het huis verdelen in een rechthoekig prisma (de basis) en een driehoekig prisma (het dak). Bereken het volume van elk prisma afzonderlijk en tel ze vervolgens bij elkaar op.

Veelgemaakte Fouten en Hoe ze te Vermijden

Bij het berekenen van volume kunnen er fouten optreden. Hier zijn enkele veelvoorkomende valkuilen en hoe je ze kunt vermijden:

Verkeerde eenheden: Zorg ervoor dat alle metingen in dezelfde eenheden zijn (bijvoorbeeld allemaal in centimeters, meters, of inches) voordat je gaat rekenen. Als je verschillende eenheden hebt, converteer ze dan eerst.
Verkeerde formule: Gebruik de juiste formule voor de vorm die je aan het berekenen bent. Dubbelcheck je formule!
Rekenfouten: Wees voorzichtig bij het uitvoeren van de berekeningen. Gebruik een rekenmachine als je het niet zeker weet.
Vergeet niet eenheden te vermelden: Zorg ervoor dat je de eenheid vermeldt bij je eindantwoord (bijvoorbeeld cm³, m³, of liters). Een getal zonder eenheid heeft geen betekenis in de context van volume.
Afrondingsfouten: Vermijd het afronden van tussenresultaten. Rond pas af bij het eindantwoord om de nauwkeurigheid te waarborgen.

Tegenargumenten en Nuancering

Sommigen beweren dat in de moderne wereld met geavanceerde technologie het handmatig berekenen van volume overbodig is geworden. Immers, er zijn apps en software die dit in een oogwenk kunnen doen. Hoewel dit waar is, is het belangrijk om te begrijpen hoe deze apps en software werken. Het begrijpen van de basisprincipes van volumeberekening stelt je in staat om de resultaten van deze tools te beoordelen op juistheid en om te gaan met situaties waarin je geen toegang hebt tot technologie.

Daarnaast helpt het je probleemoplossend te denken. Stel dat een machine een verkeerd volume berekent, zonder kennis van de basis kan je dit niet controleren en herstellen.

Van Theorie naar Praktijk: Voorbeelden

Laten we eens kijken naar enkele praktische voorbeelden:

Een zwembad vullen: Je wilt een rechthoekig zwembad vullen dat 10 meter lang, 5 meter breed en 2 meter diep is. Het volume is 10 m x 5 m x 2 m = 100 m³. Je moet dus 100.000 liter water gebruiken (1 m³ = 1000 liter).
Zand voor een zandbak: Je hebt een ronde zandbak met een diameter van 2 meter en je wilt deze vullen tot een hoogte van 30 cm (0,3 meter). De straal is 1 meter. Het volume is π x 1 m² x 0.3 m = 0.94 m³ (ongeveer).
Verf voor een kamer: Je wilt een kamer verven die 4 meter lang, 3 meter breed en 2.5 meter hoog is. De totale oppervlakte van de muren is 2 x (4 m x 2.5 m) + 2 x (3 m x 2.5 m) = 35 m². Als één liter verf 10 m² bedekt, heb je 3.5 liter verf nodig (waarschijnlijk 4 liter, om zeker te zijn).

Conclusie

Het berekenen van volume is een waardevolle vaardigheid die je in talloze situaties van pas komt. Door de basisformules te begrijpen, complexere vormen te benaderen met behulp van opsplitsing of verplaatsing, en veelgemaakte fouten te vermijden, kun je zelfverzekerd het volume van objecten en ruimtes berekenen.

Hopelijk heeft dit artikel je geholpen om de basisprincipes van volumeberekening beter te begrijpen. Nu is het jouw beurt! Waar ga jij als eerste het volume van berekenen?